【HDU】4658 Integer Partition【生成函式——數拆分】
阿新 • • 發佈:2019-01-09
題目分析:
用了五邊形數定理以及生成函式,然而我看懂了生成函式怎麼搞這題卻不知道為啥生成函式是五邊形數形式= =
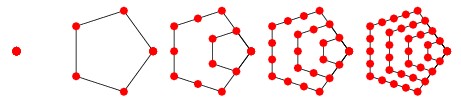
首先觀察下面的圖片:
很容易我們可以發現用這種方式構造N個五邊形(假設一個點也算一個五邊形),需要點的個數為:
接下來我們來看一下數拆分。
提問:將一個正整數
很容易我們可以構造一個多項式:
可以發現N的數拆分的方案數正對應著多項式展開後 n
考慮如下等式:
因此我們有:
其中上式等式左邊是尤拉函式
尤拉函式
其中的x的指數正對應著廣義五邊形數!
| 0 | 1 | -1 | 2 | -2 | 3 | -3 | 4 | -4 | … | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 5 | 7 | 12 | 15 | 22 | 26 | … |
現在我們要計算
所以: