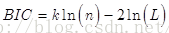此處模型選擇我們只考慮模型引數數量，不涉及模型結構的選擇。

很多引數估計問題均採用似然函式作為目標函式，當訓練資料足夠多時，可以不斷提高模型精度，但是以提高模型複雜度為代價的，同時帶來一個機器學習中非常普遍的問題——過擬合。所以，模型選擇問題在模型複雜度與模型對資料集描述能力（即似然函式）之間尋求最佳平衡。

人們提出許多資訊準則，通過加入模型複雜度的懲罰項來避免過擬合問題，此處我們介紹一下常用的兩個模型選擇方法——赤池資訊準則（Akaike Information Criterion，AIC）和貝葉斯資訊準則（Bayesian Information Criterion，BIC）。

AIC是衡量統計模型擬合優良性的一種標準，由日本統計學家赤池弘次在1974年提出，它建立在熵的概念上，提供了權衡估計模型複雜度和擬合數據優良性的標準。

通常情況下，AIC定義為：

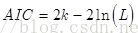
其中k是模型引數個數，L是似然函式。從一組可供選擇的模型中選擇最佳模型時，通常選擇AIC最小的模型。

當兩個模型之間存在較大差異時，差異主要體現在似然函式項，當似然函式差異不顯著時，上式第一項，即模型複雜度則起作用，從而引數個數少的模型是較好的選擇。

一般而言，當模型複雜度提高（k增大）時，似然函式L也會增大，從而使AIC變小，但是k過大時，似然函式增速減緩，導致AIC增大，模型過於複雜容易造成過擬合現象。目標是選取AIC最小的模型，AIC不僅要提高模型擬合度（極大似然），而且引入了懲罰項，使模型引數儘可能少，有助於降低過擬合的可能性。

BIC（Bayesian InformationCriterion）貝葉斯資訊準則與AIC相似，用於模型選擇，1978年由Schwarz提出。訓練模型時，增加引數數量，也就是增加模型複雜度，會增大似然函式，但是也會導致過擬合現象，針對該問題，AIC和BIC均引入了與模型引數個數相關的懲罰項，BIC的懲罰項比AIC的大，考慮了樣本數量，樣本數量過多時，可有效防止模型精度過高造成的模型複雜度過高。

其中，k為模型引數個數，n為樣本數量，L為似然函式。kln(n)懲罰項在維數過大且訓練樣本資料相對較少的情況下，可以有效避免出現維度災難現象。