看了一些別人的部落格，發現裡面涉及到的公式沒有證明，於是就打算自己寫一篇比較詳細的講解。

先看兩個引理及其證明(建議把證明搞懂)。

PS：以下圖片均為作者用wps製作，如想使用請附上作者部落格連結，謝謝O(∩_∩)O。

看完了上面的引理，那就可以正式開始Miller-Rabin演算法的講解了。

背景：

素性測試(即測試給定的數是否為素數)是近代密碼學中的一個非常重要的課題。雖然Wilson定理(對於給定的正整數n，n是素數的充要條件為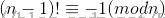)給出了一個數是素數的充要條件，但根據它來素性測試所需的計算量太大，無法實現對較大整數的測試。目前，儘管高效的確定性的素性演算法尚未找到，但已有一些隨機演算法可用於素性測試及大整數的因數分解。下面描述的

演算法：

首先要知道費馬定理只是n是素數的必要條件。即費馬定理不成立，n一定是合數；費馬定理成立，n可能是素數。接下來請看Miller-Rabin演算法的分析過程。

如果仔細看的話，應該能看懂大致原理了，數論基礎好的甚至都可以開始寫程式碼了吧，哈哈。

示例程式碼如下：

typedef long long int ll;

ll mod_mul(ll a, ll b, ll mod)
{
    ll res = 0;
    while (b)
    {
        if (b & 1)
            res = (res + a) % mod;
        a = (a + a) % mod;
        b >>= 1;
    }
    return res;
}

ll mod_pow(ll a, ll n, ll mod)
{
    ll res = 1;
    while (n)
    {
        if (n & 1)
            res = mod_mul(res, a, mod);
        a = mod_mul(a, a, mod);
        n >>= 1;
    }
    return res;
}

// Miller-Rabin隨機演算法檢測n是否為素數
bool Miller_Rabin(ll n)
{
    if (n == 2)
        return true;
    if (n < 2 || !(n & 1))
        return false;
    ll m = n - 1, k = 0;
    while (!(m & 1))
    {
        k++;
        m >>= 1;
    }
    for (int i = 1; i <= 20; i++)  // 20為Miller-Rabin測試的迭代次數
    {
        ll a = rand() % (n - 1) + 1;
        ll x = mod_pow(a, m, n);
        ll y;
        for (int j = 1; j <= k; j++)
        {
            y = mod_mul(x, x, n);
            if (y == 1 && x != 1 && x != n - 1)
                return false;
            x = y;
        }
        if (y != 1)
            return false;
    }
    return true;
}