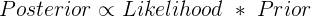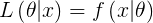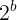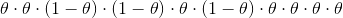EM概率統計基礎(二)
前言
前面《EM概率統計基礎(一)》簡單講解了後驗概率和先驗概率之間的關係,得到如下結果:
先驗概率乘以似然函式,正比於後驗概率
那麼 似然函式是什麼,它和概率又有什麼關係,希望可以總結總結。
似然函式
Likelihood Function
似然函式也稱為似然,是一個關於統計模型引數的函式,也就是這個函式中自變數統計模型的引數。似然函式是關於統計引數的函式,可以用來評估一組統計的引數。
似然函式的定義,它是給定聯合樣本值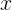

表示聯合樣本隨機變數
取到的值,即
;
是指未知引數,它屬於引數空間;
是一個密度函式,它表示(給定)
下關於聯合樣本值
的聯合密度函式
所以從定義上可以看出似然函式和密度函式完全兩個數學物件:前者是關於 
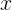
似然和概率的區別
首先給出一個簡便的區分方法,根據定義:
“xxxx的概率”中xxxx只能是概率空間中的事件,即事件(發生)的概率是多少,因為時間具有概率結構從而刻畫隨機性,所以才能談概率
“xxxx的似然”中xxxx只能是引數,比如說上文所述的引數等於
舉個栗子:
已知一個硬幣是均勻的(在拋的過程中,正反面的概率相等),那連續10次正面朝上的概率是多少,這是一個概率問題。
如果一個硬幣在10次拋落中均正面朝上,那硬幣的是均勻的(在拋落中,正反面的概率相等)概率是多少,此時的概率是似然。
Probability is used before data are available to describe possible future outcomes given a fixed value for the parameter (or parameter vector).
Likelihood is used after data are available to describe a function of a parameter (or parameter vector) for a given outcome.
The likelihood of a set of parameter values, θ, given outcomes x, is equal to the probability of those observed outcomes given those parameter values, that is
有趣的栗子
這個栗子摘自Quora上一個計算機系教授的回答,很有意思。
其將概率密度函式和似然函式之間類比成 與
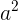
假設一個函式為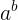
如果設定b = 2,那麼可以得到一個關於a的二次函式,即
如果設定為a = 2 ,那麼將得到一個指數函式,即

可以看出,這兩個函式雖然有著不同的名字,但源自於同一個函式
同樣的,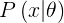

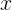
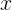

以下舉一個栗子(沒錯,我超喜歡吃栗子的)
有一個硬幣,它有 



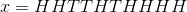
通過概率論基礎我們可以得出,出現此序列的概率為:
我們嘗試了所有

這個曲線就是

如圖所示,最可能的假設是,但實際上這個實驗量太小,無法稅負你這個硬幣是均質的,但0.7就是最大似然估計,只是因為樣本太少而導致最大似然值偏差過大,如果擴充樣本空間,H和T的樣本數量將趨近於1:1,那最終求得的最大似然估計將接近0.5.
總結
常說的概率指的是給定引數後,預測即將發生的事件的可能性,而似然概率則正好相反,我們關注的量不再是時間的發生概率,而是已知發生了某些事件,我們希望知道引數應該是多少。最大似然概率就是在已知觀測資料的前提下,找到使得似然概率最大的引數值。
此篇只是簡單介紹了下似然函式和概率之間的區別,下篇希望總結一下極大似然估計(MLE)和極大後驗估計(MAP),如果有什麼錯誤,歡迎大佬們批評指正。