1.桶排序(Bucket Sort)

基本思路是：

1.  將待排序元素劃分到不同的痛。先掃描一遍序列求出最大值 maxV 和最小值 minV ，設桶的個數為 k ，則把區間 [minV, maxV] 均勻劃分成 k 個區間，每個區間就是一個桶。將序列中的元素分配到各自的桶。
2. 對每個桶內的元素進行排序。可以選擇任意一種排序演算法。
3.  將各個桶中的元素合併成一個大的有序序列。
4. 假設資料是均勻分佈的，則每個桶的元素平均個數為 n/k 。假設選擇用快速排序對每個桶內的元素進行排序，那麼每次排序的時間複雜度為 O(n/klog(n/k)) 。總的時間複雜度為 O(n)+O(m)O(n/klog(n/k)) = O(n+nlog(n/k)) = O(n+nlogn-nlogk 。當 k 接近於 n 時，桶排序的時間複雜度就可以金斯認為是 O(n) 的。即桶越多，時間效率就越高，而桶越多，空間就越大。

2.計數排序(Counting Sort)

是一種O(n)的排序演算法，其思路是開一個長度為 maxValue-minValue+1 的陣列，然後

1. 分配。掃描一遍原始陣列，以當前值- minValue 作為下標，將該下標的計數器增1。
2. 收集。掃描一遍計數器陣列，按順序把值收集起來。

舉個例子， nums=[2, 1, 3, 1, 5] , 首先掃描一遍獲取最小值和最大值， maxValue=5 , minValue=1 ，於是開一個長度為5的計數器陣列 counter ，
1. 分配。統計每個元素出現的頻率，得到 counter=[2, 1, 1, 0, 1] ，例如 counter[0] 表示值 0+minValue=1 出現了2次。
2. 收集。 counter[0]=2 表示 1 出現了兩次，那就向原始陣列寫入兩個1， counter[1]=1 表示 2 出現了1次，那就向原始陣列寫入一個2，依次類推，最終原始陣列變為 [1,1,2,3,5] ，排序好了。

計數排序本質上是一種特殊的桶排序，當桶的個數最大的時候，就是計數排序。

3.基數排序

是一種非比較排序演算法，時間複雜度是 O(n) 。它的主要思路是，
1. 將所有待排序整數（注意，必須是非負整數）統一為位數相同的整數，位數較少的前面補零。一般用10進位制，也可以用16進位制甚至2進位制。所以前提是能夠找到最大值，得到最長的位數，設 k 進位制下最長為位數為 d 。
2. 從最低位開始，依次進行一次穩定排序。這樣從最低位一直到最高位排序完成以後，整個序列就變成了一個有序序列。
舉個例子，有一個整數序列，0, 123, 45, 386, 106，下面是排序過程：

1. 第一次排序，個位，000 123 045 386 106，無任何變化
2. 第二次排序，十位，000 106 123 045 386
3. 第三次排序，百位，000 045 106 123 386
4. 最終結果，0, 45, 106, 123, 386, 排序完成。

• 為什麼同一數位的排序子程式要用穩定排序？因為穩定排序能將上一次排序的成果保留下來。例如十位數的排序過程能保留個位數的排序成果，百位數的排序過程能保留十位數的排序成果。能不能用2進位制？能，可以把待排序序列中的每個整數都看成是01組成的二進位制數值。那這樣的話，豈不是任意一個非負整數序列都可以用基數排序演算法？理論上是的，假設待排序序列中最大整數為2 4 . 1，則最大位數 d=64 ，時間複雜度為 O(64n) 。可見任意一個非負整數序列都可以線上性時間內完成排序。
• 既然任意一個非負整數序列都可以線上性時間內完成排序，那麼基於比較排序的演算法有什麼意義呢？基於比較的排序演算法，時間複雜度是 O(nlogn) ，看起來比 O(64n) 慢，仔細一想，其實不是， O(nlogn) 只有當序列非常長，達到2 個元素的時候，才會與 O(64n) 相等，因此，64這個常數係數太大了，大部分時候， n 遠遠小於2 ，基於比較的排序演算法還是比 O(64n) 快的。
• 當使用2進位制時， k=2 最小，位數 d 最大，時間複雜度 O(nd) 會變大，空間複雜度 O(n+k) 會變小。當用最大值作為基數時， k=maxV 最大， d=1 最小，此時時間複雜度 O(nd) 變小，但是空間複雜度 O(n+k) 會急劇增大，此時基數排序退化成了計數排序。

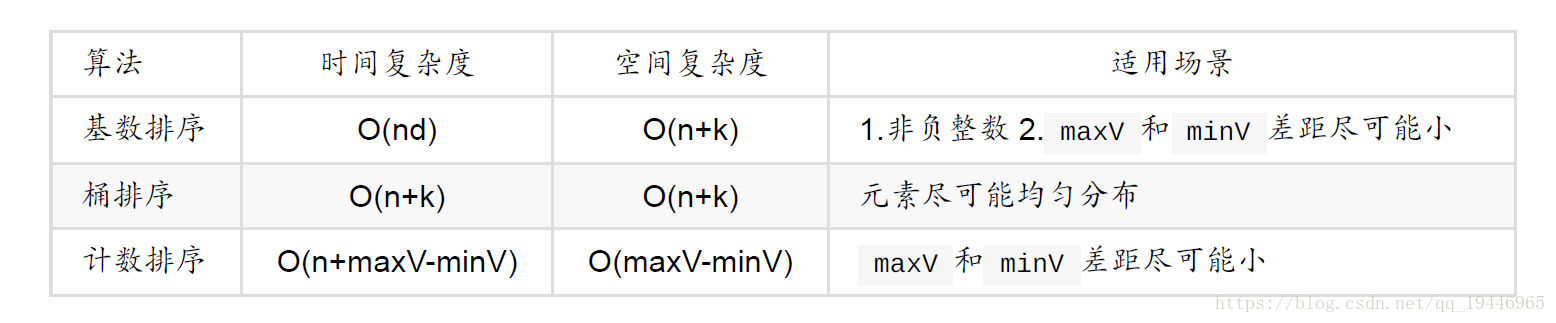
先比較時間複雜度和空間複雜度。

其中, d 表示位數， k 在基數排序中表示 k 進位制，在桶排序中表示桶的個數， maxV 和 minV 表示元
素最大值和最小值。

• 首先，基數排序和計數排序都可以看作是桶排序。
• 計數排序本質上是一種特殊的桶排序，當桶的個數取最大( maxV-minV+1 )的時候，就變成了計數排序。
• 基數排序也是一種桶排序。桶排序是按值區間劃分桶，基數排序是按數位來劃分；基數排序可以看做是多輪桶排序，每個數位上都進行一輪桶排序。
• 當用最大值作為基數時，基數排序就退化成了計數排序。
• 當使用2進位制時， k=2 最小，位數 d 最大，時間複雜度 O(nd) 會變大，空間複雜度 O(n+k) 會變小。當用最大值作為基數時， k=maxV 最大， d=1 最小，此時時間複雜度 O(nd) 變小，但是空間複雜度 O(n+k) 會急劇增大，此時基數排序退化成了計數排序。