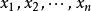矩陣的特徵值之積等於矩陣的行列式

矩陣的特徵值之和等於矩陣的跡

簡單的理解證明如下：

1、二次方程的韋達定理：

請思考：x^2+bx+c=0 這個方程的所有根的和等於多少、所有根的積等於多少

2、把二次方程推廣到 N 次：

對一個一元n次方程，它的根記作

那麼接下來可以類似地來思考：(x-x1)(x-x2)(x-x3)...(x-n_N)=0 這個方程的所有根的和對應於等式左邊展開後幾次項的係數，所有根的積對應等式展開後幾次項的係數。

說明：

已知一個一元五次方程：

根據高斯的代數原理：上式在複數範圍內必可分解成的形式；且x1, x2, x3, x4, x5是該多項式在複數範圍內的根。

3、考慮矩陣的特徵值問題

• 設A為n階方陣，考慮特徵多項式|A-λI|的n-1次項，有矩陣 A 的特徵值方程：det(A-λI)=0（行列式展開式在這裡不作說明，可以參考相關資料），我們可以發現，除了主對角元的乘積 (λ-a11)(λ-a22)...(λ-ann) 之外，其他展開項的次數都小於 n-1。因此 n-1 次項的係數就是 (λ-a11)(λ-a22)...(λ-ann) 中 λ^(n-1) 的係數，也就是-(a11+a22+...+ann)。
  特徵值是特徵多項式的根，由韋達定理（根與係數關係）知特徵值的和 = a11+a22+...+ann。

4、參考文獻：