[網路流] 二分圖匹配
阿新 • • 發佈:2019-01-10
二分圖匹配,本質上是最大流問題的一種特殊情況。
指派問題
有N臺計算機和K個任務,我們可以給每臺計算機分配一個任務,每臺計算機能夠處理的任務種類各不相同,請求出最多能夠處理的任務個數。
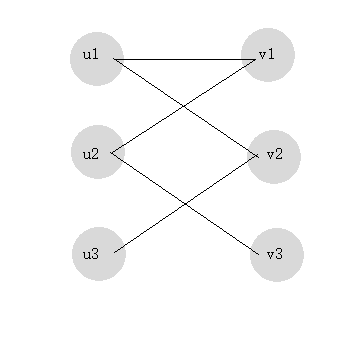
這個問題可以像下面這樣轉化為圖論模型來分析。我們可以像下面這樣來定義無向二分圖
U是代表計算機的頂點集合,V是代表任務的頂點集合,對於任意
u∈U和v∈V 計算機u能夠處理任務v⇒(u,v)∈E
而G中滿足兩兩不含公共端點的邊集合
圖論術語中,我們將這種兩兩不含公共端點的邊集合M稱為匹配,而元素最多的M則成為最大匹配。而元素最多的M則成為最大匹配。當最大匹配的匹配數滿足2|M| = V時,又稱為完美匹配。特別地,二分圖中的匹配又稱為二分圖匹配。向這道題一樣,二分圖匹配常常在指派問題的模型中出現,也常常在程式設計競賽中登場。
可以將二分圖最大匹配問題看成是最大流的一種特殊情況,對原圖做如下變形:
將原圖中的所有無相邊
e 改為有向邊,方向從U 到V ,容量為1 ,增加源點s 和匯點t ,從s 向所有的頂點u∈U 連一條容量為1的邊,從所有的頂點v∈V 向t 連一條容量為1的邊。
這樣變形得到的新圖中最大S-T流的流量就是原二分圖G中最大匹配的匹配數,而U-V之間流量為正的邊集合就是最大匹配。該演算法的複雜度為
//此處省略了部分建邊、尋找增廣路和求解最大流的程式碼
int N,K;
bool can[MAXN][MAXN];// can[i][j]:計算機i能夠處理任務j
void solve()
{
//0~N-1:計算機對應的頂點,