Javascript之資料結構與演算法的圖(Graph)實現
Javascript之資料結構與演算法的圖(Graph)實現
簡介
廣度優先搜尋演算法會從指定的第一個頂點開始遍歷圖,先訪問其所有的相鄰點,就像一次訪
問圖的一層。換句話說,就是先寬後深地訪問頂點。如圖:
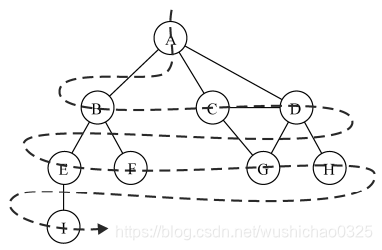
相關程式碼:
bfs(v,callback){ 深度優先搜尋將會從第一個指定的頂點開始遍歷圖,沿著路徑直到這條路徑最後一個頂
點被訪問了,接著原路回退並探索下一條路徑。換句話說,它是先深度後廣度地訪問頂點問所有節點。如圖:
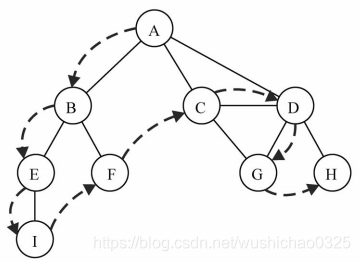
相關程式碼:
dfs(callback){
let color=this.initializeColor();
let vertices=items.get(this).vertices;
for(let i=0;i<vertices.length;i++){
if(color[vertices[i]]=='white'){
items.get(this).dfsVisit(items.get(this).adjList,items.get(this).dfsVisit,vertices[i],color,callback);
}
}
}
dfsVisit(adjList,dfsVisit,u,color,callback){
color[u]='grey';
if(callback){
callback(u);
}
let neighbors=adjList.get(u);
for(let i=0;i<neighbors.length;i++){
let w=neighbors[i];
if(color[w]=='white'){
dfsVisit(adjList,dfsVisit,w,color,callback);
}
}
color[u]='black';
}
廣度優先搜尋演算法實際應用-最短路徑(非權值)
問題背景:
給定一個圖G和源頂點v,找出對每個頂點u, u和v之間最短路徑的距離(以邊的數量計)。
解決辦法:
改良bfs演算法即BFS:
BFS(v){//-不加權最短路徑
let color=this.initializeColor();
let queue=new Queue();
let d=[];//存路徑
let pred=[];
queue.enqueue(v);
let vertices=items.get(this).vertices;
let adjList=items.get(this).adjList;
for(let i=0;i<vertices.length;i++){
d[vertices[i]]=0;
pred[vertices[i]]=null;
}
while(!queue.empty()){
let u=queue.dequeue();
let neighbors=adjList.get(u);
color[u]='grey';
for(let i=0;i<neighbors.length;i++){
let w=neighbors[i];
if(color[w]=='white'){
color[w]='grey';
d[w]=d[u]+1;
pred[w]=u;
queue.enqueue(w);
}
}
color[u]='black';
}
return {distances:d,predecessors:pred}
}
測試程式碼:
var graph = new Graph();
var myVertices = ['A','B','C','D','E','F','G','H','I']; //{7}
for (var i=0; i<myVertices.length; i++){ //{8}
graph.addVertex(myVertices[i]);
}
graph.addEdge('A', 'B'); //{9}
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('C', 'D');
graph.addEdge('C', 'G');
graph.addEdge('D', 'G');
graph.addEdge('D', 'H');
graph.addEdge('B', 'E');
graph.addEdge('B', 'F');
graph.addEdge('E', 'I');
var shortestPathA = graph.BFS(myVertices[0]);
console.log(shortestPathA);
//輸出結果:
distances: [A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2 , I: 3],
predecessors: [A: null, B: "A", C: "A", D: "A", E: "B", F: "B", G: "C", H: "D", I: "E"]
//顯示頂點到其他頂點的路徑
var fromVertex = myVertices[0];
for (var i=1; i<myVertices.length; i++){
var toVertex = myVertices[i],
path = new Stack();
for (var v=toVertex; v!== fromVertex;v=shortestPathA.predecessors[v]) {
path.push(v);
}
path.push(fromVertex);
var s = path.pop();
while (!path.isEmpty()){
s += ' - ' + path.pop();
}
console.log(s);
}
深度優先搜尋演算法實際應用-拓撲排序(有向無環圖)
編排一些任務或步驟的執行順序時,這稱為拓撲排序
例如:
當我們開始學習一門電腦科學課程,在學習某些知識之前得按順序完成一些知識儲備(你不可以在上演算法前先上演算法)。當我們在開發一個專案時,需要按順序執行一些步驟,例如,首先我們得從客戶那裡得到需求,接著開發客戶要求的東西,最後交付專案。
解決辦法:
改良版dfs即DFS:
DFS(){
let color=this.initializeColor();
let d=[];
let f=[];
let p=[];
items.get(this).time=0;
let vertices=items.get(this).vertices;
for(let i=0;i<vertices.length;i++){
f[vertices[i]]=0;
d[vertices[i]]=0;
p[vertices[i]]=null;
}
for(let i=0;i<vertices.length;i++){
if(color[vertices[i]]=='white'){
items.get(this).DFSVisit(items.get(this).time,items.get(this).adjList,items.get(this).DFSVisit,vertices[i],color,d,f,p);
}
}
return {
discovered:d,
finished:f,
predecessors:p
}
}
Dijkstra 演算法
Dijkstra演算法是一種計算從單個源到所有其他源的最短路徑的貪心演算法。
例如:
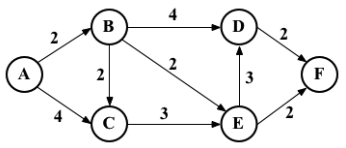
將圖上資訊轉化為鄰接矩陣:
graph.graph = [[0, 2, 4, 0, 0, 0],
[2, 0, 2, 4, 2, 0],
[4, 2, 0, 0, 3, 0],
[0, 4, 0, 0, 3, 2],
[0, 2, 3, 3, 0, 2],
[0, 0, 0, 2, 2, 0]];
相關程式碼:
//Dijkstra演算法
dijkstra(src){
let dist=[];
let INF=Number.MAX_SAFE_INTEGER;
let visited=[];
let length=this.graph.length;
for(let i=0;i<length;i++){//把所有的距離( dist)初始化為無限大( JavaScript最大的數INF = Number.MAX_SAFE_INTEGER),將visited[]初始化為false
dist[i]=INF;
visited[i]=false;
}
dist[src]=0;//把源頂點到自己的距離設為0
for(let i=0;i<length-1;i++){
let u=items.get(this).minDistance(dist,visited);//從尚未處理的頂點中選出距離最近的頂點
visited[u]=true;//把選出的頂點標為visited,以免重複計算
for(let v=0;v<length;v++){//查詢更短的路徑
if(!visited[v]&&this.graph[u][v]!=0&&dist[u]!=INF&&dist[u]+this.graph[u][v]<dist[v]){
dist[v]=dist[u]+this.graph[u][v];//更新最短路徑的值
}
}
}
return dist;
}
minDistance(dist,visited){
let INF=Number.MAX_SAFE_INTEGER;
let min=INF;
let minIndex=-1;
for(let v=0;v<dist.length;v++){
if(visited[v]==false&&dist[v]<=min){
min=dist[v];
minIndex=v;
}
}
return minIndex;
}
Floyd-Warshall 演算法
Floyd-Warshall演算法是一種計算圖中所有最短路徑的動態規劃演算法
//Floyd-Warshall演算法
floydWarshall(){
let INF=Number.MAX_SAFE_INTEGER;
let dist=[],
length=this.graph.length;
for(let i=0;i<length;i++){//首先,把dist陣列初始化為每個頂點之間的權值,因為i到j可能的最短距離就是這些頂點間的權值。
dist[i]=[];
for(let j=0;j<length;j++){
if(this.graph[i][j]==0&&i!=j){
dist[i][j]=INF;
}else{
dist[i][j]=this.graph[i][j];
}
}
}
for(let k=0;k<length;k++){//通過k,得到i途徑頂點0至k,到達j的最短路徑。
for(let i=0;i<length;i++){
for(let j=0;j<length;j++){
if(dist[i][k]+dist[k][j]<dist[i][j]){//通過k,得到i途徑頂點0至k,到達j的最短路徑。
dist[i][j]=dist[i][k]+dist[k][j];//如果是更短的路徑,則更新最短路徑的值
}
}
}
}
return dist;
}
最小生成樹(MST)-Prim演算法
實用背景:
你的公司有幾間辦公室,要以最低的成本實現辦公室電話線路相互連通,以節省資金;
在n個島嶼之間建造橋樑,想用最低的成本實現所有島嶼相互連通。
圖結構如下:
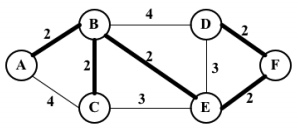
Prim演算法是一種求解加權無向連通圖的MST問題的貪心演算法。它能找出一個邊的子集,使得
其構成的樹包含圖中所有頂點,且邊的權值之和最小。
相關程式碼:
prim(){
let parent=[],
key=[],
visited=[],
length=this.graph.length,
INF=Number.MAX_SAFE_INTEGER;//代表無窮大即無路
for(let i=0;i<this.graph.length;i++){
for(let j=0;j<this.graph[i].length;j++){
if(this.graph[i][j]==0&&i!=j){
this.graph[i][j]=INF;
}
}
}
for(let i=0;i<length
相關推薦
Javascript之資料結構與演算法的圖(Graph)實現
Javascript之資料結構與演算法的圖(Graph)實現
簡介
廣度優先搜尋演算法實際應用-最短路徑(非權值)
深度優先搜尋演算法實際應用-拓撲排序(有向無環圖)
Dijkstra 演算法
Floyd-Warshall
Javascript之資料結構與演算法的自平衡二叉搜尋樹(AVL)實現
Javascript之資料結構與演算法的自平衡二叉搜尋樹(AVL)實現
簡介
程式碼實現
簡介
AVL樹是一種自平衡樹。新增或移除節點時, AVL樹會嘗試自平衡。任意一個節點(不論深 度)的左子樹和右子樹高度最多相差1
javascript資料結構與演算法筆記(一):棧
javascript資料結構與演算法筆記(一):棧
一:簡介
二:ES6版Stack類(陣列)
三:ES版Stack類私有屬性的封裝
1.偽私有屬性封裝
2.真私有屬性封裝
javascript資料結構與演算法筆記(六):雙向連結串列
javascript資料結構與演算法筆記(六):雙向連結串列
一:簡介
二:ES6版DoublyLinkedList類
一:簡介
雙向連結串列和普通連結串列的區別在於,在連結串列中,一個節點只有鏈向下一個節點的連結,而
javascript資料結構與演算法筆記(五):連結串列
javascript資料結構與演算法筆記(五):連結串列
一:簡介
二:ES6版LinkedList類
一:簡介
連結串列儲存有序的元素集合,但不同於陣列,連結串列中的元素在記憶體中並不是連續放置的。每個 元素由一個儲
javascript資料結構與演算法筆記(四):迴圈佇列
javascript資料結構與演算法筆記(四):迴圈佇列
一:簡介
二:ES6版Queue類
一:簡介
迴圈佇列是指佇列頭元素的移除會追加到佇列的尾部。我們此次拿一個例子來實現迴圈佇列,例子名就是模擬民間遊戲擊鼓傳花即
javascript資料結構與演算法筆記(三):優先佇列
javascript資料結構與演算法筆記(三):優先佇列
一:簡介
二:ES6版PriorityQueue類
一:簡介
優先佇列是元素的新增和移除是基於優先順序的。一個現實的例子就是機場登機的順序。頭等艙和商務艙乘客的
javascript資料結構與演算法筆記(二):普通佇列
javascript資料結構與演算法筆記(二):普通佇列
一:簡介
二:ES6版Queue類
一:簡介
佇列是遵循FIFO( First In First Out, 先進先出,也稱為先來先服務)原則的一組有序的項。 佇
Javascript之資料結構與演算法的二叉樹和二叉搜尋樹實現
Javascript之資料結構與演算法的二叉樹和二叉搜尋樹實現
簡介
程式碼實現
簡介
二叉樹中的節點最多隻能有兩個子節點:一個是左側子節點,另一個是右側子節點。 二叉搜尋樹( BST)是二叉樹的一種,但是它只允許你在
Javascript之資料結構與演算法的HashMap實現
Javascript之資料結構與演算法的HashMap實現
1.自實現HashMap
1.自實現HashMap
let LinkedList=require("./LinkedList")
let loseloseHashCo
Javascript之資料結構與演算法的Dictionary實現
Javascript之資料結構與演算法的Dictionary實現
1.自實現Dictionary
2.Es6中Map對比
3.Map總結
4.Es6中WeakMap類和WeakSet類
1.自實現Dicti
Javascript之資料結構與演算法的Set實現
Javascript之資料結構與演算法的Set實現
1.ES6中的Set
2.自實現Set
1.ES6中的Set
請參考官網API:http://caibaojian.com/es6/set-map.html
2.
資料結構與演算法入門(1)
一、資料結構 資料之間相互存在的一種或多種特定的關係的元素的集合。 邏輯結構 資料物件中資料元素之間的相互關係 1.集合結構 在資料結構中,如果不考慮資料元素之間的關係,這種結構稱為集合結構。 各個元素是平等的,共同屬性是屬於同一個集合 2.線性結構 線性結構中的資料元素之間
資料結構與演算法筆記(二)複雜度分析
2. 複雜度分析
2.1 什麼是複雜度分析
資料結構和演算法的本質:快和省,如何讓程式碼執行得更快、更省儲存空間。
演算法複雜度分為時間複雜度和空間複雜度,從執行時間和佔用空間兩個維度來評估資料結構和演算法的效能。
複雜度描述的是演算法執行時間(或佔用空間)與資料規模的增長關
資料結構與演算法筆記(三)陣列
3.陣列
陣列(Array)是一種線性表資料結構。它是一組連續的記憶體空間,來儲存一組具有相同型別的資料。
3.1 特性
線性表 資料排成像一條線的結構,如陣列、連結串列、佇列、棧等。 與之相對立的是非線性,如二叉樹、堆、圖等,其資料之間並不是簡單的前後關係。
資料結構與演算法筆記(三)反轉部分連結串列
反轉部分連結串列
上次我們搞定了反轉單向連結串列和雙向連結串列的問題,但實際過程中我們可能只要反轉部分連結串列,在這種情況下我們需要對上次寫出的類增加一個叫做reverse_part_linklist的函式,傳入引數為兩個整數from和to,將from到to之間的節點進行反轉
資料結構與演算法複習(15)—— 博弈論
一批文章:
http://hi.baidu.com/liveroom/blog/category/%B2%A9%DE%C4%C2%DB
http://blog.csdn.net/logic_nut/archive/2009/10/21/4706649.aspx
http://blog.csdn.net/lo
資料結構與演算法複習(10)—— 字尾陣列與字串問題
放此待查。
RMQ 問題
http://www.notonlysuccess.com/?p=356
利用字尾陣列求解一個字串中最長重複子串問題
http://cylixstar.blogbus.com/logs/28350301.html
http://imlazy.ycool.com/post.20118
資料結構與演算法複習(3)—— 線段樹
http://www.cppblog.com/MemoryGarden/archive/2009/04/11/79565.aspx
http://www.notonlysuccess.com/?p=59
http://edu.codepub.com/2009/1125/18163.php
POJ 2104,
資料結構與演算法總結(六)詞典
詞典結構:dict允許多個詞條擁有相同的關鍵碼。詞條為關鍵碼與值的合成結構。
對映結構:map要求不同詞條的關鍵碼互不相同。
例如跳轉表:一種高效的詞典結構,基於列表構造,時間複雜度為O(logn)。就是橫層連結串列代表關鍵碼,縱向列表代表值。一個關鍵碼代表多個一樣的值。
詞典dict操
