旋轉卡殼詳解

轉載來源：https://blog.csdn.net/qq_34921856/article/details/80690822 （應博主要求 我是博主粉絲）
另一篇部落格

問題描述

基本問題為O(n)求凸n角形的對踵點,而由該問題可以引申出許多的難題，他們包括:

• 計算距離

  • 凸多邊形直徑
  • 凸多邊形寬
  • 凸多邊形間最大距離
  • 凸多邊形間最小距離

• 外接矩形

  • 最小面積外接矩形
  • 最小周長外接矩形

問題求解

計算距離

• 凸多邊形直徑
  我們將一個多邊形上任意兩點間的距離的最大值定義為多邊形的直徑。 確定這個直徑的點對數可能多於一對。 事實上， 對於擁有 n 個頂點的多邊形， 就可能有 n 對“直徑點對”存在。
  
  
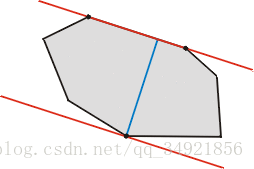
  一個多邊形直徑的簡單例子如左圖所示。 直徑點對在圖中顯示為被平行線穿過的黑點 （紅色的一對平行線）. 直徑用淺藍色高亮顯示。
  顯然， 確定一個凸多邊形 P 直徑的點對不可能在多邊形 P 內部。 故搜尋應該在邊界上進行。 事實上， 由於直徑是由多邊形的平行切線的最遠距離決定的， 所以我們只需要查詢對踵點。 Shamos (1978) 提供了一個 O(n) 時間複雜度計算n點凸包對踵點對的演算法。直徑通過遍歷頂點列表， 得到最大距離即可。

演算法描述
1. 計算多邊形$y$方向的端點，我們稱之為$ymin$和$ymax$
2. 通過$ymin$和$ymax$構造兩條水平切線。由於他們已經是一對對踵點，計算他們之間的距離並維護一個當前的最大值。
3. 同時旋轉兩條線直到其中一條與多邊形的一邊重合。
4. 一個新的對踵點對此時產生。計算新的距離，並和當前的最大值比較，大於當前最大值則更新。
5. 重複步驟3和步驟4的過程直到再次產生對踵點對。
6. 輸出確定最大直徑的對踵點對。

程式碼:

void solve2(int num)
{
    int ymax=-1e5,ymin=1e5;
    int ymaxidx,yminidx;
    for(int i=1;i<=num;i++)
    {
        if(ch[i].y>ymax)
        {
            ymax=ch[i].y;
            ymaxidx=i;
        }
        if(ch[i].y<ymin)
        {
            ymin=ch[i].y;
            yminidx=i;
        }
    }
    int
 
 ans=dis2(ch[ymaxidx]-ch[yminidx]);
    ch[num+1]=ch[1];
    for(int t=1;t<=num;t++,yminidx=yminidx%num+1)
    {
        while(xmult(ch[yminidx+1],ch[ymaxidx+1],ch[yminidx])>xmult(ch[yminidx+1],ch[ymaxidx],ch[yminidx]))ymaxidx=ymaxidx%num+1;
        ans=max(ans,dis2(ch[ymaxidx]-ch[yminidx]));
        ans=max(ans,dis2(ch[ymaxidx]-ch[yminidx+1]));
    }
    printf("%d\n",ans);
}

• 凸多邊形寬度
  凸多邊形的寬度定義為平行切線間的最小距離。這個定義從寬度這個詞已經略有體現。雖然凸多邊形的切線有不同的方向，並且每個方向的寬度通常是不同的。但幸運的是，不是所有的方向都要計算。
  我們假設存在一個線段[a,b],以及兩條通過a和b的平行線，通過繞著這兩個點旋轉這兩條線，使他們的距離遞增或遞減，特別的，總存在一個特定的方向使得兩條線段的距離通過旋轉變小。
  這個簡單的結論可以用到計算寬度中:不是所有的方向都要考慮，假設給定一個凸多邊形後，同時還有兩條平行切線。如果他們都未與邊重合，那麼我們總能通過旋轉來減少他們的距離，因此，兩條平行切線只有在其中至少一條與邊重合的情況下才能確定多邊形的寬度。
  這就意味著”對踵點 點-邊”以及“邊-邊”對需要在計算寬度過程中被考慮。
  
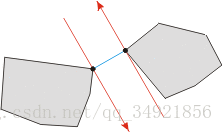
  一個凸多邊形寬度的示意圖。 直徑對如圖由平行切線（紅線）穿過的黑點所示。 直徑如高亮的淡藍色線所示。

一個與計算直徑問題非常相似的演算法可以通過遍歷多邊形對踵點對列表得到， 確定頂點-邊以及邊-邊對來計算寬度。 選擇過程如下:
1. 計算多邊形$y$方向的端點，我們稱之為$ymin$和$ymax$
2. 通過$ymin$和$ymax$構造兩條水平切線，如果一條(或者兩條)與邊重合，那麼一個”對踵點 點-邊”或者”邊-邊”對已經確定，此時計算兩線間的距離，並且存為當前最小距離。
3. 同時旋轉兩條線直到其中一條線與多邊形的一邊重合。
4. 一個新的對踵點對(“點-邊或者邊-邊”)此時產生。計算新的距離，並和當前的最小值比較，小於當前最小值則更新。
5. 重複3和4的過程知道再次達到最初的平行線的位置。
6. 將獲得的最小值的對作為確定寬度的對輸出。

程式碼與上面類似，略。

• 凸多邊形間的最大距離

給定兩個凸多邊形P和Q，目標是需要找到點對(p,q)(p屬於P,q屬於Q)使得他們之間的距離最大。
很直觀的，這些點不屬於他們的內部。這個條件事實上與直徑問題非常類似。

兩凸多邊形P和Q間最大距離由多邊形對踵點對確定。
雖然說法一樣，但是這個定義與給定凸多邊形的對踵點對的不同。
與凸多邊形間的對踵點對本質上的區別在於切線是有向且反向的，下圖展示了一個例子:

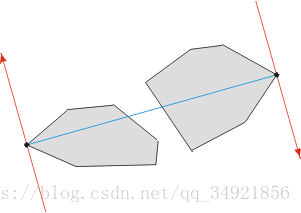
注:雖然意思相同，但博主的程式碼所描述的切線方向與本圖相反，即所代表的面積都為切線的左邊方向而不是圖中的右邊方向。
上述結論暗示不單純只是頂點對需要檢測，而僅僅是特定的頂點對需要被考慮，實際上他們只間測一個基於旋轉卡殼模式的演算法確立的平行切線。
考慮如下的演算法，演算法的輸入是兩個分別有m和n個逆時針給定頂點的凸多邊形P和Q。
1. 計算P上y座標最小的頂點(稱為yminP)和Q上y座標值最大的頂點(稱為ymaxQ)。
2. 為多邊形在yminP和ymaxQ處構造兩條切線LP和LQ使得他們對應的多邊形都位於他們的左側，此時LP和LQ擁有不同的方向，並且yminP和ymaxQ成為多邊形間的一個對踵點對。
3. 計算距離(yminP和ymaxQ)並且將其維護一個最大值。
4. 逆時針同時旋轉平行線直到其中一個與其所在的多邊形的邊重合。
5. 一個新的對踵點對產生了，計算新距離，與當前最大值比較，如果大於當前最大值則更新。如果兩條線同時與邊發生重合，此時總共四個對踵點對(點-點)(先前頂點和新頂點的組合)需要考慮在內。
6. 重複執行步驟4和步驟5，直到新的點對為(yminP,ymaxQ).
7. 輸出最大距離。

• 凸多邊形間的最小距離

給定兩個非連線(比如不相交)的凸多邊形P和Q，目標是找到擁有最小距離的點對(p,q)(p屬於P且q屬於Q)。
事實上，多邊形非連線十分重要，因為我們所說的多邊形包含其內部，如果多邊形相交，那麼最小距離就變得沒有意義了。然而，對於這個問題的另一版本，凸多邊形頂點間最小距離對於相交和非相交的情況都有解存在。

回到我們的主問題：直觀的，確定最小距離的點不可能包含在多邊形內部。與最大距離問題相似，我們有如下結論:

兩個凸多邊形P和Q之間的最小距離由多邊形間的對踵點對確立。存在凸多邊形三種多邊形間的對踵點對， 因此就有三種可能存在的最小距離模式：
1. “頂點-頂點”的情況
2. “頂點-邊”的情況
3. “邊-邊”的情況

換句話說， 確定最小距離的點對不一定必須是頂點。 下面的三個圖例表明了以上結論：

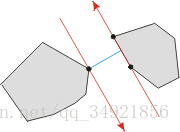
注:雖然意思相同，但博主的程式碼所描述的切線方向與本圖相反，即所代表的面積都為切線的左邊方向而不是圖中的右邊方向。
給定結果， 一個基於旋轉卡殼的演算法自然而然的產生了:
考慮如下的演算法， 演算法的輸入是兩個分別有 m 和 n 個逆時針給定頂點的凸多邊形 P 和 Q。
1. 計算 P 上 y 座標值最小的頂點（稱為 yminP ） 和 Q 上 y 座標值最大的頂點（稱為 ymaxQ）。
2. 為多邊形在 yminP 和 ymaxQ 處構造兩條切線 LP 和 LQ 使得他們對應的多邊形位於他們的左側。 此時 LP和 LQ 擁有不同的方向， 並且 yminP 和 ymaxQ 成為了多邊形間的一個對踵點對。
3. 計算距離(yminP,ymaxQ) 並且將其維護為當前最小值。
4. 逆時針同時旋轉平行線直到其中一個與其所在的多邊形的邊重合。
5. 如果只有一條線與邊重合， 那麼只需要計算“頂點-邊”對踵點對和“頂點-頂點”對踵點對距離(點到線段的距離)。 都將他們與當前最小值比較， 如果小於當前最小值則進行替換更新。 如果兩條切線都與邊重合， 則計算線段到線段的距離。 所有的這些距離都與當前最小值進行比較， 若小於當前最小值則更新替換。
6. 重複執行步驟4和步驟5， 直到新的點對為(yminP,ymaxQ)。
7. 輸出最大距離。

程式碼:

double solve(Point *a,int anum,Point *b,int bnum)
{
    int i;
    double tmp,res=1e10;
    a[anum+1]=a[1],b[bnum+1]=b[1];
    int p,q;
    double ymin=1e5,ymax=-1e5;
    for(i=1;i<=anum;i++)
    {
        if(a[i].y<ymin)
        {
            ymin=a[i].y;
            p=i;
        }
    }
    for(i=1;i<=bnum;i++)
    {
        if(b[i].y>ymax)
        {
            ymax=b[i].y;
            q=i;
        }
    }

    for(i=1;i<=anum;i++)
    {
        while(sgn((tmp=((a[p+1]-a[p])^(b[q+1]-a[p]))-((a[p+1]-a[p])^(b[q]-a[p]))))>0)
            q=q%bnum+1;
        if(sgn(tmp)<0)res=min(res,disptoseg(b[q],a[p],a[p+1]));
        else res=min(res,dissegtoseg(a[p],a[p+1],b[q],b[q+1]));
        p=p%anum+1;
        //cout<<res<<endl;
    }
    return res;
}

注:在計算時並不知道這兩個凸多邊形的相對位置，因此可能計算出來的值比最小值大，故在用的時候需要這樣:

double tmp=solve(ch1,p1num,ch2,p2num);
printf("%.5f\n",min(tmp,solve(ch2,p2num,ch1,p1num)));

最小距離及最大距離的問題表明了旋轉卡殼模型可以用在不同的條件下(與先前的直徑和寬度問題比較)。這個模型可以用在兩個凸多邊形的問題上。

“最小盒子”問題(最小面積外接矩陣)通過同一多邊形的兩個正交切線集合展示了另一種條件下的旋轉卡殼的應用。

外接矩形

• 凸多邊形最小面積外接矩陣

給定一個凸多邊形 P ， 面積最小的能裝下 P （就外圍而言）的矩形是怎樣的呢？ 從技術上說， 給定一個方向， 能計算出 P 的端點並且構由此造出外接矩形。 但是我們需要測試每個情形來獲得每個矩形來計算最小面積嗎？ 謝天謝地， 我們不必那麼幹。

對於多邊形 P 的一個外接矩形存在一條邊與原多邊形的邊共線。

上述結論有力地限制了矩形的可能範圍。 我們不僅不必去檢測所有可能的方向， 而且只需要檢測與多邊形邊數相等數量的矩形。

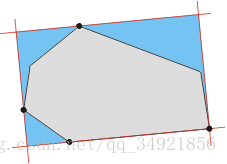
圖示上述結論： 四條切線（紅色）， 其中一條與多邊形一條邊重合， 確定了外接矩形（藍色）。
一個簡單的演算法是依次將每條邊作為與矩形重合的邊進行計算。 但是這種構造矩形的方法涉及到計算多邊形每條邊端點， 一個花費 O(n) 時間（因為有 n 條邊）的計算。 整個演算法將有二次時間複雜度。

一個更高效的演算法已經發現。 利用旋轉卡殼， 我們可以在常數時間內實時更新， 而不是重新計算端點。
實際上， 考慮一個凸多邊形， 擁有兩對和 x 和 y 方向上四個端點相切的切線。 四條線已經確定了一個多邊形的外接矩形。 但是除非多邊形有一條水平的或是垂直的邊， 這個矩形的面積就不能算入最小面積中。
然而， 可以通過旋轉線直到條件滿足。 這個過程是下屬演算法的核心。 假設按照順時針順序輸入一個凸多邊形的n 個頂點。

1. 計算全部四個多邊形的端點， 稱之為 xminP， xmaxP， yminP， ymaxP。
2. 通過四個點構造 P 的四條切線。 他們確定了兩個“卡殼”集合。
3. 如果一條（或兩條）線與一條邊重合， 那麼計算由四條線決定的矩形的面積， 並且儲存為當前最小值。 否則將當前最小值定義為無窮大。
4. 順時針旋轉線直到其中一條和多邊形的一條邊重合。
5. 計算新矩形的面積， 並且和當前最小值比較。 如果小於當前最小值則更新， 並儲存確定最小值的矩形資訊。
6. 重複步驟4和步驟5， 直到線旋轉過的角度大於90度。
7. 輸出外接矩形的最小面積。

程式碼:

double solve(int num)
{
    int r=2,q=2,p;
    double res=1e10;
    ch[num+1]=ch[1];
    for(int i=1;i<=num;i++)
    {
        while(sgn(xmult(ch[i+1],ch[r+1],ch[i])-xmult(ch[i+1],ch[r],ch[i]))>0)r=r%num+1;
        while(sgn(dot(ch[i+1],ch[q+1],ch[i])-dot(ch[i+1],ch[q],ch[i]))>0)q=q%num+1;
        if(i==1)p=q;
        while(sgn(dot(ch[i+1],ch[p+1],ch[i])-dot(ch[i+1],ch[p],ch[i]))<=0)p=p%num+1;
        double a=xmult(ch[i+1],ch[r],ch[i]);
        double b=dot(ch[i+1],ch[q],ch[i])-dot(ch[i+1],ch[p],ch[i]);
        double c=dot(ch[i+1],ch[i+1],ch[i]);
        res=min(res,a*b/c);
    }
    return res;
}

• 凸多邊形最小周長外接矩形
  這個問題和最小面積外接矩形相似。 我們的目標是找到一個最小盒子（就周長而言）外接多邊形 P 。

有趣的是通常情況下最小面積的和最小周長的外接矩形是重合的。 有人不禁想問這是不是總成立的。 下面的例子回答了這個問題： 多邊形（灰色的）及其最小面積外接矩形（左邊的）和最小周長外接矩形（右邊的）。

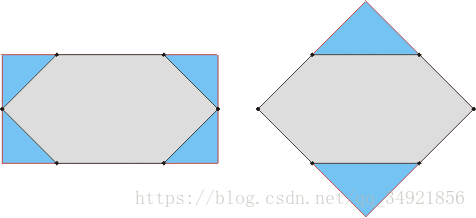
現在， 給定一個方向， 我們可以算出 P 的端點， 以此來確定一個外接矩形。 但是， 就如同面積問題中一樣， 由於有下面的結論， 我們不必檢測每個狀態來獲得擁有最小周長的矩形：

凸多邊形 P 的最小周長外接矩形存在一條邊和多邊形的一條邊重合。

這個結論通過列舉多邊形的一條重合邊有力地限制了矩形的可能範圍.

圖示上述結論： 四條切線（紅色）， 其中一條與多邊形邊重合， 確定了外接矩形（藍色）。
因為與其面積問題相當， 這個問題可以通過一個基於旋轉卡殼的相似的演算法來解決。
下屬演算法的輸入是順時針順序給定的一個凸多邊形的 n 個頂點。
1. 計算全部四個多邊形的端點， 稱之為 xminP， xmaxP， yminP， ymaxP。
2. 通過四個點構造 P 的四條切線。 他們確定了兩個“卡殼”集合。
3. 如果一條（或兩條）線與一條邊重合， 那麼計算由四條線決定的矩形的面積， 並且儲存為當前最小值。 否則將當前最小值定義為無窮大。
4. 順時針旋轉線直到其中一條和多邊形的一條邊重合。
5. 計算新矩形的周長， 並且和當前最小值比較。 如果小於當前最小值則更新， 並儲存確定最小值的矩形資訊。
6. 重複步驟4和步驟5， 直到線旋轉過的角度大於90度。
7. 輸出外接矩形的最小周長。
因為兩對的“卡殼”確定了一個外接矩形， 這個演算法考慮到了所有可能算出最小周長的矩形。 進一步， 除了初始值外， 演算法的主迴圈只需要執行頂點總數多次。 因此演算法是線性時間複雜度的。
程式碼和上面類似，故略。