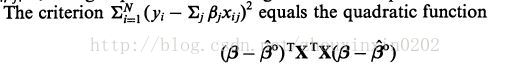前言：本文包括以下幾個方面，1. 介紹Lasso，從最初提出Lasso的論文出發，注重動機；

2. L1和L2範數的比較，注重L1的稀疏性及魯棒性；

3. 從誤差建模的角度理解L1範數

1. lasso

最早提出Lasso的文章，文獻[1]，已被引用n多次。

注：對於不曉得怎麼翻譯的英文，直接搬來。

1) 文獻[1]的動機：

在監督學習中，ordinary least squares(OLS) estimates 最小化所有資料的平方殘差（即只是讓經驗誤差最小化），存在2個問題：

1是預測誤差（prediction accuracy）：OLS estimates總是偏差小，方差大；

2是可解釋性（interpretation）：我們希望選出一些有代表性的子集就ok了。

【Lasso還有個缺點，ref8：當p>>n時，（如 醫學樣本，基因和樣本數目)，Lasso卻最多隻能選擇n個特徵】

為了解決上面2個問題，2種技術應運而生：

1是subset selection：其可解釋性強，但預測精度可能會很差；

2是嶺迴歸(ridge regression)：其比較穩定（畢竟是添加了正則化項，把經驗風險升級為結構風險），

                                                但可解釋性差（只是讓所有coefficients都很小，沒讓任何coefficients等於0）。

看來這2種技術對於2大問題總是顧此失彼，Lasso就被提出啦！其英文全稱是'least absolute shrinkage and selection operator'

lasso的目的是：shrink  some coefficients and sets others to 0，

                           保留subset selection可解釋性強的優點 和 ridge regression穩定性強的優點。

2）為什麼Lasso相比ridge regression稀疏？

直觀的理解[1]

(plus a constant).

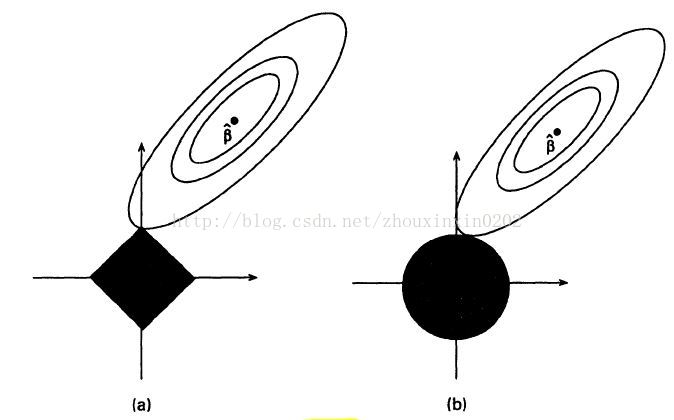
(a)圖：橢圓形是函式的影象，lasso的約束影象是菱形。

最優解是第一次橢圓線觸碰到菱形的點。最優解容易出現在角落，如圖所示，觸碰點座標是(0,c)，等同於一個coefficient=0;

(b)圖：嶺迴歸的約束影象是圓形。

因為圓形沒有角落，所以橢圓線與圓形的第一次觸碰很難是在座標為(0,c)的點，也就不存在稀疏了。

2.  L1,L2範數誤差的增長速度（ref2,ref3）

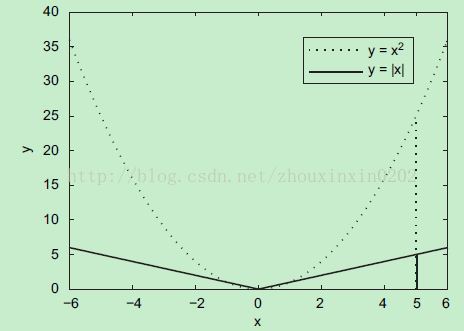
                 圖1

L1範數誤差的線性增長速度使其對大噪音不敏感，從而對不良作用形成一種抑制作用。

而L2範數誤差的二次增長速度 顯著放大了 大噪聲 負面作用。

3. 從誤差建模的角度理解

1）孟德宇老師從誤差建模的角度分析L1如何比L2魯棒。(ref3)

1：看圖1，由於L1範數的線性增長速度使其對大噪音不敏感，從而對其不良影響起到一種隱式抑制，因此相對魯棒。

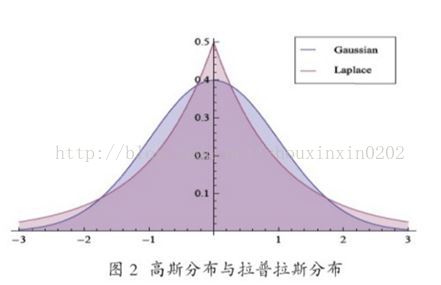
2：從貝葉斯的角度，看圖2，L1範數誤差對應的拉普拉斯分佈比L2範數誤差對應的高斯分佈具有更為顯著的“厚尾”狀態，從而其更適合對大幅度噪音的似然描述，

從而導致對大噪音或異常點資料更加穩健的計算效果。

2）1是從誤差建模的角度，涉及這麼個問題：從貝葉斯角度，為什麼L1對應拉普拉斯，L2對應高斯分佈呢？

這個問題我糾結了好久，因為RCC論文涉及此分析。終於從知乎https://www.zhihu.com/question/23536142上找到解析：

1是參考博文 ref 6:  （ 文章含具體推導，分為L1、L2、Elastic Net（L2及L1+L2） ）

    拋給大家一個結論：從貝葉斯的角度來看，正則化等價於對模型引數引入 先驗分佈 。

    對於迴歸問題，對w引入先驗分佈(高斯分佈/拉普拉斯分佈) -> 對樣本空間 關於w 求貝葉斯最大後驗估計（MAP） -> 得到了關於w的嶺迴歸/LASSO 

    因此， 對引數引入 高斯先驗/拉普拉斯先驗 等價於 L2正則化/L1正則化

2是參考論文 ref 7: ( ref6的進階 )

     除了高斯先驗、拉普拉斯先驗，還講了其他先驗。   

4. ref4

L0範數很難優化求解（NP難問題），L1範數是L0範數的最優凸近似，比L0範數容易優化求解。

5. ref5 一篇極好的博文，全面分析了各種範數（L1，L2，核範數，魯棒PCA）

參考：

[1]《Regression shrinkage and selection via the lasso》Robert Tibshirani

[2] 《Improve robustness of sparse PCA by L1-norm maximization》 Meng Deyu et.al

[3] 《誤差建模原理》孟德宇  人工智慧通訊

[4] 《convex optimization》S.Boyd  (書)

[5] http://blog.csdn.net/lj695242104/article/details/38801025   (csdn部落格，總結的很好)