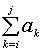演算法設計與分析--求最大子段和問題(蠻力法、分治法、動態規劃法) C++實現
阿新 • • 發佈:2019-01-11
演算法設計與分析--求最大子段和問題
問題描述:
給定由n個整陣列成的序列(a1,a2, …,an),求該序列形如
的子段和的最大值,當所有整數均為負整數時,其最大子段和為0。
利用蠻力法求解:
int maxSum(int a[],int n) { int maxSum = 0; int sum = 0; for(int i = 0; i < n; i++) //從第一個數開始算起 { for(int j = i + 1; j < n; j++)//從i的第二個數開始算起 { sum = a[i]; a[i] += a[j]; if(a[i] > sum) { sum = a[i]; //每一趟的最大值 } } if(sum > maxSum) { maxSum = sum; } } return maxSum; }
利用分治法求解:
int maxSum(int a[],int left, int right) { int sum = 0; if(left == right) //如果序列長度為1,直接求解 { if(a[left] > 0) sum = a[left]; else sum = 0; } else { int center = (left + right) / 2; //劃分 int leftsum = maxSum(a,left,center); //對應情況1,遞迴求解 int rightsum = maxSum(a, center + 1, right);//對應情況2, 遞迴求解 int s1 = 0; int lefts = 0; for(int i = center; i >= left; i--) //求解s1 { lefts += a[i]; if(lefts > s1) s1 = lefts; //左邊最大值放在s1 } int s2 = 0; int rights = 0; for(int j = center + 1; j <= right; j++)//求解s2 { rights += a[j]; if(rights > s2) s2 =rights; } sum = s1 + s2; //計算第3鍾情況的最大子段和 if(sum < leftsum) sum = leftsum; //合併,在sum、leftsum、rightsum中取最大值 if(sum < rightsum) sum = rightsum; } return sum; }
利用動態規劃法求解:
int DY_Sum(int a[],int n) { int sum = 0; int *b = (int *) malloc(n * sizeof(int)); //動態為陣列分配空間 b[0] = a[0]; for(int i = 1; i < n; i++) { if(b[i-1] > 0) b[i] = b[i - 1] + a[i]; else b[i] = a[i]; } for(int j = 0; j < n; j++) { if(b[j] > sum) sum = b[j]; } delete []b; //釋放記憶體 return sum; }
完整測試程式:
#include<iostream>
#include<time.h>
#include<Windows.h>
using namespace std;
#define MAX 10000
int BF_Sum(int a[],int n)
{
int max=0;
int sum=0;
int i,j;
for (i=0;i<n-1;i++)
{
sum=a[i];
for(j=i+1;j<n;j++)
{
if(sum>=max)
{
max=sum;
}
sum+=a[j];
}
}
return max;
}
int maxSum1(int a[],int left, int right)
{
int sum = 0;
if(left == right) //如果序列長度為1,直接求解
{
if(a[left] > 0) sum = a[left];
else sum = 0;
}
else
{
int center = (left + right) / 2; //劃分
int leftsum = maxSum1(a,left,center); //對應情況1,遞迴求解
int rightsum = maxSum1(a, center + 1, right);//對應情況2, 遞迴求解
int s1 = 0;
int lefts = 0;
for(int i = center; i >= left; i--) //求解s1
{
lefts += a[i];
if(lefts > s1) s1 = lefts; //左邊最大值放在s1
}
int s2 = 0;
int rights = 0;
for(int j = center + 1; j <= right; j++)//求解s2
{
rights += a[j];
if(rights > s2) s2 =rights;
}
sum = s1 + s2; //計算第3鍾情況的最大子段和
if(sum < leftsum) sum = leftsum; //合併,在sum、leftsum、rightsum中取最大值
if(sum < rightsum) sum = rightsum;
}
return sum;
}
int DY_Sum(int a[],int n)
{
int sum = 0;
int *b = (int *) malloc(n * sizeof(int)); //動態為陣列分配空間
b[0] = a[0];
for(int i = 1; i < n; i++)
{
if(b[i-1] > 0)
b[i] = b[i - 1] + a[i];
else
b[i] = a[i];
}
for(int j = 0; j < n; j++)
{
if(b[j] > sum)
sum = b[j];
}
delete []b; //釋放記憶體
return sum;
}
int main()
{
int num[MAX];
int i;
const int n = 40;
LARGE_INTEGER begin,end,frequency;
QueryPerformanceFrequency(&frequency);
//生成隨機序列
cout<<"生成隨機序列:";
srand(time(0));
for(int i = 0; i < n; i++)
{
if(rand() % 2 == 0)
num[i] = rand();
else
num[i] = (-1) * rand();
if(n < 100)
cout<<num[i]<<" ";
}
cout<<endl;
//蠻力法//
cout<<"\n蠻力法:"<<endl;
cout<"最大欄位和:";
QueryPerformanceCounter(&begin);
cout<<BF_Sum(num,n)<<endl;
QueryPerformanceCounter(&end);
cout<<"時間:"
<<(double)(end.QuadPart - begin.QuadPart) / frequency.QuadPart
<<"s"<<endl;
cout<<"\n分治法:"<<endl;
cout<"最大欄位和:";
QueryPerformanceCounter(&begin);
cout<<maxSum1(num,0,n)<<endl;
QueryPerformanceCounter(&end);
cout<<"時間:"
<<(double)(end.QuadPart - begin.QuadPart) / frequency.QuadPart
<<"s"<<endl;
cout<<"\n動態規劃法:"<<endl;
cout<"最大欄位和:";
QueryPerformanceCounter(&begin);
cout<<DY_Sum(num,n)<<endl;
QueryPerformanceCounter(&end);
cout<<"時間:"
<<(double)(end.QuadPart - begin.QuadPart) / frequency.QuadPart
<<"s"<<endl;
system("pause");
return 0;
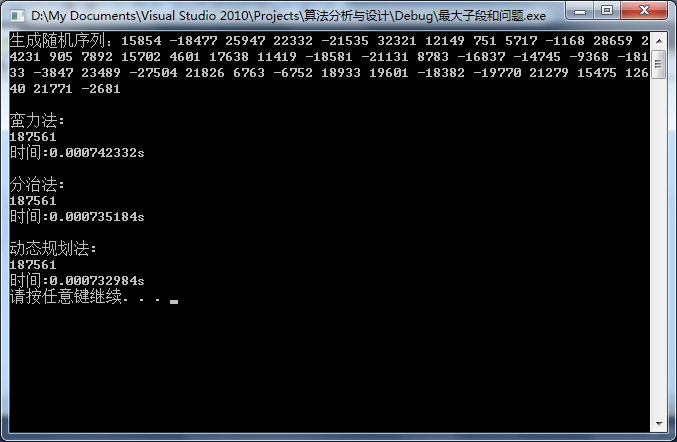
}測試結果: