九章演算法4:動態規劃I
遞迴和動態規劃
從Triangle這個問題說起:
題目:
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
Example:
Given the following triangle:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
三種解法
遇到這道題,老師說開始先給出暴力解法之後進行優化是可以的,不一定一開始就給出最優解,想出來一個暴力解法覺得傻就不說話。。。
- DFS:Traverse
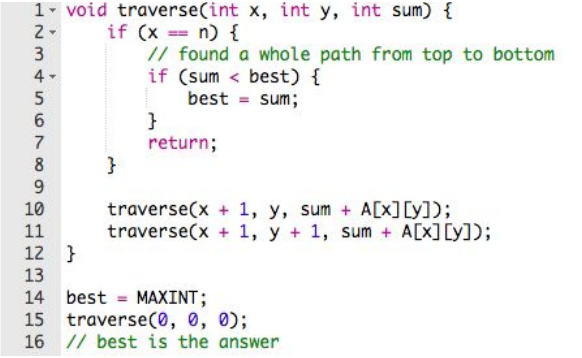
其中時間複雜度為
- DFS:Divide and Conquer

時間複雜度依然為
-DFS:Divide and Conquer 加 memorization
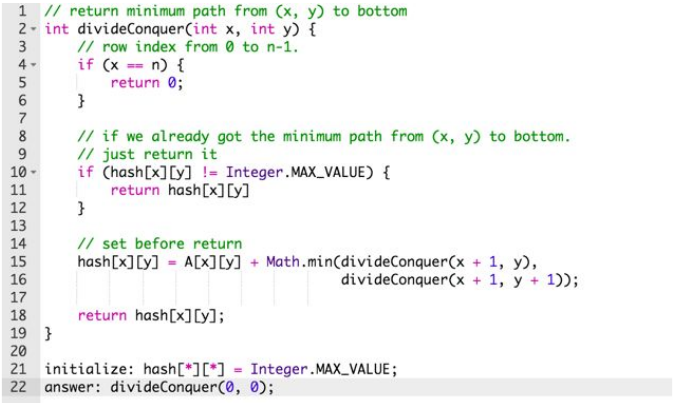
時間複雜度為
其中注意,如果求最小值的時候,初始化往往是int或其型別的最大值;反之如果求最大值,初始化往往為最小值
記憶法的分治時間複雜度計算:
a=一共多少個點
b=每個點處理的時間復雜度
c=每個點訪問幾次
分治法的總時間復雜度=a∗b∗c
此題中的時間複雜度的a為
討論:
動態規劃和分治
1.動態規劃是一種演算法思想,是高於演算法的.而分治的記憶化搜尋是實現動態規劃的一種手段. 2.那麼什麼是動態規劃呢? -就感覺上來說,動態規劃的是"一層一層來",基於前一個狀態推出現在的狀態. 3.動態規劃為什麼會快呢? -因為減少了很多不必要的重複計算. 4.動態規劃和分治的區別? -動態規劃約等於分治+記憶化,因為有了記憶化,所以算過的直接用就行,就不用再算一遍了.
什麼時候使用動態規劃:
動態規劃適合把暴力時間複雜度為指數型的問題轉化為多項式的複雜度,即
1.求最大最小的問題
2.判斷可不可行,存不存在
3.統計方案個數
什麼時候不用動態規劃:
動態規劃不適合把本來時間複雜度就在
1.求!!所有的,具體的!!方案而不是方案個數,要用DFS而不是DP.(100%不用DP)
2.輸入資料是一個集合而非序列(90%不用DP)
動態規劃的實現方式
多重迴圈的兩種方式:
- 自底向上
- 自頂向下
自底向上程式碼如下:

時間複雜度:
空間複雜度:
自頂向上程式碼如下:

時間複雜度依舊:
空間複雜度依舊:
動態規劃的四點要素
1.狀態:即定義,劃分為六大問題
2.方程:即從前一種狀態推出現在的狀態.
3.初始化:極限小的狀態,即為起點.
4.答案:終點
狀態的六大問題:
1.座標型15%
2.序列型30%
3.雙序列型30%
4.劃分型10%
5.揹包型10%
5.區間型5%
初始化的小技巧
沒有左上和右上的提出來先算,也可以說成二維DP問題, [i,0]和[0,i]先初始化.


