Program in Lua中圖演算法的改進(列印所有圖路徑)
阿新 • • 發佈:2019-01-11
在Program in Lua第二版,第11.7節中介紹了用lua寫“圖”資料結構的方法,
但書中提供的圖的演算法只能打印出第一條找到的正確路徑,於是我就自己琢磨
著怎麼用lua寫出一個圖演算法打印出所有可能的路徑,自己獨自一個人思考了
很久,期間沒有參考任何資料,完全靠“頭腦暴力”把它解決了,最後思考了看看,
也不知道這到底是什麼演算法,完全憑藉著自己認為的所謂的"退化"的概念,奇妙
的解決了這個問題,所以我把這個演算法拿出來分享一下。
(總覺得在哪本書上看到過“退化”這個字眼,但我其實不知道什麼是真正的“退化”,
但在我腦海裡,“退化”就是一個概念而已,在這裡,覺得似乎用這個概念有那麼
一點合適的味道,那我就把它稱之為“退化”了。另外,也許這個演算法也有人實現
過,但我其實並不知道這是什麼演算法,我只知道這個演算法的思想---用我所謂的
“退化”(因為我學的很少,至少還沒去專門學過圖論,所以勿噴),如果我這個
”設計“的演算法你見過,或知道是什麼演算法可以告訴我(至少我不認為我能想出來
的東西別人會沒想到,我應該還沒到那種境界吧=_=))
正文:
首先是一個儲存了圖中資料的.lua檔案,其名為graph.lua,
相對路徑為./lua/graph.lua
內容如下所示:
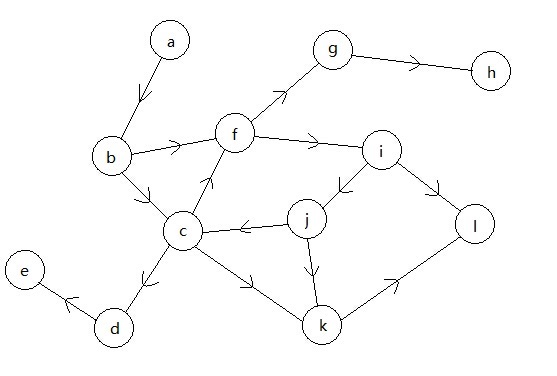
a b b c b f c d c f d e f g g h f i i j j c j k i l c k k l
示意圖如下:
(該演算法只適用於單向的圖)
然後是“圖”資料結構及我“設計”的這個演算法:
相對路徑為./lua/11.7.lua
(註釋寫的很詳細,都寫在程式碼裡面了,不懂的可以問我)
Graph = {} --生成圖節點 function Graph.newNode(graph, name) if not graph[name] then graph[name] = {name = name, adj={}} --建立一個新的圖結點 end return graph[name] end --生成圖 function Graph.gen(s) local graph = {} for line in io.lines(s) do --匹配起始,通往結點 local namefrom, nameto = string.match(line, "(%S+)%s(%S+)") local from = Graph.newNode(graph, namefrom) --生成起始結點 local to = Graph.newNode(graph, nameto) --生成通往結點 local path = from.adj --得到路徑表 path[#path + 1] = to --連線圖結點路徑 end return graph end function Graph.findpath(curr, to, path, visited) --引數:當前結點, 目的結點, 儲存路徑的集合, 已訪問結點集合(可退化) --關於退化:這裡的退化概念是自己提出的,意思是對得到一條通路上的結點 --往前回溯取消記錄,以致於另一個遞迴搜素分支可以找到這條路徑,同時, --對於已壓棧函式記錄的結點和無通路徑上的結點儲存記錄以至於遞迴函式 --直接返回 path = path or {} --path作為table來記錄所有儲存的路徑 visited = visited or {} --visited為儲存記錄結點的表 if visited[curr] then --對記錄結點直接返回 return nil end visited[curr] = true --記錄訪問節點 path["name"] = curr["name"] --記錄路徑 if curr == to then --找到終點,構成一條路徑,返回 visited[curr] = nil --退化(取消該終點的記錄) return path end local p for i,from in ipairs(curr.adj) do path[i] = {father = path} --儲存一個能找到父結點的欄位 --遞迴搜尋路徑 local rightPath = Graph.findpath(from, to, path[i], visited) if not rightPath then path[i] = nil end --找不到,取消一個子table p = rightPath or p --有路徑時記錄最後一條通路返回,否則返回nil end if p then visited[curr] = nil --退化該路徑節點 return p["father"] --返回該路徑的father,即本結點 end path = nil --沒找到,刪除該節點 end --列印所有圖路徑 function Graph.printPath(path, visited) --路徑結點集合, 已訪問結點集合(可退化) path = path or {} visited = visited or {} if path then visited[#visited + 1] = path --以陣列形式儲存訪問過的路徑 io.write(path.name, " ") --列印本結點名字和空格符 end local maxn = table.maxn(path) --取可行支路中的最大編號 if maxn == 0 then --不存在支路(即終點)時 visited[#visited] = nil --退化,取消記錄該結點 io.write("\n") --該條路徑已完全輸出,換行 return end --終點,返回 local count = 0 --統計支路的數目 for i = 1, maxn do if path[i] then --該條編號的支路存在 count = count + 1 --遞增支路數 if count > 1 then --除第一條支路之外, for i,v in ipairs(visited) do --對已記錄的根路結點進行列印 io.write(v.name, " ") end end Graph.printPath(path[i], visited) --然後再次遞迴搜尋下一條支路 end end visited[#visited] = nil --支路已搜尋完畢,此分支不再搜尋,退化 end local graph = Graph.gen("./lua/graph.lua") --生成圖 local path = Graph.findpath(graph["a"], graph["l"]) --尋找圖路徑 Graph.printPath(path) --輸出圖路徑
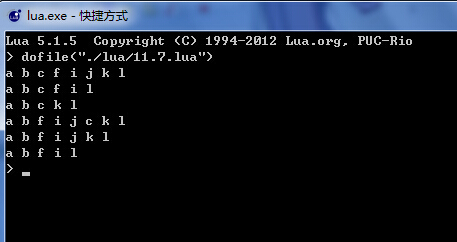
下面是執行後的輸出結果: