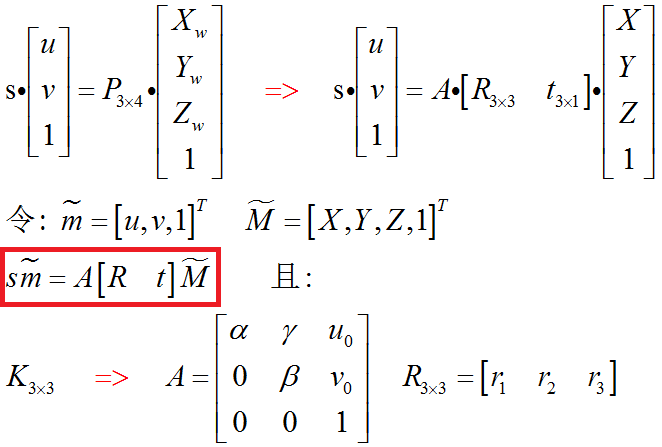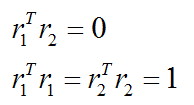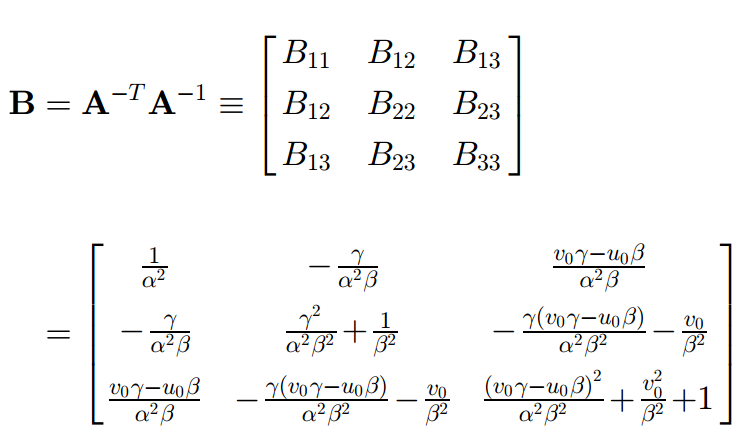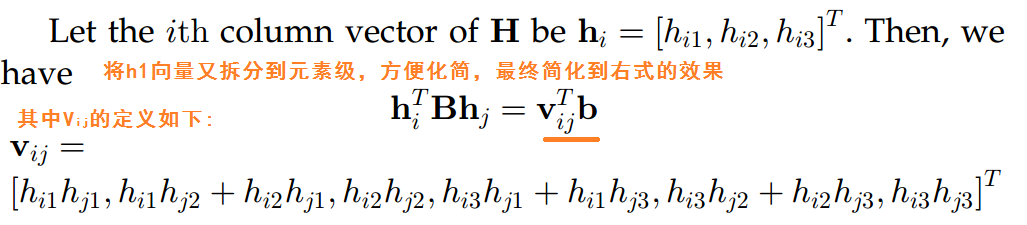相機模型及相機標定原理詳解
相機模型
除進行高精度尺寸測量使用遠心鏡頭外，我們正常使用的相機鏡頭都是普通鏡頭，其成像模型都是理想的小孔成像模型。
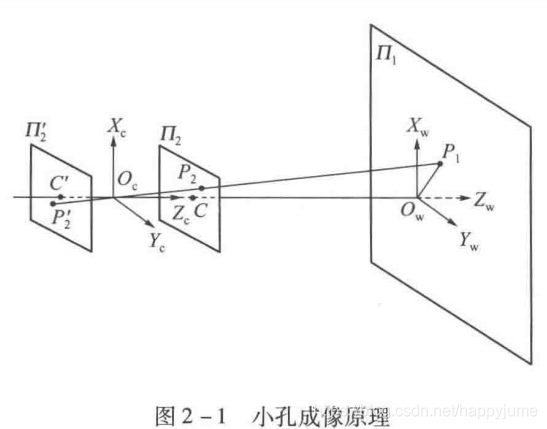
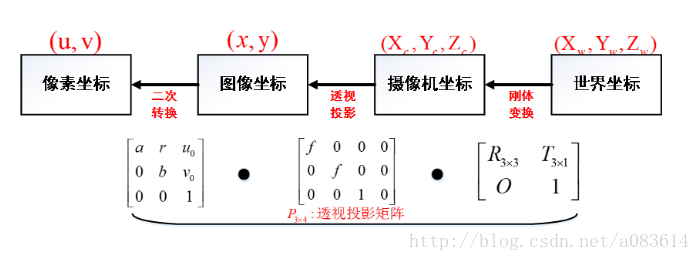
我們在光軸中心處建立座標系，Z軸方向平行於光軸，正方向為相機到拍攝物件的方向，X方向取影象座標系的方向，可以理解為上述平面的X軸。根據上圖，我們可以得到相機模型中重要的幾個座標系：世界座標系
、相機座標系（Xc、Oc、Yc組成）、像平面座標系
，還有畫素座標系。其中像平面座標系
和畫素座標系（u，O0，v）之間的關係如下圖：
像平面座標系的原點在畫素座標系的中間，不考慮像平面座標系和畫素座標系間的縮放，理想情況下（u0，v0）為解析度的1/2。
在相機座標系下，設空間中一點P1的座標為（x1，y1，z1），其在像平面的成像點P2座標為（x2，y2，z2），則有：
其中f為相機的焦距，f = z2。
相機內參模型
相機的內參可以理解描述相機座標系和畫素座標系間的模型。
成像平面上的像經過放大處理得到數字影象，像平面上的成像點（x2，y2）經過轉換成畫素座標系中的（u，v）點，則有:
由此可以得到：
用矩陣的形式表示：
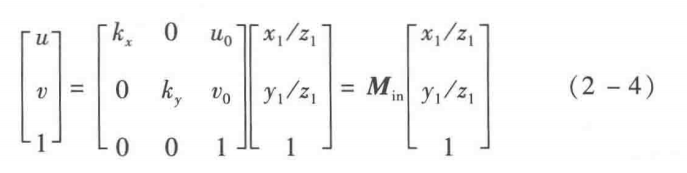
其中：
是x軸方向的放大係數；
是Y軸方向的放大係數；
成為相機的內參矩陣，因其含有4個引數，也稱為相機的四引數模型，也是實際中應用最多的一種模型；（x1，y1，z1）是點在相機座標系下的座標。
一般地，點在相機座標系下用（xc，yc，zc）表示，因此，上式一般改寫為：
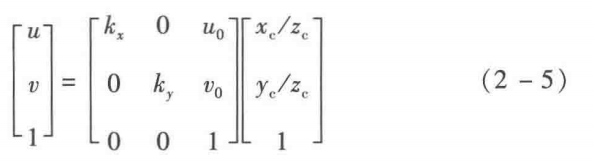
如果考慮放大係數kx與ky的差異和x軸與y軸間的耦合，則構成的相機內參模型具有5個引數，如下：‘
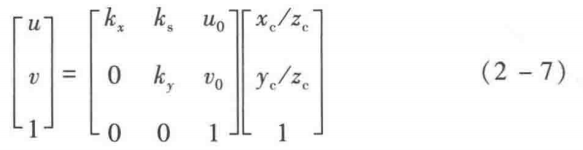
相機外參模型
相機的外參模型是世界座標系在相機座標系中的表示，也可以理解從相機座標系到世界座標系的變換。
熟悉三維座標變換的朋友可以看出，上述外參矩陣可以分為左上角的旋轉矩陣R和右上列隊T，也即相機座標系到世界座標系的RT。
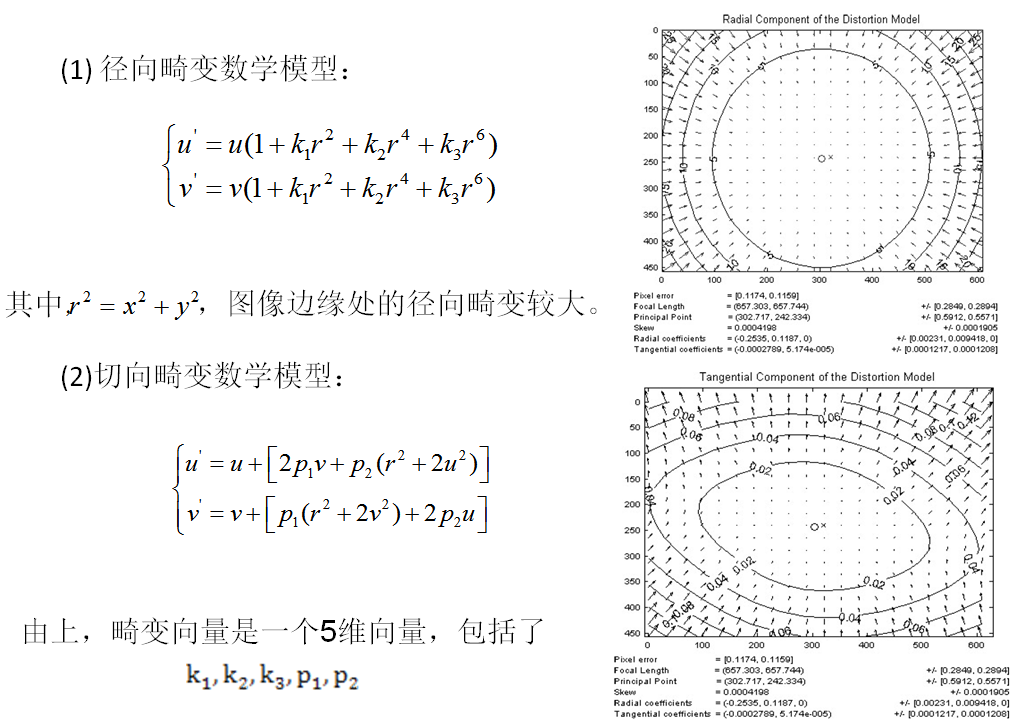
畸變模型
實際成像時，由於鏡頭的製造工藝和裝配誤差等原因，成像時會出現畸變。其中由透鏡的形狀引起的畸變稱為徑向畸變，由相機組裝過程中透鏡和成像面不嚴格平行引起的畸變稱為切向畸變。
相機標定
根據上述介紹，四個與相機模型有關的座標系之間的關係可以用下圖來表示：
也可以這麼說，相機標定的目的就是確定內參、外參和各個畸變係數
關於相機標定，此處搬運別人的部落格（https://blog.csdn.net/humanking7/article/details/44756235）
上述推導的公式可總結如下：
符號規定( Notation )
為了和 張正友教授 的論文相統一，現在把公式符號統一一下。
推導中的數學基礎
第一點 : 旋轉向量 R 為正交矩陣，所以又以下的性質：
第二點 : 就是 S 。它是尺度因子，它的出現只是為了方便運算，而且對於齊次座標，尺度因子不會改變座標值 。
Step.1 標定平面到影象平面的單應性(Homography)
剛開始不知道論文中 Homography 不知道是何方神聖，搜尋到了最後這番解釋：
因為張氏標定是一種基於平面棋盤格的標定，所以想要搞懂張氏標定，首先應該從兩個平面的單應性(Homography)對映開始著手。
單應性(Homography) ： 在計算機視覺中被定義為一個平面到另一個平面的投影對映。首先看一下，影象平面與標定物棋盤格平面的單應性。
因為標定物是平面，所以我們可以把世界座標系構造在 Z = 0 的平面上。然後進行單應性計算。令 Z = 0 可以將上式轉換為如下形式 ( 直接擷取論文中的推導 ) ：
分析：
H 是一個3x3的矩陣，並且有一個元素作為齊次座標。因此，H有8個未知量待解 ( 可以分析一下， A 有5個未知量，後面的 [r1,r2,t] 有三個未知量，一共8個) 。
(X,Y) 作為標定物的座標，可以由設計者人為控制，是已知量 。 (u,v) 是畫素座標，我們可以直接通過攝像機獲得。一組對應的 (X,Y) => (u,v) 我們可以獲得兩組方程。
現在有 8個未知量 待求，所以至少要8個方程。所以至少需要4組對應的點。所以有 4組 (X,Y) => (u,v)就可以算出，影象平面到世界平面的 單應性矩陣H ，這也是張正友標定採用四個角點的棋盤作為標定物的一個原因 (？不知道是否正確) 。
Step.2 利用約束條件求解內參矩陣A
從Step1可知，應用4個點我們可以獲得單應性矩陣H。但是H是內參陣和外參陣的合體。我們想要最終分別獲得內參和外參。所以需要想個辦法，先把內參求出來。然後外參也就隨之解出了。
上式中的 h1,h2 是通過求解單應性矩陣 H 求出來的，所以未知量只剩下 內參矩陣A 。 A中含有5個引數，如果需要完全解出來這5個未知量，則需要 3個不同的單應性矩陣H ( 因為 3個不同的單應性矩陣H在2個約束條件下可以產生6個方程 ) ， 那麼如何得到 3個不同的單應性矩陣H 呢？ 那就是 3張不同的標定平面的照片， 我們大多是通過改變攝像機與標定板間的相對位置來獲得不同的標定照片。( 如果用2張照片進行標定，就要捨去一個內參 r=0)
當然這只是張正友標定法不斷變換標定板方位的 第一個原因 。第二個原因 是張正友提到的 最大似然估計 ( Maximum-Likelihood Estimation ) ( 這個我還得學習 ) 。
現在開始數學課了：
首先令
可以看出 矩陣B 是一個對稱矩陣，有效的元素只有 6個 ，所以令一個 6維的向量b ，然後簡化公式 ( 就是那兩個約束條件 )
將運算的結果帶入到兩個約束條件中，可得到方程組：
英文部分也提出了3張圖片的作用 ( 不懂的可以再看看前面的分析 )
應用上述公式解出b後，就得到了B，在進行 cholesky分解 就可以得到 攝像機內參矩陣A 。
Step.3 利用內參矩陣A求解外參矩陣
已經有了內參矩陣A，通過下面的公式，就可以解出來，外參矩陣了。
參考資料：
《機器人視覺測量與控制》
https://blog.csdn.net/humanking7/article/details/44756235
https://blog.csdn.net/tiantangzixue/article/details/79878996