實驗目的：掌握指標變數、動態變數的含義，掌握二叉樹的結構特徵，以及各種儲存結構的特點及適用範圍，掌握指標型別描述、訪問和處理二叉樹的運算；

實驗原理：參照課本 p.95-107， Figure4.13-4.25；

實驗內容：已知以二叉樹表作為儲存結構，寫出按層次順序遍歷二叉樹的演算法

演算法思想：本演算法採用一個佇列 q，先將二叉樹根節點入佇列，然後退佇列，輸出該節點，若它有左子樹，便將左子樹根節點入佇列；若有右子樹，便將右子樹根節點入佇列，直到佇列空為止。因為佇列的特點是先進先出，從而達到按層次順序遍歷二叉樹的目的。

實驗要求：
1) 實現二叉樹表的層次遍歷演算法，並給出應用。

相關程式碼

/*
 *  預定義錯誤幫助函式
 */
#include <stdio.h>  
#include <stdlib.h>  

#define Error( Str )        FatalError( Str )  
#define FatalError( Str )   fprintf( stderr, "%s\n", Str ), exit( 1 )  

tree.h

/*
 *樹相關函式及結構宣告
 */
#ifndef _Tree_H  

typedef char ElementType;

struct TreeNode;
typedef
 
 struct TreeNode *Position;
typedef struct TreeNode *SearchTree;

SearchTree MakeEmpty(SearchTree T);
Position Find(ElementType X, SearchTree T);
Position FindMin(SearchTree T);
Position FindMax(SearchTree T);
SearchTree Insert(ElementType X, SearchTree T);
SearchTree Delete(ElementType X, SearchTree T);
ElementType Retrieve(Position P);

void
 
 PrintElement(SearchTree T);
void PreOrder(SearchTree T);
void InOrder(SearchTree T);
void PostOrder(SearchTree T);

#endif /* Tree_H */

tree.c

/*
 *相關函式的實現
 */
#include "fatal.h"  
#include "tree.h"  

struct TreeNode
{
    ElementType Element;
    SearchTree Left;
    SearchTree Right;
};

SearchTree
MakeEmpty(SearchTree T)
{
    if (T != NULL)
    {
        MakeEmpty(T->Left);
        MakeEmpty(T->Right);
        free(T);
    }
    return NULL;
}

Position
Find(ElementType X, SearchTree T)
{
    if (T == NULL)
        return NULL;
    if (X < T->Element)
        return Find(X, T->Left);
    else
        if (X > T->Element)
            return Find(X, T->Right);
        else
            return T;
}

/* 對二叉查詢樹的FindMin的遞迴實現 */
Position
FindMin(SearchTree T)
{
    if (T == NULL)
        return NULL;
    else
        if (T->Left == NULL)
            return T;
        else
            return FindMin(T->Left);
}

/* 對二叉查詢樹的FindMax的非遞迴實現 */
Position
FindMax(SearchTree T)
{
    if (T != NULL)
        while (T->Right != NULL)
            T = T->Right;

    return T;
}

SearchTree
Insert(ElementType X, SearchTree T)
{
    if (T == NULL)
    {
        /* Create and return a one-node tree */
        T = malloc(sizeof(struct TreeNode));
        if (T == NULL)
            FatalError("Out of space!!!");
        else
        {
            T->Element = X;
            T->Left = T->Right = NULL;
        }
    }
    else
        if (X < T->Element)
            T->Left = Insert(X, T->Left);
        else
            if (X > T->Element)
                T->Right = Insert(X, T->Right);
    /* Else X is in the tree already;we'll do nothing */

    return T; /* Do not forget this line!!! */
}

SearchTree
Delete(ElementType X, SearchTree T)
{
    Position TmpCell;

    if (T == NULL)
        Error("Element not found");
    else
        if (X < T->Element) /* Go left */
            T->Left = Delete(X, T->Left);
        else
            if (X > T->Element) /* Go Right */
                T->Right = Delete(X, T->Left);
            else /* Found element to be deleted */
                if (T->Left && T->Right) /*Two children */
                {
                    /* Replace with smallest in right subtree */
                    TmpCell = FindMin(T->Right);
                    T->Element = TmpCell->Element;
                    T->Right = Delete(T->Element, T->Right);
                }
                else /* One or zero children */
                {
                    TmpCell = T;
                    if (T->Left == NULL) /* Also handles 0 children */
                        T = T->Right;
                    else if (T->Right == NULL)
                        T = T->Left;
                    free(TmpCell);
                }

    return T;
}

ElementType
Retrieve(Position P)
{
    return P->Element;
}

void
PrintElement(SearchTree T)
{
    printf("%c ", Retrieve(T));
}

void
PreOrder(SearchTree T)
{
    if (T != NULL)
    {
        PrintElement(T);
        PreOrder(T->Left);
        PreOrder(T->Right);
    }
}

void
InOrder(SearchTree T)
{
    if (T != NULL)
    {
        InOrder(T->Left);
        PrintElement(T);
        InOrder(T->Right);
    }

}

void
PostOrder(SearchTree T)
{
    if (T != NULL)
    {
        PostOrder(T->Left);
        PostOrder(T->Right);
        PrintElement(T);
    }
}

main.c

/*
 *程式主函式
 */
#include "tree.h"  
#include <stdio.h>  

int main()
{
    SearchTree T = NULL;
    int i, j, m, n;
    ElementType tmp;
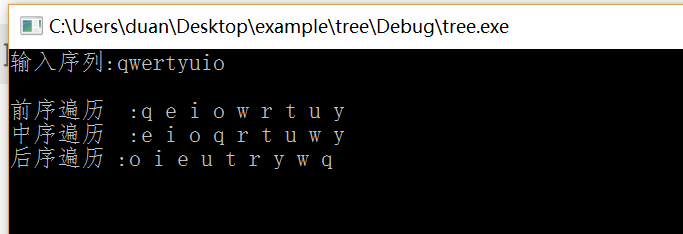
    printf("輸入序列:");
    while (scanf_s("%c", &tmp)) {
        if (tmp == '\n')
            break;
        T = Insert(tmp, T);
    }
    printf("\n前序遍歷  :");
    PreOrder(T);
    printf("\n中序遍歷  :");
    InOrder(T);
    printf("\n後序遍歷 :");
    PostOrder(T);
    printf("\n");
    while (1);
    return 0;
}

結果：

實驗環境 vs2015