二叉樹認識與程式設計實現
歡迎瀏覽我的個人部落格
轉載請註明出處 https://pushy.site
1. 樹
我們都知道,樹是一種一對多的資料結構,它是由n個有限節點組成的一個具有層次關係的集合,它有如下的特點:
- 根節點是唯一的(老大當然是一個~);
- 每個節點都有零個或者必須多個子節點(丁克、獨生子、雙胞胎、三胞胎...);
- 每一個非根節點有且只有一個父節點(只有一個老爹,沒有老王)
如下圖,A即是根節點:
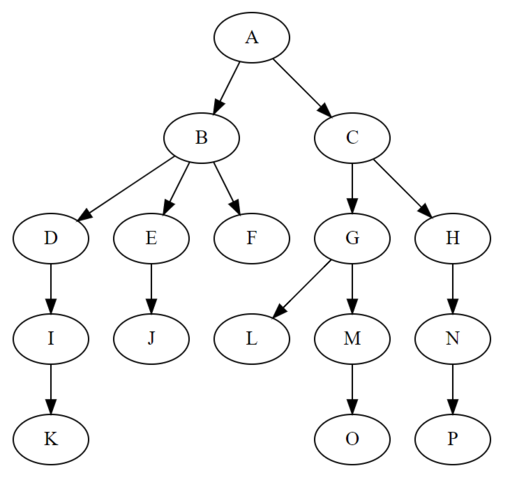
2. 二叉樹
從名字和圖中可以看出,二叉樹應該是一種特殊形式的樹:
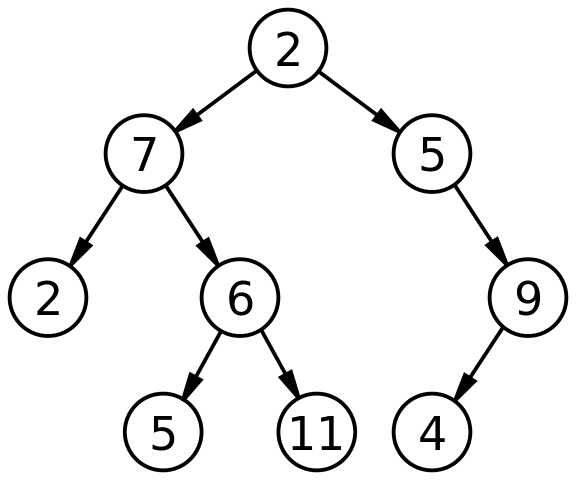
沒錯!它和樹相比,有一下的自己的特點:
每個節點最多有兩顆樹(可以丁克,可以獨生子,可以雙胞胎,但是不允許三胞胎、四胞胎...);
- 左子樹和右子樹是有順序的,次序不能任意顛倒(老大老二分明);
即使樹中的某節點只有一棵子樹,也要區別它是左子樹還是右子樹(獨生子也要稱老大!);
2.1 特殊二叉樹
另外,二叉樹還有特殊的形式:
滿二叉樹:所有分支節點都存在左子樹和右子樹,並且所有的葉子都在同一層上。
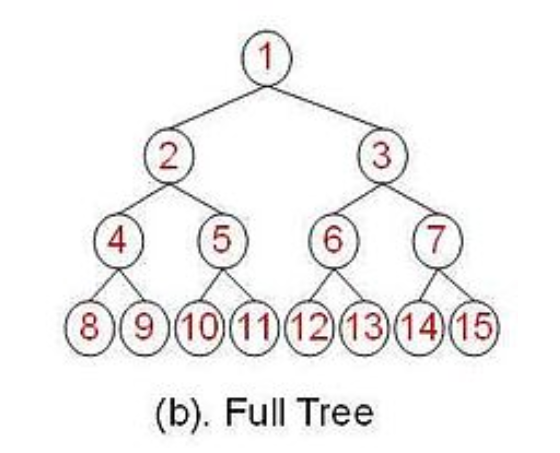
完全二叉樹:在一棵二叉樹中,除最後一層外,若其餘層都是滿的,並且最後一層或者是滿的,或者是在右邊缺少連續若干節點。
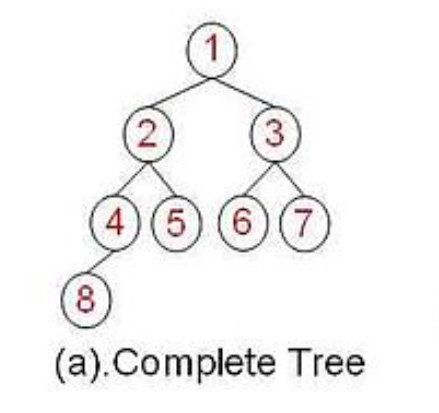
2.2 遍歷方式
先序遍歷
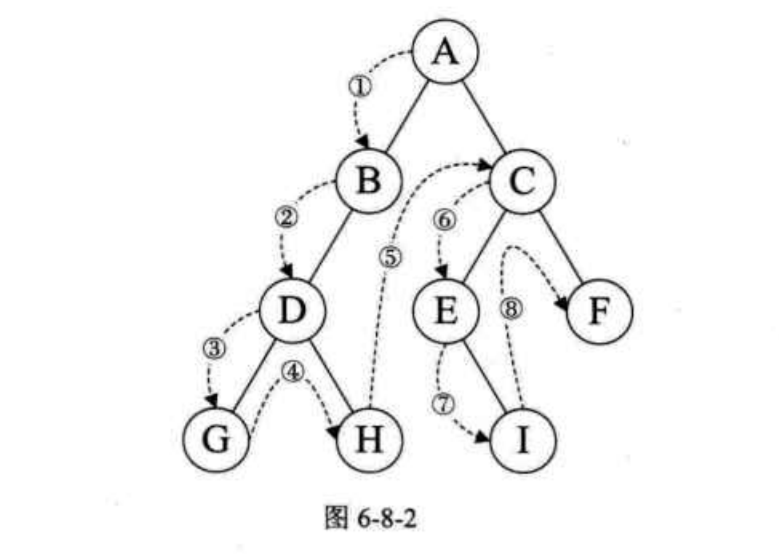
先序遍歷的流程是:若二叉樹為空, 則空操作返回。否則先訪問根節點,然後前序遍歷左子樹,再前序遍歷右子樹。遍歷的順序是:A-B-D-G-H-C-E-I-F
中序遍歷
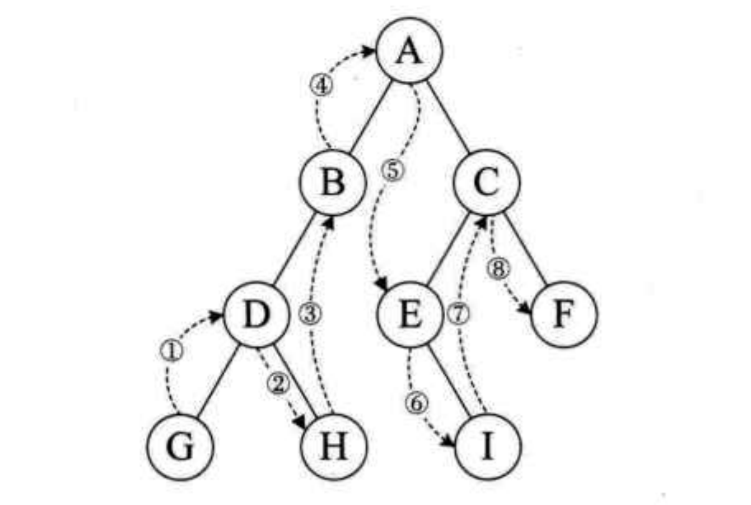
中序遍歷的流程是:若樹為空,則空操作返回,否則從根節點開始(注意並不是先訪問根節點,而是一直找到左子樹的葉子),然後中序遍歷根節點的左子樹,然後是訪問根節點,最後中序遍歷右子樹。遍歷的順序為:G-D-H-B-A-E-I-C-F。
後序遍歷
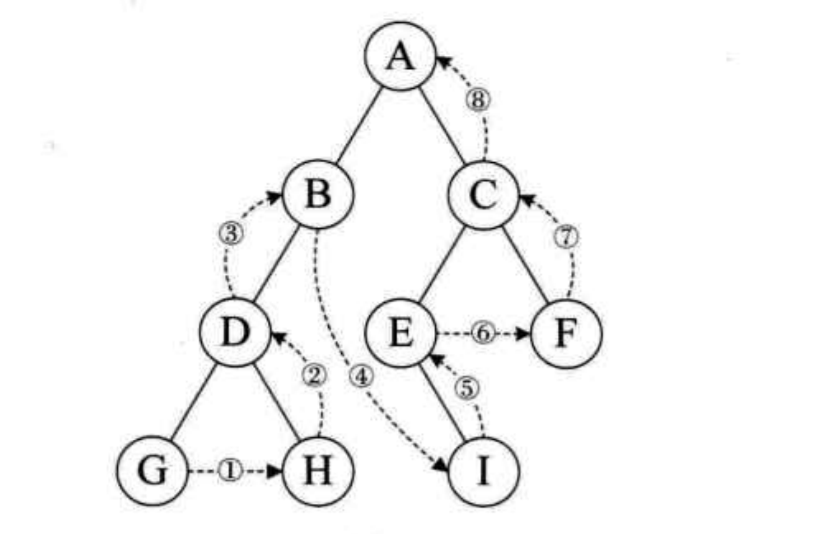
後序遍歷的流程是:若樹為空, 則空操作為空,否則從左到右先葉子後節點的方式遍歷訪問左右子樹,最後是訪問根節點。遍歷的順序為:G-H-D-B-I-E-F-C-A。
3. 程式設計實現
3.1 C
首先來看C語言的實現,定義結構體BiTNode,表示每個結點的結構體。並定義BiTNode型別的指標變數為BiTree:
typedef struct BiTNode { int data; // 資料域 struct BiTNode *lChild; // 左子節點 struct BiTNode *rChild; // 右子節點 } BiTNode; typedef BiTNode* BiTree;
然後定義CreateBiTree,通過先序遞迴的方法來建立二叉樹。當輸入的值為-1時代表當前建立的節點無左子節點或者右子節點:
void CreateBiTree(BiTree *T) {
TElementType ch;
scanf("%d", &ch);
if (ch == -1) {
*T = NULL;
return;
}
else
{
*T = (BiTree) malloc(sizeof(BiTNode)); // 申請記憶體空間,為BiTNode大小
(*T)->data = ch; // 設定資料域的值為輸入的值
printf("輸入%d的左子節點:",ch);
CreateBiTree(&(*T)->lChild); // 遞迴呼叫,構造左子樹
printf("輸入%d的右子節點:",ch);
CreateBiTree(&(*T)->rChild); // 遞迴呼叫,構造右子樹
}
}遍歷的方式是從根節點開始遍歷,先訪問左子節點,該訪問左子節點的左子節點,直到訪問的左子節點的左子節點為空(T==NULL)。然後依次返回上一次遞迴呼叫的地方,開始訪問右節點。直到返回到第一次遞迴呼叫的地方,開始訪問根節點的右子節點,並開始遞迴呼叫訪問。
因此在遍歷的方法中,我們可以反覆地遞迴呼叫PreOrderTraverse來遍歷二叉樹的所有子節點:
void PreOrderTraverse(BiTree T) {
if (T == NULL) {
return;
}
printf("%d", T->data);
// 遞迴呼叫,從根節點的左節點開始遍歷
PreOrderTraverse(T->lChild);
PreOrderTraverse(T->rChild);
}同理,我們可以通過遞迴的方式來實現中序遍歷二叉樹:
void InOrderTraverse(BiTree T) {
if (T == NULL) {
return;
}
InOrderTraverse(T->lChild);
printf("%d", T->data);
InOrderTraverse(T->rChild);
}後序遍歷也一樣:
void PostOrderTraverse(BiTree T) {
if (T == NULL) {
return;
}
PostOrderTraverse(T->lChild);
PostOrderTraverse(T->rChild);
printf("%d", T->data);
}3.2 Java
利用Java面向物件的特點,我們能更簡單地實現二叉樹的結構。首先定義節點類Node,left和right是對左子節點和右子節點的引用:
static class Node {
public Integer data; // 資料域,當前節點儲存的數值
public Node left;
public Node right;
public Node(Integer data) {
this.data = data;
}
}定義BinaryTree類,提供createTree靜態方法進行手動建立根節點,並建立該根節點的左子節點和右子節點,並新增到根節點的引用,最後返回該根節點。
先序遞迴遍歷的方法和C語言實現的差不多:
public class BinaryTree {
/**
* 測試建立二叉樹
*/
public static Node createTree() {
Node root = new Node(1);
Node headLeft = new Node(2); // 建立左節點
Node headRight = new Node(3); // 建立右節點
root.left = headLeft; // 新增引用
root.right = headRight;
return root;
}
/**
* 遞迴實現先序遍歷二叉樹
*/
public static void preOrderTraverse(Node node) {
if (node == null) {
return;
}
System.out.print(node.data);
preOrderTraverse(node.left);
preOrderTraverse(node.right);
}
}另外,我們還可以不使用遞迴,而是使用棧來實現先序遍歷二叉樹的所有節點。實現的原理是:首先將根節點丟入棧中,每次都取出棧頂節點,如果存在右子節點或者左子節點則放入棧中。需要注意的是,必須是先將右子節點放入棧中,因為先序遍歷的話輸出的時候左節點優先於右節點輸出。
這種遍歷的方式稱之為深度優先遍歷,即從根節點出發,沿著左子樹方向進行縱向遍歷,直到找到葉子節點為止。然後回溯到前一個節點,進行右子樹節點的遍歷,直到遍歷完所有可達節點為止。
/**
* 深度優先遍歷,相當於先序遍歷
* 使用棧非遞迴實現二叉樹的遍歷
*/
public static void DFS(Node root) {
if (root == null) {
return;
}
Stack<Node> nodes = new Stack<>();
nodes.add(root);
while (!nodes.isEmpty()) {
// 取出棧頂元素,判斷是否有子節點
Node temp = nodes.pop();
System.out.println("當前子節點的值: " + temp.data);
if (temp.right != null) {
nodes.push(temp.right);
}
if (temp.left != null) {
nodes.push(temp.left);
}
}
}如果你聽說過深度優先遍歷(DFS),那你肯定也知道廣度優先遍歷(BFS),它是從根節點出發,在橫向遍歷二叉樹層段節點的基礎上縱向遍歷二叉樹的層次。下邊我們需要藉助佇列的資料結構來實現廣度優先遍歷:
/**
* 廣度優先遍歷
* 使用佇列非遞迴的方式實現二叉樹的遍歷
*/
public static void BFS(Node root) {
if (root == null) {
return;
}
Queue<Node> nodes = new ArrayDeque<>();
nodes.add(root);
while (!nodes.isEmpty()) {
Node temp = nodes.remove();
System.out.println("當前的子節點為: " + temp.data);
if (temp.left != null) {
nodes.add(temp.left);
}
if (temp.right != null) {
nodes.add(temp.right);
}
}
}維基百科上有一張動圖能很好地展示出廣度優先遍歷的過程:

白色代表尚未加入佇列且未遍歷,灰色代表加入佇列等待遍歷,黑色則代表已經被遍歷。
最後,儘管程式碼在文中基本給出,但是還是準備了一個小demo。因為我個人看博文的話,如果沒有給出一個完整的demo,感覺很難受QAQ...
