鋪地磚-中國石油大學oj(程式碼待補)
阿新 • • 發佈:2019-01-11
鋪地磚
題目描述
一天,晨晨的數學老師佈置了一道題目,大意如下:用1×1和2×2的磁磚不重疊地鋪滿n×3的地板,共有多少種方案?
例如:n=1時:1×3的地板方法就一個,直接由三個1×1的磁磚鋪滿.n=2時:2×3的地板可以由下面3種方案鋪滿:
輸入
第一行:一個整數n(1≤n≤100)。
輸出
輸出鋪滿n×3的地板的方案數。
樣例輸入
樣例資料
3
樣例輸出
5
提示
對於20%的資料,1≤n≤15;
對於50%的資料,1≤n≤30;
對於100%的資料,1≤n≤100;
解析
先設一個f[i]表示i* 3的地板鋪的方法,f[1]=1;f[2]=3
i* 3的地板數是這樣得到的:
(i-1)* 3的地板比i* 3的地板少的地方全鋪上1* 1的瓷磚,只有一種鋪法;或者在(i-2)* 3的地板比i* 3的地板少的地方鋪上2* 2的瓷磚和2個1* 1的瓷磚,這有兩種鋪法
所以得到遞推式:f[i]=f[i-1]+2* f[i-2];
於是乎.得到了遞推式,我們就可以愉快的解決這個題了不存在的.
然後算一算髮現超int了,那就換long long,發現還是超,換unsigned long long,發現又在n=62:3074457345618258603炸了.
emm,nice,所以suo要用大數板子.
不會
於是看了一下遞推式,嗯,齊次的,可以套特徵方程.
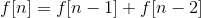
化為

解得
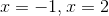
然後套入特徵方程得
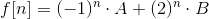
根據f[1]和f[2]的值我們可以解出A和B的值
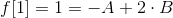
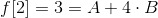
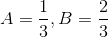
隨後再把A,B的值帶回f[n]求得f[n]的特徵方程為:
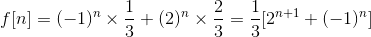
然後只要求解2n+1的值就可以解決問題了
於是…可以選擇特徵方程解決問題,也可以用遞推公式解決問題.
