增廣路定理：用未蓋點表示不與任何匹配邊鄰接的點，其他點位匹配點，即恰好和一條匹配邊臨界的點。從未蓋點出發，依次經過非匹配邊，匹配邊，非匹配邊，匹配邊。。。所得到的路徑稱為交替路。注意，如果交替路的終點時一個未蓋點，則稱這條交替路位一條增廣路。在增廣路中，非匹配邊比匹配邊多一條。增廣路的作用是改進匹配。如果有一條增廣路，那麼把此路上的匹配邊和非匹配邊互換，得到的匹配比剛才多一邊。反過來，如果找不到增廣路，則當前匹配就是最大匹配。

查詢增廣路，存在增廣路就交換增廣路上的非匹配邊和匹配邊，這樣會使得當前最大匹配數+1。

DAG的最小路徑覆蓋

定義：在一個有向圖中，找出最少的路徑，使得這些路徑經過了所有的點。

最小路徑覆蓋分為最小不相交路徑覆蓋和最小可相交路徑覆蓋。

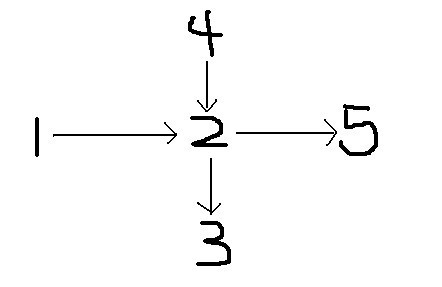
最小不相交路徑覆蓋：每一條路徑經過的頂點各不相同。如圖，其最小路徑覆蓋數為3。即1->3>4，2，5。

最小可相交路徑覆蓋：每一條路徑經過的頂點可以相同。如果其最小路徑覆蓋數為2。即1->3->4，2->3>5。

特別的，每個點自己也可以稱為是路徑覆蓋，只不過路徑的長度是0。

DAG的最小不相交路徑覆蓋

演算法：把原圖的每個點V拆成VxVx和VyVy兩個點，如果有一條有向邊A->B，那麼就加邊A

證明：一開始每個點都是獨立的為一條路徑，總共有n條不相交路徑。我們每次在二分圖裡找一條匹配邊就相當於把兩條路徑合成了一條路徑，也就相當於路徑數減少了1。所以找到了幾條匹配邊，路徑數就減少了多少。所以有最小路徑覆蓋=原圖的結點數-新圖的最大匹配數。

因為路徑之間不能有公共點，所以加的邊之間也不能有公共點，這就是匹配的定義。

//
//  main.cpp
//  POJ1422最小不想交路徑覆蓋
//
//  Created by beMaster on 16/4/8.
//  Copyright © 2016年 beMaster. All rights reserved.
//

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <vector>
using namespace std;
const int N = 200 + 10;
vector<int> g[N];
int cy[N];
bool vis[N];
bool dfs(int u){
    for(int i=0; i<g[u].size(); ++i){
        int v = g[u][i];
        if(vis[v]) continue;
        vis[v] = true;
        if(cy[v]==-1 || dfs(cy[v])){
            cy[v] = u;
            return true;
        }
    }
    return false;
}
int solve(int n){
    int ret = 0;
    memset(cy, -1, sizeof(cy));
    for(int i=1;i<=n;++i){
        memset(vis, 0, sizeof(vis));
        ret += dfs(i);
    }
    return n - ret;
}
int main(int argc, const char * argv[]) {
    int t,n,m;
    int u,v;
    scanf("%d",&t);
    while(t--){
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;++i)
            g[i].clear();
        for(int i=0;i<m;++i){
            scanf("%d%d",&u,&v);
            g[u].push_back(v);
        }
        
        int ans = solve(n);
        printf("%d\n",ans);
    }
    return 0;
}
 

DAG的最小可相交路徑覆蓋

演算法：先用floyd求出原圖的傳遞閉包，即如果a到b有路徑，那麼就加邊a->b。然後就轉化成了最小不相交路徑覆蓋問題。

證明：為了連通兩個點，某條路徑可能經過其它路徑的中間點。比如1->3->4，2->4->5。但是如果兩個點a和b是連通的，只不過中間需要經過其它的點，那麼可以在這兩個點之間加邊，那麼a就可以直達b，不必經過中點的，那麼就轉化成了最小不相交路徑覆蓋。

//
//  main.cpp
//  POJ2594最小可相交路徑覆蓋
//
//  Created by beMaster on 16/4/8.
//  Copyright © 2016年 beMaster. All rights reserved.
//

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <vector>
using namespace std;
const int N = 500 + 10;
bool dis[N][N];
bool vis[N];
int cy[N];
void floyd(int n){
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j)
            for(int k=1;k<=n;++k)
                if(dis[i][k] && dis[k][j])//傳遞可達性
                    dis[i][j] = true;
}
bool dfs(int u, int n){
    for(int i=1;i<=n;++i){
        if(!vis[i] && dis[u][i]){
            vis[i] = true;
            if(cy[i]==-1 || dfs(cy[i], n)){
                cy[i] = u;
                return true;
            }
        }
    }
    return false;
}
int solve(int n){
    int cnt = 0;
    memset(cy,-1,sizeof(cy));
    for(int i=1;i<=n;++i){
        memset(vis,0,sizeof(vis));
        cnt += dfs(i, n);
    }
    return n - cnt;
}
int main(int argc, const char * argv[]) {
    int n,m;
    int a,b;
    while(scanf("%d%d",&n,&m),n+m){
        for(int i=1;i<=n;++i)
            for(int j=1;j<=n;++j)
                dis[i][j] = false;
        for(int i=1;i<=m;++i){
            scanf("%d%d",&a,&b);
            dis[a][b] = true;
        }
        floyd(n);
        int ans = solve(n);
        printf("%d\n",ans);
    }
    return 0;
}

最小路徑覆蓋問題值得注意的問題

首先，最小路徑覆蓋=總節點數-最大匹配數。這個應該已經是路人皆知了。

所謂最小路徑覆蓋，是指在一個有向圖中，找出最少的幾條路徑，用它們來覆蓋全圖

這裡說的值得注意的地方，如果有向圖的邊有相交的情況，那麼就不能簡單的對原圖求二分匹配了

舉個例子，假設有圖：1->2    2->5     2->3      4->2，事實上，這其實就是兩條邊：1->5 4->3 ，節點2只是他們的一個交點

如果只是簡單的在原圖的基礎上求二分匹配，那麼得到的匹配答案是2，最小路徑覆蓋答案便是5-2=3。

可是隨便一看都能看看出端倪，這個圖中，只需要兩個點便可以探索完整個地圖，這裡最小路徑覆蓋數明顯是2。

問題究竟出在哪裡呢？其實就和這個交點2有關。既然邊有相交，那麼他們的連通性也應該連通下去。

解決的辦法是對原圖進行一次閉包傳遞(也就是flody)，於是便增加了四條邊:1->3  1->5   4->3  4->5

這時再求最大匹配數，匹配答案便是3，最小路徑覆蓋值為2，這是正確答案！