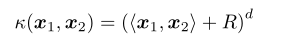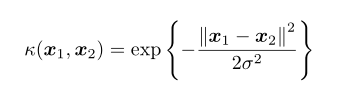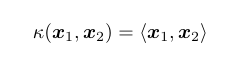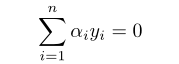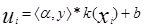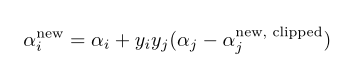支援向量機SVM(Support Vector Machine)是一種有監督的學習模型，它的核心有兩個：一、核函式(kernel trick)；二、序列最小優化演算法SMO（Sequential minimal optimization）是John Platt在1996年釋出的用於訓練SVM的有效演算法。本文不打算細化SVM支援向量機的詳細推倒演算法，只涉及以上兩點的內容做一個說明，最後給出演算法實現和一個實驗對比圖。

核函式

核函式在處理複雜資料時效果顯著，它的做法是將某一個維度的線性不可分資料採取核函式進行特徵空間的隱式對映到高維空間，從而在高維空間將資料轉化為線性可分，最後迴歸到原始維度空間實施分類的過程，常見的幾個核函式如下：

多項式核：

高斯核（徑向基函式）:

線性核：

即是兩個矩陣空間的內積。

SMO演算法流程

SMO的主要兩個步驟就是：

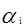
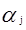
1、選擇需要更新的一對和，採取啟發式的方式進行選擇，以使目標函式最大程度的接近其全域性最優值；

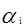
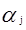
2、將目標函式對和進行優化，以保持其它所有α不變。

以上是兩個基本步驟，實現具體推到公式如下：

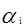所需要收到的約束條件為：

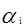
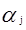
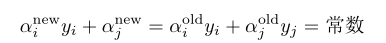
同時更新和，要求滿足如下條件，就可以保證為0的約束

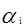
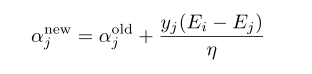
消去可得

其中

的表示式為：

為第i個特徵因素的真實標籤值

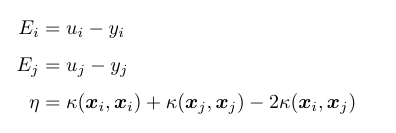
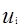
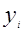
之後考慮約束條件則

約束條件的線性表示

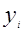
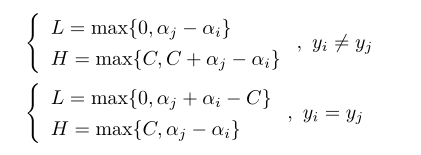
依據和同號或是異號，可得出上下兩個邊界為

對於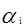有

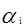
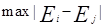
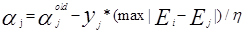
對於首先可以通過求得j，之後計算方式可為

而b的更新為

其中

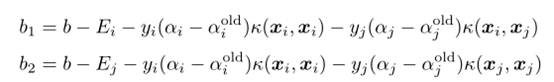
每次更新完和都需要重新計算b以及對應的和

有了以上的公式，程式碼實現就比較簡單了。

演算法實現

完整的Platt-smo演算法實現入口

public SvmResult plattSmo(final SvmResult svmResult) {
		double b = svmResult.getB();
		double[] alphas = svmResult.getAlphas();
		
		for(int i=0;i<featuresArray.length;i++){
				double ei = this.calcEk(i, alphas, b);
				if (((lablesArray[i] * ei < -tolerFactor)
						&& (alphas[i] < penaltyFactor))
						|| ((lablesArray[i] * ei > tolerFactor) && (alphas[i] > 0))) {
					double[] jSelected = this.selectJ(i, ei, alphas, b); //啟發式實現j的選擇
					int j = (int) jSelected[0]; 
					double ej = jSelected[1];
					double alphaIold = alphas[i];
					double alphaJold = alphas[j];
					double L = 0;
					double H = 0;
					//邊界計算
					if (lablesArray[i] != lablesArray[j]) {
						L = Math.max(0, alphas[j] - alphas[i]);
						H = Math.min(penaltyFactor, penaltyFactor + alphas[j]
								- alphas[i]);
					} else {
						L = Math.max(0, alphas[j] + alphas[i] - penaltyFactor);
						H = Math.min(penaltyFactor, alphas[j] + alphas[i]);
					}
					if (L == H) {
						logger.info("L==H");
					} else {
						double eta = (2.0 * this.kernelArray[i][j] - this.kernelArray[i][i] - this.kernelArray[j][j]);
						if (eta >= 0) {
							logger.info("eta>=0");
						} else {
							//雙向調整alphas[j]遞減
							alphas[j] -= lablesArray[j] * (ei - ej) / eta;
							if (alphas[j] > H) {
								alphas[j] = H;
							}
							if (L > alphas[j]) {
								alphas[j] = L;
							}
							//更新ej
							this.updateEk(j, alphas, b);
							if (Math.abs(alphas[j] - alphaJold) < 0.00001) {
								logger.info("j not moving enough");
							} else {
								//雙向調整alphas[i]遞減
								alphas[i] += lablesArray[j] * lablesArray[i]
										* (alphaJold - alphas[j]);
								//更新ei
								this.updateEk(i, alphas, b);
								//計算b
								double b1 = b - ei- lablesArray[i]*(alphas[i]-alphaIold)*this.kernelArray[i][i] - lablesArray[j]*(alphas[j]-alphaJold)*this.kernelArray[i][j];
								double b2 = b - ej- lablesArray[i]*(alphas[i]-alphaIold)*this.kernelArray[i][j] - lablesArray[j]*(alphas[j]-alphaJold)*this.kernelArray[j][j];
								if ((0 < alphas[i]) && (penaltyFactor > alphas[i])){
									b = b1;
								}else if ((0 < alphas[j]) && (penaltyFactor > alphas[j])){
									b = b2;
								}else{
									b = (b1 + b2)/2.0;
								}
								
							}
						}
					}
				}
		}
		return new SvmResult(b, alphas);
	}
 

在以上演算法裡面重點關注是j的選擇，

J的選擇

private double[] selectJ(int i,double ei,double[] alphas,double b){
		int maxK = -1; 
		double maxDeltaE = 0; 
		double ej = 0;
		int j = -1;
		double[] eiArray= new double[2];
		eiArray[0] = 1d;
		eiArray[1] = ei;
		this.eCache[i] = eiArray;
		boolean hasValidEcacheList = false;
		for(int k=0;k<this.eCache.length;k++){
			if(this.eCache[k][0] > 0){
				if(k == i){
					continue;
				}
				hasValidEcacheList = true;
				if(k == this.m){
					k = m-1;
				}
				double ek = this.calcEk(k, alphas, b);
				double deltaE = Math.abs(ei - ek);
				if (deltaE > maxDeltaE){
	                maxK = k; 
	                maxDeltaE = deltaE; 
	                ej = ek;
				}
			}
		}
		j = maxK;
		if(!hasValidEcacheList || j == -1){
			j = this.selectJRandom(i);
			ej = this.calcEk(j, alphas, b); 
		}
		if(j == this.m){
			j = m-1;
		}
		return new double[]{j,ej};
	}
 

首選採取啟發式選擇j，通過計算deltaE的最大值來逼近j的選擇，如果選擇不到就隨機選擇一個j值，在j選擇裡面有一個Ek的計算方式

private double calcEk(int k,double[] alphas,double b){
		Matrix alphasMatrix = new Matrix(alphas);
		Matrix lablesMatrix = new Matrix(lablesArray);
		Matrix kMatrix = new Matrix(this.kernelArray[k]);
		double fXk = alphasMatrix.multiply(lablesMatrix).dotMultiply(kMatrix.transpose()).dotValue() + b;
		double ek = fXk - (float)this.lablesArray[k];
		return ek;
	}

下面再介紹一下核函式計算方式，本文主要採取徑向基函式(RBF)實現，如下

public double[] kernelTrans(double[][] featuresArray,double[] featuresIArray){
		int mCount = featuresArray.length;
		double[] kernelTransI = new double[mCount];
		Matrix featuresMatrix = new Matrix(featuresArray);
		Matrix featuresIMatrix = new Matrix(featuresIArray);
		if(trainFactorMap.get("KT").equals("lin")){
			Matrix result = featuresMatrix.dotMultiply(featuresIMatrix.transpose());
			kernelTransI = result.transpose().values()[0];
		}else if(trainFactorMap.get("KT").equals("rbf")){
			double rbfDelta = (double)trainFactorMap.get("rbfDelta");
			for(int j=0;j<mCount;j++){
				Matrix xj = new Matrix(featuresArray[j]);
				Matrix delta = xj.reduce(featuresIMatrix);
				double deltaValue = delta.dotMultiply(delta.transpose()).dotValue();
				kernelTransI[j] = Math.exp((-1.0*deltaValue)/(2*Math.pow(rbfDelta, 2)));
			}
		}
		return kernelTransI;
	}

最後看下測試程式碼實現

double[][] datasvs = new double[m][d[0].length];
			double[] labelsvs = new double[m];
			double[] alphassvs = new double[m];
			int n = 0;
			for(int i=0;i<alphas.length;i++){
				if(alphas[i] != 0){
					datasvs[n] = d[i];
					labelsvs[n] = l[i];
					alphassvs[n] = alphas[i];
					n++;
				}
			}
			
			//model test
			int errorCount = 0;
			for(int i=0;i<d.length;i++){
				double[] kernelTransI = learner.kernelTrans(datasvs, d[i]);
				Matrix kernelTransIM = new Matrix(kernelTransI);
				Matrix labelsvsM = new Matrix(labelsvs);
				Matrix alphassvsM = new Matrix(alphassvs);
				double predict = kernelTransIM.dotMultiply(labelsvsM.multiply(alphassvsM).transpose()).dotValue() + b;
				System.out.println(i+"\t"+predict+"\t"+l[i]);
				if(AdaBoost.sigmoid(predict) != l[i]){
					errorCount++;
				}
			}

測試程式碼是首先找出所有的支援向量，並提取支援向量下的特徵向量和標籤向量，採取核函式進行隱式對映，最後計算預測值。

訓練結果

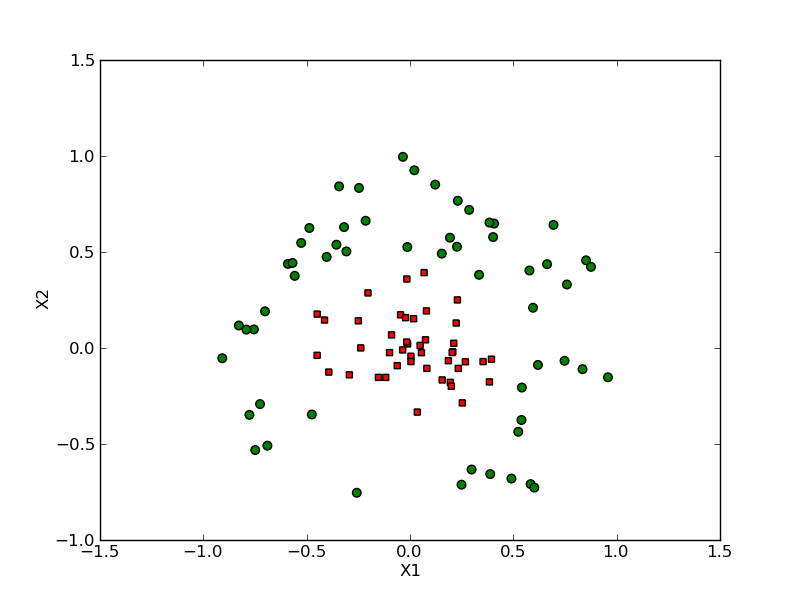
本文采取100個二維平面無法線性可分的資料集合，如下

通過徑向基函式對映後採取支援向量預測計算得到的可分平面如下

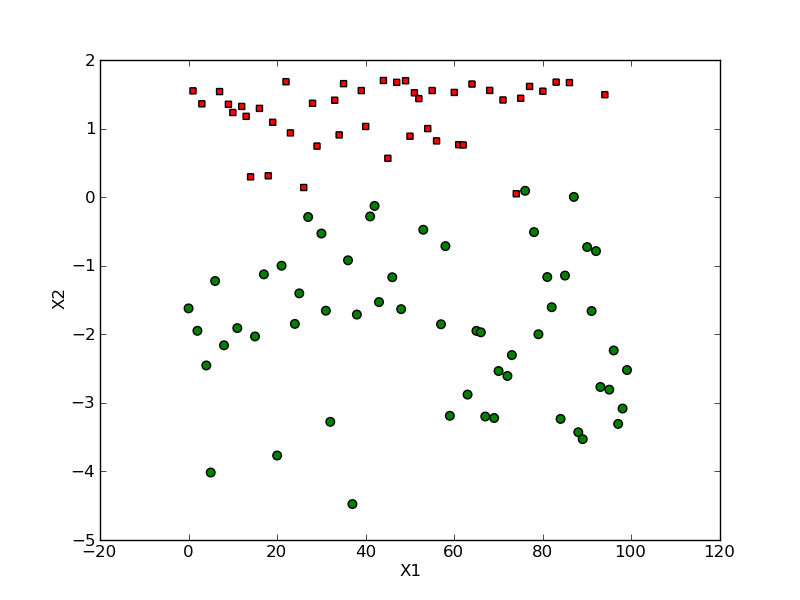
本演算法100個數據訓練準確率可達98%。

注：本文演算法均來自Peter Harrington的《Machine Learning in action》