五類八個排序比較+實現+詳細解釋
前言
剛學完資料結構,寫此文目的如下
- 加深對五大類共八個排序演算法思想的理解
- 比較各自的演算法效率(主要是時間複雜度)
- 尋找演算法思想間的聯絡與區別
- 用順序結構、鏈式結構實現演算法
- 用遞迴、非遞迴(迭代)實現演算法
- 記錄下來以便複習鞏固
(五類排序演算法思維導圖)
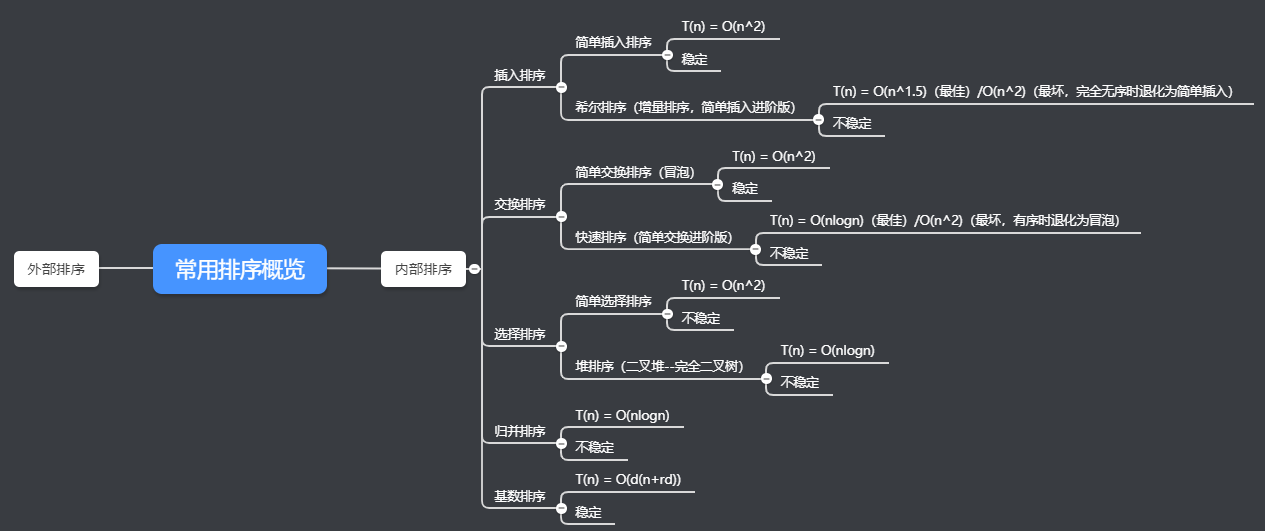
穩定性: 舉個例子,假如我們要對序列A進行排序,排序前A中存在兩個元素a1,a2,這兩個元素滿足同時條件1,a1=a2;條件2,a1在a2之前。若是在排好序的A’中a1依舊在a2之前,那麼,我們可以稱其滿足穩定性。
一句話,穩定性就是遵循先來後到的原則
總結並補充上圖:
1,常用排序有五大類,每一類中都是先出現簡單,符合人思維的演算法,為了提高效率,大家在此前基礎上改進演算法,進而出現了高效的演算法。可見演算法的發展是循序漸進,迭代而成,因此,若是按照其發展脈絡學習演算法,更容易理解演算法間的關係
2,簡單插入、交換、基數排序滿足穩定性,其餘皆不穩定
3,希爾排序效率與增量選取有關
4,堆排序有大、小頂堆之分。升序建大頂堆;降序建小頂堆
本文均以升序為例
資料結構
採用順序結構,為了程式通用性,使用動態陣列
typedef struct
{
int *elem;//陣列首地址
int length;//陣列長度
}SqList;
//初始化動態陣列
void InitSqList(SqList &L)//記得加引用,賦初值才有效
{
L.elem = NULL;
L.length = 0;
}
自定義佇列及其基本操作
//佇列資料結構
typedef struct QNode
{
int data;
struct QNode* next;
}QNode,LNode,*LinkList;
typedef 前期準備函式
- 由於使用檔案交換資料,所以需設計檔案儲存、讀取、重讀取函式;隨機產生不超過五位的非負整數
- 由於兩個元素間交換頻繁,因此設計元素交換函式
//建立動態陣列
void CreateSqList(SqList &L)//記得加引用
{
L.length = N;//N是巨集定義,表示元素個數
L.elem = (int*)malloc(N*sizeof(int));//動態陣列必須分配記憶體!!!!!
fstream inFile("Sort.dat",ios::binary | ios::in);//以只讀二進位制方式儲存檔案
inFile.read((char*)L.elem,N*sizeof(int));
inFile.close();//記得關閉
}
//重新載入動態陣列,以相同的資料測試新的排序演算法
void ReloadSqList(SqList &L)
{
if(L.elem != NULL)
{
L.length = N;
// L.elem = (int*)malloc(N*sizeof(int));//動態陣列必須分配記憶體!!!!!
fstream inFile("Sort.dat",ios::binary | ios::in);//以只讀二進位制方式儲存檔案
inFile.read((char*)L.elem,N*sizeof(int));//二進位制讀取,直接覆蓋L之前的元素
inFile.close();//記得關閉
}
}
//把隨機數以二進位制形式存入檔案。每次直接寫會覆蓋之前的內容
void CreateRandFile()//檔案流無法作為引數???或許是因為檔案可以在任何處被開啟,可看做全域性陣列
{
SqList L;//中間儲存
InitSqList(L);
L.length = N;
L.elem = (int*)malloc(N*sizeof(int));
srand((int)time(0));//隨機數種子
for(int i = 0; i < N; i++)
{
L.elem[i] = rand()%100000;//保證產生5位數以內,為桶排序準備
}
fstream outFile("Sort.dat",ios::binary | ios::out);//以只寫二進位制方式儲存檔案
outFile.write((char*)L.elem,N*sizeof(int));
outFile.close();//記得關閉讀,下次再開啟讀指標從頭開始
free(L.elem);//記得釋放
}
//交換
void swap(int &a, int &b)//記得加引用,否則傳入的引數在此函式結束後不會改變
{
int t = a;
a = b;
b = t;
}
//僅僅為測試從檔案讀取資料是否成功,排序是否成功
void TraverseSqList(SqList L)
{
for(int i = 0; i < L.length; i++)
{
cout<<L.elem[i]<<" ";
}
}
插入排序
簡單插入排序
演算法思想
一個元素插入一個有序序列L,新序列L’依舊有序
演算法描述
1,初始狀態:第一個元素預設已有序,加入有序序列L
2,將距離序列L最近的元素插入L,得到新的有序序列L
3,重複步驟2,直到所有元素均在L中
演算法實現(C++)
//=========================簡單插入排序============================
//簡單插入排序,從第二個開始
void InsertSort(SqList L)
{
for(int i = 1; i < L.length; i++)//從第二個開始
{
for(int j = i; j > 0; j--)
{
if(L.elem[j] < L.elem[j-1])
{
swap(L.elem[j],L.elem[j-1]);
}
else break;//提高效率
}
}
}
希爾排序
演算法思想
- 1, 確定一個起點a1,選取與其間距為id的元素構成一個子序列,L1={a1,a1+d,…a1+id},對其進行簡單插入排序,L1為有序
在確定新的起點a2,選取與其間距為id的元素構成一個子序列,L2={a2,a2+d,…a2+id},對其進行簡單插入排序,L2為有序
以次類推,最終得到d個子序列,且每個子序列均有序
因此,在L中間隔為d的元素已排好序
(在同一個子序列中的元素下標必構成公差為d的等差數列) - 2, 減小d,重複步驟1,直至d=1
例項講解
第一行為原始序列,d為增量
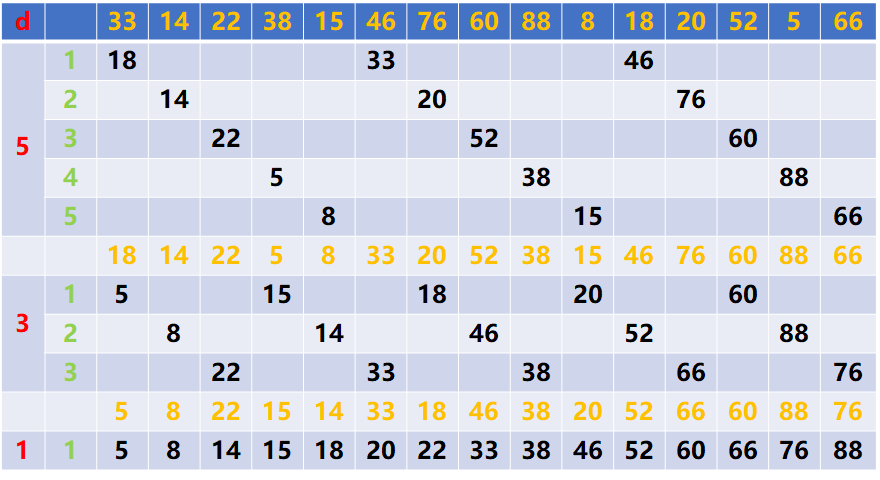
程式碼實現(C++)
tips:
- 1,每個序列的第一個預設是排好序的
- 2,一個序列分成dk個子序列時,
- 思路一:傳統是將i%dk相同的ai抽出來成為新序列,進而對該新序列使用簡單插入排序,再處理下一個序列
- 思路二:i%dk = {0,1,…dk-1} 在不同的子序列間來回處理,處理完餘數為0,立刻處理餘數為1,2,…dk-1。此思路為該程式的寫法
- 3,判斷條件中一發現當前數更大,立刻break,否則時間複雜度可能比簡單插入還高
- 4,這是測試快速排序時發現的問題:陣列下標越界,j>=dk,否則j-dk會溢位。很嚴重的問題是它溢位了照樣輸出,不終止,執行到快速排序就卡著了,誤導我以為是快排出現問題。
- 5,通過列印輸出找問題時又發現了一個嚴重問題:即使不通過應用L,陣列L.elem依舊被改變,原因在於雖然L作為形參傳入,但L.elem是指標,代表著地址,在函式中對其操作,相當於直接在其對應地址改動
- 6,要有自信,迅速定位問題位置,明白當前問題可能是由之前問題導致,連鎖反應,可見封裝的優越性。儘量不用遞迴,一是難調,二是耗空間
//=========================希爾排序============================
//希爾插入,按照一定的增量dk,進行插入排序
void ShellInsert(SqList L, int dk)
{
//=============思路一實現===========================
for(int k = 0; k < dk; k++)
{
for(int i = k + dk; i < L.length; i += dk)//i%dk = {0,1,...dk} 間來回轉換
{
// for(int j = i; j > 0; j -= dk)錯誤示例,會溢位
for(int j = i; j >= dk; j -= dk)
{
if(L.elem[j] < L.elem[j-dk])
{
swap(L.elem[j], L.elem[j-dk]);
}
else break;//不跳出時間複雜度比簡單插入還高
}
}
}
/*
//==================思路二實現=================
for(int i = 0 + dk; i < L.length; i ++)//i%dk = {0,1,...dk} 間來回轉換
{
for(int j = i; j >= dk; j -= dk)//方案一:控制j的範圍,j>=dk,否則會溢位
{
// if(j - dk >= 0)//方案二:注意判斷是否存在,否則j<dk時必溢位!!!!!!!!!
// {
if(L.elem[j] < L.elem[j-dk])//兩種解決方案
{
swap(L.elem[j], L.elem[j-dk]);
}
// }
else break;//不跳出時間複雜度比簡單插入還高
}
}*/
}
void ShellSort(SqList L)
{
int d[3] = {5,3,1};//增量數列
for(int i = 0; i < 3; i++)
{
ShellInsert(L,d[i]);
}
// TraverseSqList(L);
}
交換排序
簡單交換(冒泡)排序
演算法思想
兩兩比較,較大者往後走/較小者往前走
實現程式碼(C++)
//通過兩兩交換,求得最小值,從前往後填入
void BubbleSort(SqList L)
{
for(int i = 0; i < L.length - 1; i++)
{
for(int j = i+1; j < L.length; j++)
{
if(L.elem[i] > L.elem[j])
{
swap(L.elem[i],L.elem[j]);
}
}
}
// TraverseSqList(L);
}
快速排序
演算法思想
分割(核心):選取一個分割元素p,令p左邊元素均小於等於p,p右邊元素均大於等於p,因此,p的位置唯一確定。
因此,只需進行n次分割就可將長度為n的序列L排成有序序列
程式碼實現(C++)
遞迴版
//選擇一個值pivot作為軸對數列進行分割,左小右大,分割完成,pivot位置確定
//快速排序是對不斷對序列進行分割,每分一次,確定一個值的位置
int Partition(SqList L,int low,int high)
{
int i,j;//好習慣:儘量不改變引數
i = low;//頭
j = high;//尾
int t = L.elem[low];//儲存第一個,騰出空位
while(i < j)
{
while(i < j && t <= L.elem[j]) j--;//從j向前找到第一個比t小的值
L.elem[i] = L.elem[j];//填入空中 ,此時i的位置騰出
while(i < j && t >= L.elem[i]) i++;//從i向後找到第一個比t大的值
L.elem[j] = L.elem[i];//填入空中 ,此時j的位置騰出
}//跳出迴圈,i=j,且還必有一個空
L.elem[i] = t;//將開始的軸值填入最後一個空,該值位置確定,其左邊均比它小,右邊均比他大。
return i;//返回中軸的位置
}
//遞迴實現分割
void QSort(SqList L,int low,int high)
{
if(low < high)
{
int pivot = Partition(L,low,high);
QSort(L,low,pivot-1);
QSort(L,pivot+1,high);
}
}
//為了形式統一,介面一致,才寫了這個函式
void QuickSort(SqList L)
{
QSort(L,0,L.length - 1);
}
選擇排序
演算法思想
每趟選取一個最小值,往前放/每天選一個最大值,往後放
實現程式碼(C++)
//每趟選出一個最小值,從前往後放入第一個非有序位置
void SelectSort(SqList L)
{
for(int i = 0; i < L.length; i++)
{
int k = i;
for(int j = i + 1; j < L.length; j++)
{
if(L.elem[k] > L.elem[j]) k = j;//記錄最小值下標
}
if(k != i)//如果ai不是最小值 ,交換ak,ai,使ai成為最小值
{
swap(L.elem[k],L.elem[i]);
}
}
}
堆排序(大頂堆)
大頂堆是完全二叉樹,且任一子樹根均大於左右孩子
演算法思想
1,篩選(核心):堆排序關鍵是如何篩選出最大元素,可分為兩種情況
- 1,完全二叉樹除了根,左右子樹均已為大頂堆
- 2,除了情況1的情況
A,第一種情況(好辦)
- 1,令根a與其左右孩子中較大者a’比較,若a>=a’,無需再比;若a<a’,交換這兩個節點
- 2,重複1,直至a為葉子
B,第二種情況(轉化分解)
可以將情況二轉化為多個情況一,從而解決問題。
倒過來反覆使用解決方案A
- 1,完全二叉樹的葉子左右子樹均為大頂堆,所以可用A篩選
- 2,從最後向前一步步篩選,所以每個即將要篩選的節點的左右子樹均已為大頂堆,所以均可使用A篩選
2,建大頂堆
使用反覆篩選建立大頂堆,來一個元素,篩選一次。
3,排序
建好大頂堆後,將根元素與最後一個元素交換,同時完全二叉樹去除最後一個元素,再利用篩選,得到元素少一個的新大頂堆,重複直至僅有一個元素即可。
實現程式碼(C++)
//大頂堆--》升序;小頂堆-》降序
//篩選函式,使用前提:根的左右子樹都是堆,僅根破壞了大頂堆的定義
void HeapAdjust(SqList L,int low,int high)
{
int i,j;
i = low;
while(2*i <= high)//堆是完全二叉樹:左子堆存在
{
j = 2*i;//初值 ,每次需更新
if(2*i+1 <= high && L.elem[2*i] < L.elem[2*i+1]) j = 2*i+1;//若右子堆也存在,選擇左右大者
if(L.elem[i] < L.elem[j]) swap(L.elem[i],L.elem[j]);//若ai<aj,交換
else break;//否則立刻跳出,提升效率
i = j;//更新i
}
// TraverseSqList(L);
}
//亂序數列通過從最後一個開始向前反覆篩選可變為堆
//0號單元不用
void HSort(SqList L,int low,int high)
{
for(int i = high; i >= 1; i--)//整理成大頂堆
{
HeapAdjust(L,i,high);
}
// cout<<"12:";TraverseSqList(L);
int i,j;
i = low;
j = high;
//for(int k = 1; k < L.length; k++)//次數必須為n-1次,多一次少一次都不行 ???
while(true)
{//因為0號單元有元素,但是堆不用,0*x=0。所以排序次數多了會把0號元素捲入排序,導致錯誤
//方案一:嚴格控制次數:n-1次
//方案二:利用j=0跳出迴圈
if(j == 0)break;
swap(L.elem[i],L.elem[j]);
j--;
HeapAdjust(L,i,j);
}
}
//與快排相同,該函式僅是為了介面統一
void HeapSort(SqList L)
{
HSort(L,1,L.length-1);
}
歸併排序
兩個有序序列合併成一個有序序列
程式碼實現(C++)
- 遞迴與非遞迴合併演算法一致
- 遞迴簡潔,但效率一般不如非遞迴高,且不易除錯
合併兩條有序序列
//=========================歸併============================
void Merge(SqList &L1,int low,int m,int high)
{
int i,j,k=low;//錯誤示範:k=0。!!每次呼叫歸併起點並不都是0
i = low;
j = m+1;
SqList L2;
L2.length = L1.length;
L2.elem = (int*)malloc(N*sizeof(int));
while(i <= m && j <= high)//兩條序列均未走完
{
if(L1.elem[i] < L1.elem[j]) L2.elem[k++] = L1.elem[i++];
else L2.elem[k++] = L1.elem[j++];
}
//若是有一序列還未走完,直接將剩餘部分全部賦給新序列
while(i <= m) L2.elem[k++] = L1.elem[i++];
while(j <= high) L2.elem[k++] = L1.elem[j++];
for(int t = low; t <= high; t++)//low->high 才需賦值
{
L1.elem[t] = L2.elem[t];
}
free(L2.elem);
}
遞迴形式
//遞迴形式
void MSort(SqList L,int low,int high)
{
if(low >= high ) return;
int m = (low + high)/2;
MSort(L,low,m);
MSort(
