我們先來說個老生常談的情景：某天你去買芒果，小販攤了滿滿一車芒果，你一個個選好，拿給小販稱重，然後論斤付錢。

自然，你的目標是那些最甜最成熟的芒果，那怎麼選呢？你想起來，啊外婆說過，明黃色的比淡黃色的甜。你就設了條標準：只選明黃色的芒果。於是按顏色挑好、付錢、回家。啊哈，人生完整了？

呵呵呵。

告訴你吧人生就是各種麻煩

等你回到家，嚐了下芒果。有些確實挺甜，有些就不行了。額～顯然，外婆教的金科玉律還不夠用，光看顏色不靠譜哪。

閉關研究大半天以後，你得出結論：大個的明黃色芒果必然甜，小個的，就只有一半機率會是甜的了。

於是下次，你滿意地帶著這個結論再去買芒果，卻發現你經常光顧的那個小販關門度假去了。好吧，換家店，結果人家的進貨渠道還不一樣，那芒果是另一個地方種的。你這套法則不管用了，又得從頭再來。好吧，這家店裡每種芒果你都嚐了下，總結出來小個淡黃色的最甜。

還沒結束。你遠房表妹又來找你玩了。要招待些好的吧？但她說了，她無所謂芒果甜不甜，汁水多就行。好唄，你還得再做一次實驗，找到芒果越軟汁水越多的規律。

接著你又移民了。一嘗這邊的芒果，咦，新世界的大門打開了。綠色的芒果居然比黃色的好吃……

最後，你結婚了，領導表示不愛吃芒果，要吃蘋果。於是你所有關於芒果的知識都沒用了。只能按老方法再重新研究遍蘋果的物理特徵跟它味道好不好之間的關係。蘋果吃到吐？沒辦法，你愛老婆嘛。

有請碼農

好了，現在想象下，這一路辛酸曲折的，你寫了組程式幫忙減輕負擔。那程式邏輯基本應該類似這樣：

預設變數 顏色、大小、店家、硬度

如 顏色=明黃

大小=大

店家=經常光顧的小販

則 芒果=甜

如 硬度=軟

則 芒果=多汁

用著很爽吧，你甚至可以把這套玩意兒發給你小弟，他挑來的芒果也包你滿意。

但每做一次新實驗，你就得人肉改一次程式邏輯。而且你得首先保證自己已經理解了選芒果那套錯綜複雜的藝術，才能把它寫程序序裡。如果要求太複雜、芒果種類太多，那光把所有挑選規則翻譯成程式邏輯就夠你出一身大汗，相當於讀個“芒果學”博士了。

不是所有人都有“讀博”的功夫的。

有請“機器學習”演算法

機器學習演算法其實就是普通演算法的進化版。通過自動學習資料規律，讓你的程式變得更聰明些。

你從市場上隨機買一批芒果（訓練資料），把每隻芒果的物理屬性列一個表格出來，比如顏色、大小、形狀、產地、店家，等等（特徵

），對應芒果的甜度、汁水多少、成熟度，等等（輸出變數）。然後把這些資料扔給機器學習演算法（分類/迴歸），它就會自己計算出一個芒果物理屬性與其品質之間的相關性模型。

等下一次你去採購時，輸入店裡在賣的芒果的物理屬性（測試資料），機器學習演算法就會根據上次計算出來的模型來預測這些芒果品質如何。機器用的演算法可能跟你人肉寫的邏輯規則類似（比如決策樹），也有可能更先進，但反正基本上你不用多慮。

好啦，現在你可以信心滿滿去買芒果了，顏色大小啥的都是浮雲，交給機器去操心唄。更妙的是，你的演算法還會逐漸進化（強化學習）：根據其預測結果的正誤，演算法會自行修正模型，那麼隨著訓練資料的積累，到後來它的預測就會越來越準確。最妙的來了，用同一個演算法，你可以做好幾個模型，蘋果桔子香蕉葡萄各給爺來上一套，不要說老婆有令，就是七大姑八大嬸各有所好，也再不用發愁了。

用一句話總結機器學習就是：走自己的屌絲路，讓你的演算法牛逼去吧。

來源：Quora

機器學習常見演算法分類彙總（轉自：http://www.ctocio.com/hotnews/15919.html）

學習方式

根據資料型別的不同，對一個問題的建模有不同的方式。在機器學習或者人工智慧領域，人們首先會考慮演算法的學習方式。在機器學習領域，有幾種主要的學習方式。將演算法按照學習方式分類是一個不錯的想法，這樣可以讓人們在建模和演算法選擇的時候考慮能根據輸入資料來選擇最合適的演算法來獲得最好的結果。

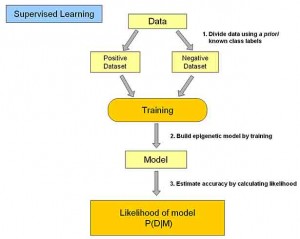
監督式學習：

在監督式學習下，輸入資料被稱為“訓練資料”，每組訓練資料有一個明確的標識或結果，如對防垃圾郵件系統中“垃圾郵件”“非垃圾郵件”，對手寫數字識別中的“1“，”2“，”3“，”4“等。在建立預測模型的時候，監督式學習建立一個學習過程，將預測結果與“訓練資料”的實際結果進行比較，不斷的調整預測模型，直到模型的預測結果達到一個預期的準確率。監督式學習的常見應用場景如分類問題和迴歸問題。常見演算法有邏輯迴歸（Logistic Regression）和反向傳遞神經網路（Back Propagation Neural Network）

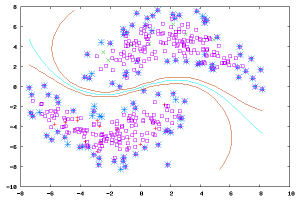
非監督式學習：

在非監督式學習中，資料並不被特別標識，學習模型是為了推斷出資料的一些內在結構。常見的應用場景包括關聯規則的學習以及聚類等。常見演算法包括Apriori演算法以及k-Means演算法。

半監督式學習：

在此學習方式下，輸入資料部分被標識，部分沒有被標識，這種學習模型可以用來進行預測，但是模型首先需要學習資料的內在結構以便合理的組織資料來進行預測。應用場景包括分類和迴歸，演算法包括一些對常用監督式學習演算法的延伸，這些演算法首先試圖對未標識資料進行建模，在此基礎上再對標識的資料進行預測。如圖論推理演算法（Graph Inference）或者拉普拉斯支援向量機（Laplacian SVM.）等。

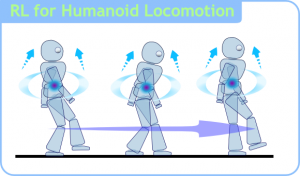
強化學習：

在這種學習模式下，輸入資料作為對模型的反饋，不像監督模型那樣，輸入資料僅僅是作為一個檢查模型對錯的方式，在強化學習下，輸入資料直接反饋到模型，模型必須對此立刻作出調整。常見的應用場景包括動態系統以及機器人控制等。常見演算法包括Q-Learning以及時間差學習（Temporal difference learning）

在企業資料應用的場景下， 人們最常用的可能就是監督式學習和非監督式學習的模型。 在影象識別等領域，由於存在大量的非標識的資料和少量的可標識資料， 目前半監督式學習是一個很熱的話題。 而強化學習更多的應用在機器人控制及其他需要進行系統控制的領域。

演算法類似性

根據演算法的功能和形式的類似性，我們可以把演算法分類，比如說基於樹的演算法，基於神經網路的演算法等等。當然，機器學習的範圍非常龐大，有些演算法很難明確歸類到某一類。而對於有些分類來說，同一分類的演算法可以針對不同型別的問題。這裡，我們儘量把常用的演算法按照最容易理解的方式進行分類。

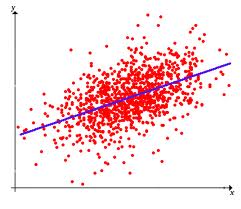
迴歸演算法：

迴歸演算法是試圖採用對誤差的衡量來探索變數之間的關係的一類演算法。迴歸演算法是統計機器學習的利器。在機器學習領域，人們說起迴歸，有時候是指一類問題，有時候是指一類演算法，這一點常常會使初學者有所困惑。常見的迴歸演算法包括：最小二乘法（Ordinary Least Square），邏輯迴歸（Logistic Regression），逐步式迴歸（Stepwise Regression），多元自適應迴歸樣條（Multivariate Adaptive Regression Splines）以及本地散點平滑估計（Locally Estimated Scatterplot Smoothing）

基於例項的演算法

 

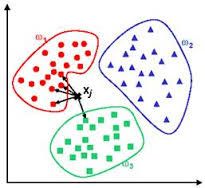
基於例項的演算法常常用來對決策問題建立模型，這樣的模型常常先選取一批樣本資料，然後根據某些近似性把新資料與樣本資料進行比較。通過這種方式來尋找最佳的匹配。因此，基於例項的演算法常常也被稱為“贏家通吃”學習或者“基於記憶的學習”。常見的演算法包括 k-Nearest Neighbor(KNN), 學習向量量化（Learning Vector Quantization， LVQ），以及自組織對映演算法（Self-Organizing Map ， SOM）

正則化方法

 

正則化方法是其他演算法（通常是迴歸演算法）的延伸，根據演算法的複雜度對演算法進行調整。正則化方法通常對簡單模型予以獎勵而對複雜演算法予以懲罰。常見的演算法包括：Ridge Regression， Least Absolute Shrinkage and Selection Operator（LASSO），以及彈性網路（Elastic Net）。

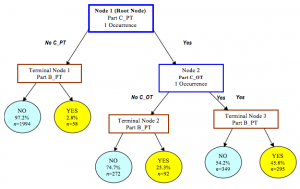
決策樹學習

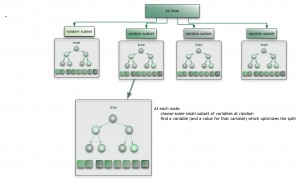
決策樹演算法根據資料的屬性採用樹狀結構建立決策模型， 決策樹模型常常用來解決分類和迴歸問題。常見的演算法包括：分類及迴歸樹（Classification And Regression Tree， CART）， ID3 (Iterative Dichotomiser 3)， C4.5， Chi-squared Automatic Interaction Detection(CHAID), Decision Stump, 隨機森林（Random Forest）， 多元自適應迴歸樣條（MARS）以及梯度推進機（Gradient Boosting Machine， GBM）

貝葉斯方法

貝葉斯方法演算法是基於貝葉斯定理的一類演算法，主要用來解決分類和迴歸問題。常見演算法包括：樸素貝葉斯演算法，平均單依賴估計（Averaged One-Dependence Estimators， AODE），以及Bayesian Belief Network（BBN）。

基於核的演算法

 

基於核的演算法中最著名的莫過於支援向量機（SVM）了。 基於核的演算法把輸入資料對映到一個高階的向量空間， 在這些高階向量空間裡， 有些分類或者回歸問題能夠更容易的解決。 常見的基於核的演算法包括：支援向量機（Support Vector Machine， SVM）， 徑向基函式（Radial Basis Function ，RBF)， 以及線性判別分析（Linear Discriminate Analysis ，LDA)等

聚類演算法

 

聚類，就像迴歸一樣，有時候人們描述的是一類問題，有時候描述的是一類演算法。聚類演算法通常按照中心點或者分層的方式對輸入資料進行歸併。所以的聚類演算法都試圖找到資料的內在結構，以便按照最大的共同點將資料進行歸類。常見的聚類演算法包括 k-Means演算法以及期望最大化演算法（Expectation Maximization， EM）。

關聯規則學習

 

關聯規則學習通過尋找最能夠解釋資料變數之間關係的規則，來找出大量多元資料集中有用的關聯規則。常見演算法包括 Apriori演算法和Eclat演算法等。

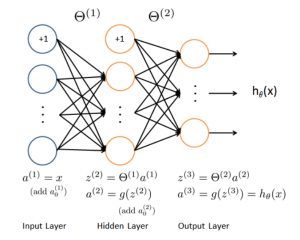
人工神經網路

 

人工神經網路演算法模擬生物神經網路，是一類模式匹配演算法。通常用於解決分類和迴歸問題。人工神經網路是機器學習的一個龐大的分支，有幾百種不同的演算法。（其中深度學習就是其中的一類演算法，我們會單獨討論），重要的人工神經網路演算法包括：感知器神經網路（Perceptron Neural Network）, 反向傳遞（Back Propagation）， Hopfield網路，自組織對映（Self-Organizing Map, SOM）。學習向量量化（Learning Vector Quantization， LVQ）

深度學習

 

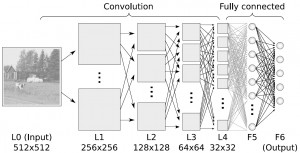
深度學習演算法是對人工神經網路的發展。 在近期贏得了很多關注， 特別是百度也開始發力深度學習後， 更是在國內引起了很多關注。   在計算能力變得日益廉價的今天，深度學習試圖建立大得多也複雜得多的神經網路。很多深度學習的演算法是半監督式學習演算法，用來處理存在少量未標識資料的大資料集。常見的深度學習演算法包括：受限波爾茲曼機（Restricted Boltzmann Machine， RBN）， Deep Belief Networks（DBN），卷積網路（Convolutional Network）, 堆疊式自動編碼器（Stacked Auto-encoders）。

降低維度演算法

 

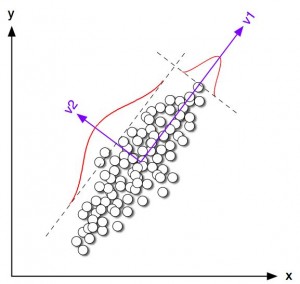
像聚類演算法一樣，降低維度演算法試圖分析資料的內在結構，不過降低維度演算法是以非監督學習的方式試圖利用較少的資訊來歸納或者解釋資料。這類演算法可以用於高維資料的視覺化或者用來簡化資料以便監督式學習使用。常見的演算法包括：主成份分析（Principle Component Analysis， PCA），偏最小二乘迴歸（Partial Least Square Regression，PLS）， Sammon對映，多維尺度（Multi-Dimensional Scaling, MDS）,  投影追蹤（Projection Pursuit）等。

整合演算法：

整合演算法用一些相對較弱的學習模型獨立地就同樣的樣本進行訓練，然後把結果整合起來進行整體預測。整合演算法的主要難點在於究竟整合哪些獨立的較弱的學習模型以及如何把學習結果整合起來。這是一類非常強大的演算法，同時也非常流行。常見的演算法包括：Boosting， Bootstrapped Aggregation（Bagging）， AdaBoost，堆疊泛化（Stacked Generalization， Blending），梯度推進機（Gradient Boosting Machine, GBM），隨機森林（Random Forest）。

常見機器學習演算法優缺點：

樸素貝葉斯：

　　有以下幾個地方需要注意：

　　1. 如果給出的特徵向量長度可能不同，這是需要歸一化為通長度的向量（這裡以文字分類為例），比如說是句子單詞的話，則長度為整個詞彙量的長度，對應位置是該單詞出現的次數。

　　2. 計算公式如下：

 　　

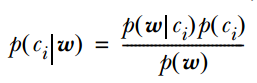
　　其中一項條件概率可以通過樸素貝葉斯條件獨立展開。要注意一點就是 的計算方法，而由樸素貝葉斯的前提假設可知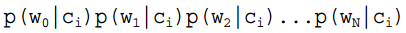， = ，因此一般有兩種，一種是在類別為ci的那些樣本集中，找到wj出現次數的總和，然後除以該樣本的總和；第二種方法是類別為ci的那些樣本集中，找到wj出現次數的總和，然後除以該樣本中所有特徵出現次數的總和。

　　3. 如果 中的某一項為0，則其聯合概率的乘積也可能為0，即2中公式的分子為0，為了避免這種現象出現，一般情況下會將這一項初始化為1，當然為了保證概率相等，分母應對應初始化為2（這裡因為是2類，所以加2，如果是k類就需要加k，術語上叫做laplace光滑, 分母加k的原因是使之滿足全概率公式）。

　　樸素貝葉斯的優點：

　　對小規模的資料表現很好，適合多分類任務，適合增量式訓練。

　　缺點：

　　對輸入資料的表達形式很敏感。

　　決策樹：

　　決策樹中很重要的一點就是選擇一個屬性進行分枝，因此要注意一下資訊增益的計算公式，並深入理解它。

　　資訊熵的計算公式如下:

 　　

　　其中的n代表有n個分類類別（比如假設是2類問題，那麼n=2）。分別計算這2類樣本在總樣本中出現的概率p1和p2，這樣就可以計算出未選中屬性分枝前的資訊熵。

　　現在選中一個屬性xi用來進行分枝，此時分枝規則是：如果xi=vx的話，將樣本分到樹的一個分支；如果不相等則進入另一個分支。很顯然，分支中的樣本很有可能包括2個類別，分別計算這2個分支的熵H1和H2,計算出分枝後的總資訊熵H’=p1*H1+p2*H2.，則此時的資訊增益ΔH=H-H’。以資訊增益為原則，把所有的屬性都測試一邊，選擇一個使增益最大的屬性作為本次分枝屬性。

　　決策樹的優點：

　　計算量簡單，可解釋性強，比較適合處理有缺失屬性值的樣本，能夠處理不相關的特徵；

　　缺點：

　　容易過擬合（後續出現了隨機森林，減小了過擬合現象）；

　　Logistic迴歸：

　　Logistic是用來分類的，是一種線性分類器，需要注意的地方有：

　　1. logistic函式表示式為：

 　　

　　其導數形式為：

 　　

　　2. logsitc迴歸方法主要是用最大似然估計來學習的，所以單個樣本的後驗概率為：

 　　

　　到整個樣本的後驗概率：

 　　

　　其中：

 　　

　　通過對數進一步化簡為：

 　　

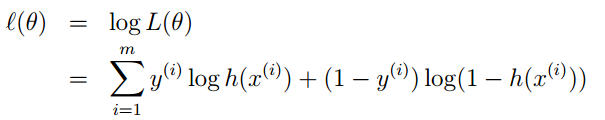
　　3. 其實它的loss function為-l(θ)，因此我們需使loss function最小，可採用梯度下降法得到。梯度下降法公式為:

 　　

　　

　　Logistic迴歸優點：

　　1、實現簡單；

　　2、分類時計算量非常小，速度很快，儲存資源低；

　　缺點：

　　1、容易欠擬合，一般準確度不太高

　　2、只能處理兩分類問題（在此基礎上衍生出來的softmax可以用於多分類），且必須線性可分；

　　線性迴歸：

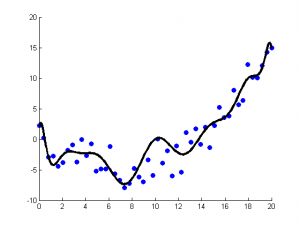
　　線性迴歸才是真正用於迴歸的，而不像logistic迴歸是用於分類，其基本思想是用梯度下降法對最小二乘法形式的誤差函式進行優化，當然也可以用normal equation直接求得引數的解，結果為：

 　　

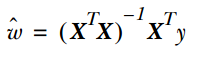
　　而在LWLR（區域性加權線性迴歸）中，引數的計算表示式為:

 　　

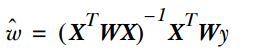
　　因為此時優化的是：

 　　

　　由此可見LWLR與LR不同，LWLR是一個非引數模型，因為每次進行迴歸計算都要遍歷訓練樣本至少一次。

　　線性迴歸優點：

　　實現簡單，計算簡單；

　　缺點：

　　不能擬合非線性資料；

　　KNN演算法：

　　KNN即最近鄰演算法，其主要過程為：

　　1. 計算訓練樣本和測試樣本中每個樣本點的距離（常見的距離度量有歐式距離，馬氏距離等）；

　　2. 對上面所有的距離值進行排序；

　　3. 選前k個最小距離的樣本；

　　4. 根據這k個樣本的標籤進行投票，得到最後的分類類別；

　　如何選擇一個最佳的K值，這取決於資料。一般情況下，在分類時較大的K值能夠減小噪聲的影響。但會使類別之間的界限變得模糊。一個較好的K值可通過各種啟發式技術來獲取，比如，交叉驗證。另外噪聲和非相關性特徵向量的存在會使K近鄰演算法的準確性減小。

　　近鄰演算法具有較強的一致性結果。隨著資料趨於無限，演算法保證錯誤率不會超過貝葉斯演算法錯誤率的兩倍。對於一些好的K值，K近鄰保證錯誤率不會超過貝葉斯理論誤差率。

　　注：馬氏距離一定要先給出樣本集的統計性質，比如均值向量，協方差矩陣等。關於馬氏距離的介紹如下：

 　　

　　KNN演算法的優點：

　　1. 思想簡單，理論成熟，既可以用來做分類也可以用來做迴歸；

　　2. 可用於非線性分類；

　　3. 訓練時間複雜度為O(n)；

　　4. 準確度高，對資料沒有假設，對outlier不敏感；

　　缺點：

　　1. 計算量大；

　　2. 樣本不平衡問題（即有些類別的樣本數量很多，而其它樣本的數量很少）；

　　3. 需要大量的記憶體；

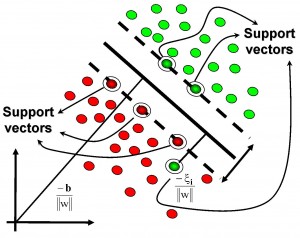
　　SVM：

　　要學會如何使用libsvm以及一些引數的調節經驗，另外需要理清楚svm演算法的一些思路：

　　1. svm中的最優分類面是對所有樣本的幾何裕量最大（為什麼要選擇最大間隔分類器，請從數學角度上說明？網易深度學習崗位面試過程中有被問到。答案就是幾何間隔與樣本的誤分次數間存在關係： ，其中的分母就是樣本到分類間隔距離，分子中的R是所有樣本中的最長向量值），即：

 　　

　　經過一系列推導可得為優化下面原始目標：

　　

　　2. 下面來看看拉格朗日理論：

　　

　　可以將1中的優化目標轉換為拉格朗日的形式（通過各種對偶優化，KKD條件），最後目標函式為：

 　　

　　我們只需要最小化上述目標函式，其中的α為原始優化問題中的不等式約束拉格朗日系數。

　　3. 對2中最後的式子分別w和b求導可得：

　　

　　 

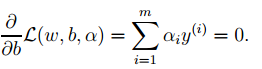
　　由上面第1式子可以知道，如果我們優化出了α，則直接可以求出w了，即模型的引數搞定。而上面第2個式子可以作為後續優化的一個約束條件。

　　4. 對2中最後一個目標函式用對偶優化理論可以轉換為優化下面的目標函式：

　　

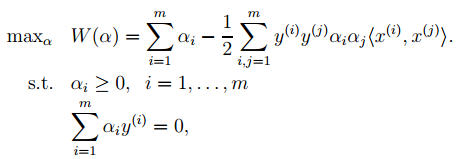
　　而這個函式可以用常用的優化方法求得α，進而求得w和b。

　　5. 按照道理，svm簡單理論應該到此結束。不過還是要補充一點，即在預測時有：

 　　

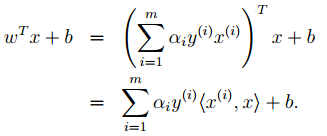
　　那個尖括號我們可以用核函式代替，這也是svm經常和核函式扯在一起的原因。

　　6. 最後是關於鬆弛變數的引入，因此原始的目標優化公式為：

 　　

　　此時對應的對偶優化公式為：

 　　

　　與前面的相比只是α多了個上界。

　　SVM演算法優點：

　　可用於線性/非線性分類，也可以用於迴歸；

　　低泛化誤差；

　　容易解釋；

　　計算複雜度較低；

　　缺點：

　　對引數和核函式的選擇比較敏感；

　　原始的SVM只比較擅長處理二分類問題；

　　Boosting：

　　主要以Adaboost為例，首先來看看Adaboost的流程圖，如下：

 　　

　　從圖中可以看到，在訓練過程中我們需要訓練出多個弱分類器（圖中為3個），每個弱分類器是由不同權重的樣本（圖中為5個訓練樣本）訓練得到（其中第一個弱分類器對應輸入樣本的權值是一樣的），而每個弱分類器對最終分類結果的作用也不同，是通過加權平均輸出的，權值見上圖中三角形裡面的數值。那麼這些弱分類器和其對應的權值是怎樣訓練出來的呢？

　　下面通過一個例子來簡單說明。

　　書中（machine learning in action）假設的是5個訓練樣本，每個訓練樣本的維度為2，在訓練第一個分類器時5個樣本的權重各為0.2. 注意這裡樣本的權值和最終訓練的弱分類器組對應的權值α是不同的，樣本的權重只在訓練過程中用到，而α在訓練過程和測試過程都有用到。

　　現在假設弱分類器是帶一個節點的簡單決策樹，該決策樹會選擇2個屬性（假設只有2個屬性）的一個，然後計算出這個屬性中的最佳值用來分類。

　　Adaboost的簡單版本訓練過程如下：

　　1. 訓練第一個分類器，樣本的權值D為相同的均值。通過一個弱分類器，得到這5個樣本（請對應書中的例子來看，依舊是machine learning in action）的分類預測標籤。與給出的樣本真實標籤對比，就可能出現誤差(即錯誤)。如果某個樣本預測錯誤，則它對應的錯誤值為該樣本的權重，如果分類正確，則錯誤值為0. 最後累加5個樣本的錯誤率之和，記為ε。

　　2. 通過ε來計算該弱分類器的權重α，公式如下：

 　　

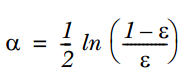
　　3. 通過α來計算訓練下一個弱分類器樣本的權重D，如果對應樣本分類正確，則減小該樣本的權重，公式為：

 　　

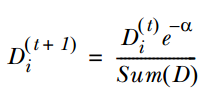
　　如果樣本分類錯誤，則增加該樣本的權重，公式為：

 　　

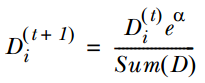
　　4. 迴圈步驟1,2,3來繼續訓練多個分類器，只是其D值不同而已。

　　測試過程如下：

　　輸入一個樣本到訓練好的每個弱分類中，則每個弱分類都對應一個輸出標籤，然後該標籤乘以對應的α，最後求和得到值的符號即為預測標籤值。

　　Boosting演算法的優點：

　　低泛化誤差；

　　容易實現，分類準確率較高，沒有太多引數可以調；

　　缺點：

　　對outlier比較敏感；

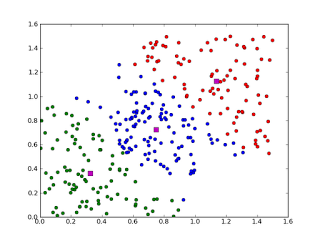
　　聚類：

　　根據聚類思想劃分：

　　1. 基於劃分的聚類:

　　K-means, k-medoids(每一個類別中找一個樣本點來代表),CLARANS.

　　k-means是使下面的表示式值最小：

 　　

　　 k-means演算法的優點：

　　（1）k-means演算法是解決聚類問題的一種經典演算法，演算法簡單、快速。

　　（2）對處理大資料集，該演算法是相對可伸縮的和高效率的，因為它的複雜度大約是O(nkt)，其中n是所有物件的數目，k是簇的數目,t是迭代的次數。通常k<<n。這個演算法通常區域性收斂。

　　（3）演算法嘗試找出使平方誤差函式值最小的k個劃分。當簇是密集的、球狀或團狀的，且簇與簇之間區別明顯時，聚類效果較好。

　　 缺點：

　　（1）k-平均方法只有在簇的平均值被定義的情況下才能使用，且對有些分類屬性的資料不適合。

　　（2）要求使用者必須事先給出要生成的簇的數目k。

　　（3）對初值敏感，對於不同的初始值，可能會導致不同的聚類結果。

　　（4）不適合於發現非凸面形狀的簇，或者大小差別很大的簇。

　　（5）對於"噪聲"和孤立點資料敏感，少量的該類資料能夠對平均值產生極大影響。

　　2. 基於層次的聚類：

　　自底向上的凝聚方法，比如AGNES。

　　自上向下的分裂方法，比如DIANA。

　　3. 基於密度的聚類：

　　DBSACN,OPTICS,BIRCH(CF-Tree),CURE.

　　4. 基於網格的方法：

　　STING, WaveCluster.

　　5. 基於模型的聚類：

　　EM,SOM,COBWEB.

　  推薦系統：

　　推薦系統的實現主要分為兩個方面：基於內容的實現和協同濾波的實現。

　　基於內容的實現：

　　不同人對不同電影的評分這個例子，可以看做是一個普通的迴歸問題，因此每部電影都需要提前提取出一個特徵向量(即x值)，然後針對每個使用者建模，即每個使用者打的分值作為y值，利用這些已有的分值y和電影特徵值x就可以訓練迴歸模型了(最常見的就是線性迴歸)。這樣就可以預測那些使用者沒有評分的電影的分數。（值得注意的是需對每個使用者都建立他自己的迴歸模型）

　　從另一個角度來看，也可以是先給定每個使用者對某種電影的喜好程度（即權值），然後學出每部電影的特徵，最後採用迴歸來預測那些沒有被評分的電影。

　　當然還可以是同時優化得到每個使用者對不同型別電影的熱愛程度以及每部電影的特徵。具體可以參考Ng在coursera上的ml教程：https://www.coursera.org/course/ml

　　基於協同濾波的實現：

　　協同濾波（CF）可以看做是一個分類問題，也可以看做是矩陣分解問題。協同濾波主要是基於每個人自己的喜好都類似這一特徵，它不依賴於個人的基本資訊。比如剛剛那個電影評分的例子中，預測那些沒有被評分的電影的分數只依賴於已經打分的那些分數，並不需要去學習那些電影的特徵。

　　SVD將矩陣分解為三個矩陣的乘積，公式如下所示：

 　　

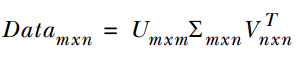
　　中間的矩陣sigma為對角矩陣，對角元素的值為Data矩陣的奇異值(注意奇異值和特徵值是不同的)，且已經從大到小排列好了。即使去掉特徵值小的那些特徵，依然可以很好的重構出原始矩陣。如下圖所示：

　　

　　其中更深的顏色代表去掉小特徵值重構時的三個矩陣。

　　果m代表商品的個數，n代表使用者的個數，則U矩陣的每一行代表商品的屬性，現在通過降維U矩陣（取深色部分）後，每一個商品的屬性可以用更低的維度表示（假設為k維）。這樣當新來一個使用者的商品推薦向量X，則可以根據公式X'*U1*inv(S1)得到一個k維的向量，然後在V’中尋找最相似的那一個使用者（相似度測量可用餘弦公式等），根據這個使用者的評分來推薦（主要是推薦新使用者未打分的那些商品）。具體例子可以參考網頁：SVD在推薦系統中的應用。

　　另外關於SVD分解後每個矩陣的實際含義可以參考google吳軍的《數學之美》一書（不過個人感覺吳軍解釋UV兩個矩陣時好像弄反了，不知道大家怎樣認為）。或者參考machine learning in action其中的svd章節。

　　pLSA:

　　pLSA由LSA發展過來，而早期LSA的實現主要是通過SVD分解。pLSA的模型圖如下：

 　　

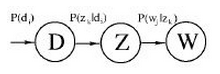
　　公式中的意義如下：

 　　

　　LDA：

　　主題模型，概率圖如下：

 　　

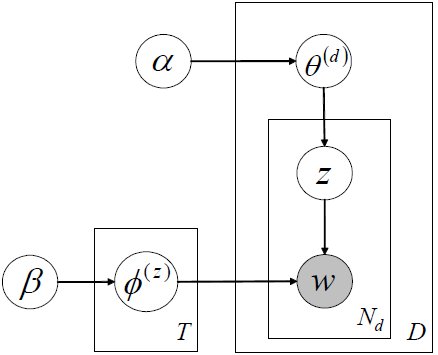
　　和pLSA不同的是LDA中假設了很多先驗分佈，且一般引數的先驗分佈都假設為Dirichlet分佈，其原因是共軛分佈時先驗概率和後驗概率的形式相同。

　　GDBT：

　　GBDT(Gradient Boosting Decision Tree) 又叫 MART（Multiple Additive Regression Tree)，好像在阿里內部用得比較多（所以阿里演算法崗位面試時可能會問到），它是一種迭代的決策樹演算法，該演算法由多棵決策樹組成，所有樹的輸出結果累加起來就是最終答案。它在被提出之初就和SVM一起被認為是泛化能力（generalization)較強的演算法。近些年更因為被用於搜尋排序的機器學習模型而引起大家關注。

　　GBDT是迴歸樹，不是分類樹。其核心就在於，每一棵樹是從之前所有樹的殘差中來學習的。為了防止過擬合，和Adaboosting一樣，也加入了boosting這一項。

　　Regularization:

　　作用是（網易電話面試時有問到）：

　　1. 數值上更容易求解；

　　2. 特徵數目太大時更穩定；

　　3. 控制模型的複雜度，光滑性。複雜性越小且越光滑的目標函式泛化能力越強。而加入規則項能使目標函式複雜度減小，且更光滑。

　　4. 減小引數空間；引數空間越小，複雜度越低。

　　5. 係數越小，模型越簡單，而模型越簡單則泛化能力越強（Ng巨集觀上給出的解釋）。

　　6. 可以看成是權值的高斯先驗。

　　異常檢測：

　　可以估計樣本的密度函式，對於新樣本直接計算其密度，如果密度值小於某一閾值，則表示該樣本異常。而密度函式一般採用多維的高斯分佈。如果樣本有n維，則每一維的特徵都可以看作是符合高斯分佈的，即使這些特徵可視化出來不太符合高斯分佈，也可以對該特徵進行數學轉換讓其看起來像高斯分佈，比如說x=log(x+c), x=x^(1/c)等。異常檢測的演算法流程如下：

 　　

 　　其中的ε也是通過交叉驗證得到的，也就是說在進行異常檢測時，前面的p(x)的學習是用的無監督，後面的引數ε學習是用的有監督。那麼為什麼不全部使用普通有監督的方法來學習呢（即把它看做是一個普通的二分類問題）？主要是因為在異常檢測中，異常的樣本數量非常少而正常樣本數量非常多，因此不足以學習到好的異常行為模型的引數，因為後面新來的異常樣本可能完全是與訓練樣本中的模式不同。

　　另外，上面是將特徵的每一維看成是相互獨立的高斯分佈，其實這樣的近似並不是最好的，但是它的計算量較小，因此也常被使用。更好的方法應該是將特徵擬合成多維高斯分佈，這時有特徵之間的相關性，但隨之計算量會變複雜，且樣本的協方差矩陣還可能出現不可逆的情況（主要在樣本數比特徵數小，或者樣本特徵維數之間有線性關係時）。

　　EM演算法：

　　有時候因為樣本的產生和隱含變數有關（隱含變數是不能觀察的），而求模型的引數時一般採用最大似然估計，由於含有了隱含變數，所以對似然函式引數求導是求不出來的，這時可以採用EM演算法來求模型的引數的（對應模型引數個數可能有多個），EM演算法一般分為2步：

　　E步：選取一組引數，求出在該引數下隱含變數的條件概率值；

　　M步：結合E步求出的隱含變數條件概率，求出似然函式下界函式（本質上是某個期望函式）的最大值。

　　重複上面2步直至收斂。

　　公式如下所示：

 　　

　　M步公式中下界函式的推導過程：

 　　

　　EM演算法一個常見的例子就是GMM模型，每個樣本都有可能由k個高斯產生，只不過由每個高斯產生的概率不同而已，因此每個樣本都有對應的高斯分佈（k箇中的某一個），此時的隱含變數就是每個樣本對應的某個高斯分佈。

　　GMM的E步公式如下（計算每個樣本對應每個高斯的概率）：

 　　

　　更具體的計算公式為：

　　

　　M步公式如下（計算每個高斯的比重，均值，方差這3個引數）：

 　　

　　Apriori:

　　Apriori是關聯分析中比較早的一種方法，主要用來挖掘那些頻繁項集合。其思想是：

　　1. 如果一個專案集合不是頻繁集合，那麼任何包含它的專案集合也一定不是頻繁集合；

　　2. 如果一個專案集合是頻繁集合，那麼它的任何非空子集也是頻繁集合；

　　Aprioir需要掃描專案表多遍，從一個專案開始掃描，捨去掉那些不是頻繁的專案，得到的集合稱為L，然後對L中的每個元素進行自組合，生成比上次掃描多一個專案的集合，該集合稱為C，接著又掃描去掉那些非頻繁的專案，重複…

　　看下面這個例子：

　　元素專案表格：

 　　

　　如果每個步驟不去掉非頻繁專案集，則其掃描過程的樹形結構如下：

 　　

　　在其中某個過程中，可能出現非頻繁的專案集，將其去掉（用陰影表示）為：

 　　

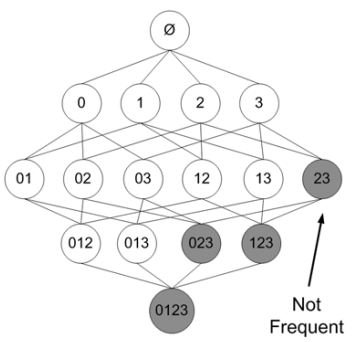
　　上面的內容主要參考的是machine learning in action這本書。

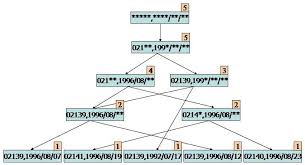
　　FP Growth:

　　FP Growth是一種比Apriori更高效的頻繁項挖掘方法，它只需要掃描專案表2次。其中第1次掃描獲得當個專案的頻率，去掉不符合支援度要求的項，並對剩下的項排序。第2遍掃描是建立一顆FP-Tree(frequent-patten tree)。

　　接下來的工作就是在FP-Tree上進行挖掘。

　　比如說有下表：

 　　

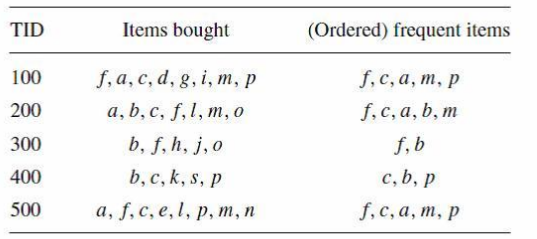
　　它所對應的FP_Tree如下：

 　　

　　然後從頻率最小的單項P開始，找出P的條件模式基，用構造FP_Tree同樣的方法來構造P的條件模式基的FP_Tree，在這棵樹上找出包含P的頻繁項集。

　　依次從m,b,a,c,f的條件模式基上挖掘頻繁項集，有些項需要遞迴的去挖掘，比較麻煩，比如m節點，具體的過程可以參考部落格：Frequent Pattern 挖掘之二(FP Growth演算法)，裡面講得很詳細。

轉自：http://www.cnblogs.com/tornadomeet