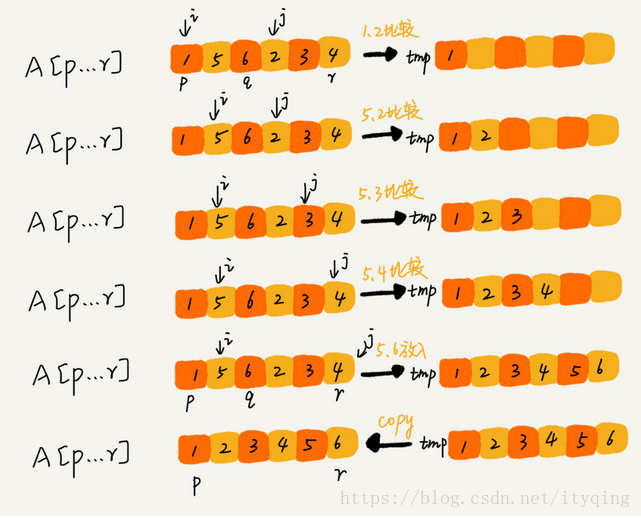資料結構與演算法學習筆記——排序
排序方法與複雜度歸類
(1)幾種最經典、最常用的排序方法:氣泡排序、插入排序、選擇排序、快速排序、歸併排序、計數排序、基數排序、桶排序。
(2)複雜度歸類
氣泡排序、插入排序、選擇排序 O(n^2)
快速排序、歸併排序 O(nlogn)
計數排序、基數排序、桶排序 O(n)
如何分析一個“排序演算法”
<1>演算法的執行效率
1. 最好、最壞、平均情況時間複雜度。
2. 時間複雜度的係數、常數和低階。
3. 比較次數,交換(或移動)次數。
<2>排序演算法的穩定性
1. 穩定性概念:如果待排序的序列中存在值相等的元素,經過排序之後,相等元素之間原有的先後順序不變。
2. 穩定性重要性:可針對物件的多種屬性進行有優先順序的排序。
3. 舉例:給電商交易系統中的“訂單”排序,按照金額大小對訂單資料排序,對於相同金額的訂單以下單時間早晚排序。用穩定排序演算法可簡潔地解決。先按照下單時間給訂單排序,排序完成後用穩定排序演算法按照訂單金額重新排序。
<3>排序演算法的記憶體損耗
原地排序演算法:特指空間複雜度是O(1)的排序演算法。
常見的排序演算法
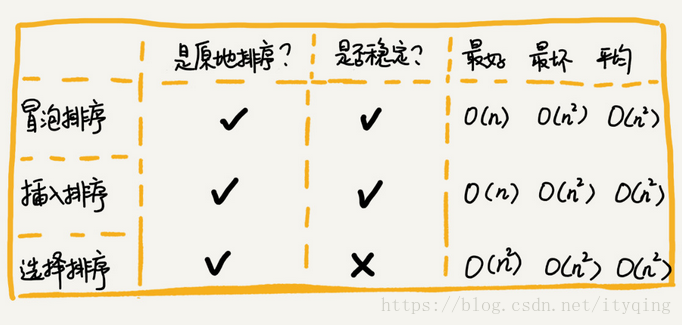
氣泡排序
氣泡排序只會操作相鄰的兩個資料。每次冒泡操作都會對相鄰的兩個元素進行比較,看是否滿足大小關係要求,如果不滿足就讓它倆互換。
程式碼:
public int[] bubbleSort(int[] a) { int n = a.length; if (n<=1) return a; //提前退出冒泡迴圈的標誌 boolean flag = false; for (int i = 0; i < n; i++) { for (int j = 0; j < n-i-1; j++) { if (a[j]>a[j+1]) {// int temp = a[j]; a[j] = a[j+1]; a[j+1] = temp; flag = true;//表示有資料交換 } } if (!flag) break; //沒有資料交換(說明已排好序無需再進行冒泡),提前退出 } return a; }
插入排序
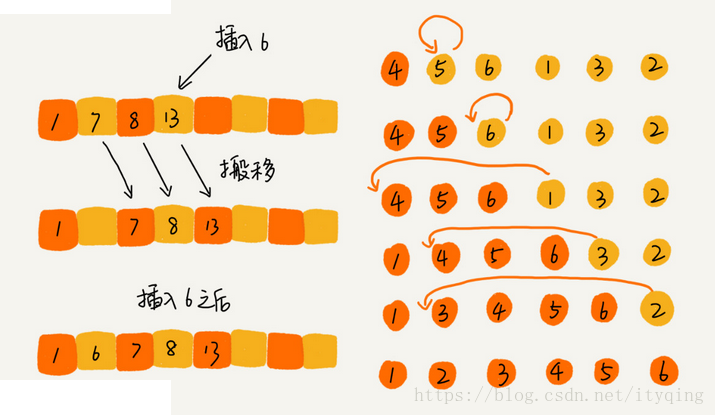
插入排序將陣列資料分成已排序區間和未排序區間。初始已排序區間只有一個元素,即陣列第一個元素。在未排序區間取出一個元素插入到已排序區間的合適位置,直到未排序區間為空。
程式碼:
public int[] insertionSort(int[] a) { int n = a.length; if (n<=1) return a; for (int i = 1; i < n; i++) { int value = a[i]; int j = i-1; for (; j >=0; j--) { if (a[j] > value) { a[j+1] = a[j];//移動資料 }else { break; } } a[j+1] = value;//插入資料 } return a; }
選擇排序
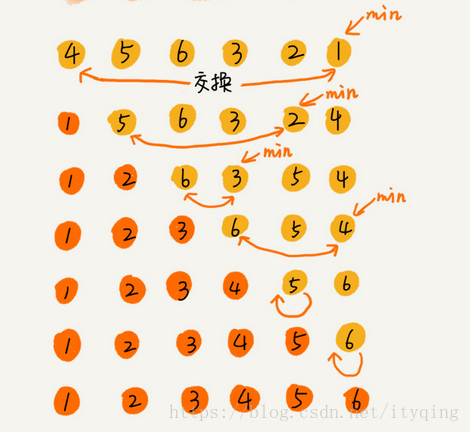
選擇排序將陣列分成已排序區間和未排序區間。初始已排序區間為空。每次從未排序區間中選出最小的元素插入已排序區間的末尾,直到未排序區間為空。
程式碼:
public int[] selectionSort(int[] a) {
int n = a.length;
for (int i = 0; i < a.length - 1; i++) {
for (int j = i+1; j < a.length; j++) {
//交換
if (a[i] > a[j]) {
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
return a;
}歸併排序
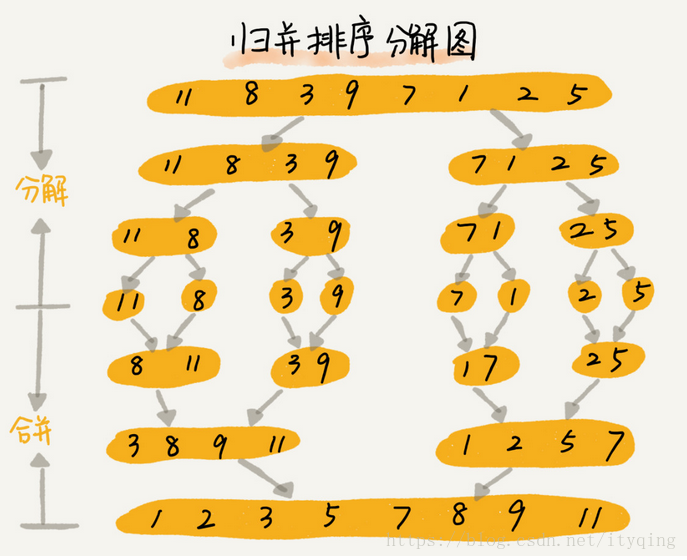
如果要排序一個數組,我們先把陣列從中間分成前後兩部分,然後對前後兩部分分別排序,再將排好序的兩部分合並在一起,這樣整個陣列就都有序了。
實現思路:
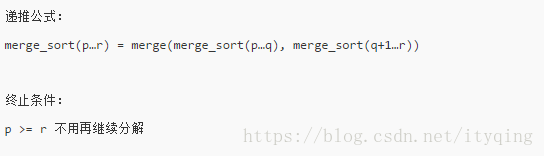
merge-sort(p...r)表示,給下標從p到r之間的陣列排序。我們將這個排序問題轉化為了兩個子問 ,題, merge_sort(p...q)和merge-sort(q+1..r),其中下標q等於p和r的中間位置,也就是, (p+r)/2,當下標從p到q和從q+1到r這兩個子陣列都排好序之後,我們再將兩個有序的子數組合並在一起,這樣下標從p到r之間的資料就也排好序了。
程式碼:
// 歸併排序演算法, a是陣列,n表示陣列大小
public static void mergeSort(int[] a, int n) {
mergeSortInternally(a, 0, n-1);
}
// 遞迴呼叫函式
private static void mergeSortInternally(int[] a, int p, int r) {
// 遞迴終止條件
if (p >= r) return;
// 取p到r之間的中間位置q
int q = (p+r)/2;
// 分治遞迴
mergeSortInternally(a, p, q);
mergeSortInternally(a, q+1, r);
// 將A[p...q]和A[q+1...r]合併為A[p...r]
merge(a, p, q, r);
}
private static void merge(int[] a, int p, int q, int r) {
int i = p;
int j = q+1;
int k = 0; // 初始化變數i, j, k
int[] tmp = new int[r-p+1]; // 申請一個大小跟a[p...r]一樣的臨時陣列
// 1 排序
while (i<=q && j<=r) {
if (a[i] <= a[j]) {
tmp[k++] = a[i++]; // i++等於i:=i+1
} else {
tmp[k++] = a[j++];
}
}
// 2 判斷哪個子陣列中有剩餘的資料
int start = i;
int end = q;
if (j <= r) {
start = j;
end = r;
}
// 3 將剩餘的資料拷貝到臨時陣列tmp
while (start <= end) {
tmp[k++] = a[start++];
}
// 4 將tmp中的陣列拷貝回a[p...r]
for (i = 0; i <= r-p; ++i) {
a[p+i] = tmp[i];
}
}
merge是這樣執行的:
程式碼分析:
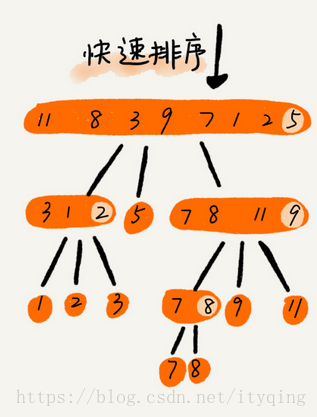
快速排序
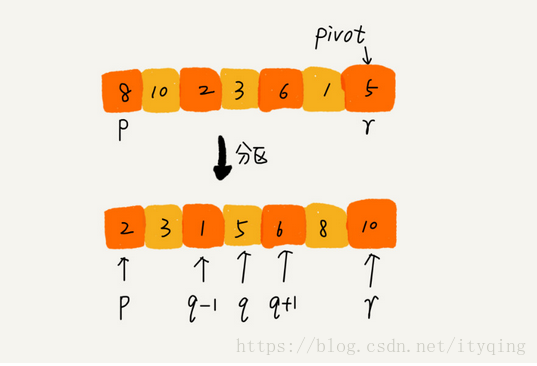
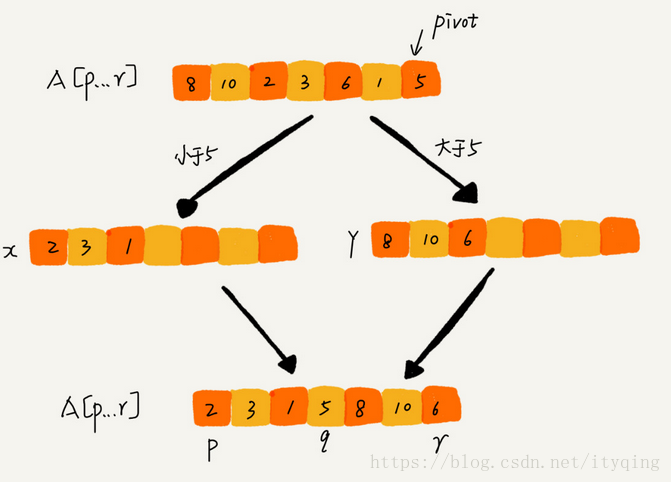
快排的思想: 如果要排序陣列中下標從p到r之間的一組資料,我們選擇p到r之間的任意一個數據作為pivot (分割槽點) 。-我們遍歷p到r之間的資料,將小於pivot的放到左邊,將大於pivot的放到右邊,將pivot放到中間。經過這一步驟之後,陣列p到r之間的資料就被分成了三個部分,前面p到q-1之間都是小於pivot的,中間是pivot,後面的q+1到r之間是大於pivot的。
快排利用的分而治之的思想
線性排序:
時間複雜度O(n)
我們把時間複雜度是線性的排序演算法叫作線性排序(Linear sort)常見的線性演算法有: 桶排序、計數排序、基數排序
特點:
非基於比較的排序演算法
桶排序
桶排序,顧名思義,會用到“桶" ,核心思想是將要排序的資料分到幾個有序的桶裡,每個桶裡的資料再單獨進行排序。桶內排完序之後,再把每個桶裡的資料按照順序依次取出,組成的序列就是有序的了。
對排序的資料要求苛刻:
1, 要排序的資料需要很容易就能劃分成m個桶,並且,桶與桶之間有著天然的大小順序。
2 ,資料在各個桶之間的分佈是比較均勻的。
3 ,桶排序比較適合用在外部排序中。所謂的外部排序就是資料儲存在外部磁碟中,資料量比較大,記憶體有限,無法將資料全部載入到記憶體中。
計數排序
計數排序只能用在資料範圍不大的場景中,如果資料範圍k比要排序的資料n大很多,就不適合用計數排序了。
計數排序只能給非負整數排序,如果要排序的資料是其他型別的,要將其在不改變相對大小的情況下,轉化為非負整數。
程式碼:
// 計數排序,a是陣列,n是陣列大小。假設陣列中儲存的都是非負整數。
public static void countingSort(int[] a) {
int n = a.length;
if (n <= 1) return;
// 查詢陣列中資料的範圍
int max = a[0];
for (int i = 1; i < n; ++i) {
if (max < a[i]) {
max = a[i];
}
}
// 申請一個計數陣列c,下標大小[0,max]
int[] c = new int[max + 1];
for (int i = 0; i < max + 1; ++i) {
c[i] = 0;
}
// 計算每個元素的個數,放入c中
for (int i = 0; i < n; ++i) {
c[a[i]]++;
}
// 依次累加
for (int i = 1; i < max + 1; ++i) {
c[i] = c[i-1] + c[i];
}
// 臨時陣列r,儲存排序之後的結果
int[] r = new int[n];
// 計算排序的關鍵步驟了,有點難理解
for (int i = n - 1; i >= 0; --i) {
int index = c[a[i]]-1;
r[index] = a[i];
c[a[i]]--;
}
// 將結果拷貝會a陣列
for (int i = 0; i < n; ++i) {
a[i] = r[i];
}
}