***好記性不如爛筆頭*** 轉自： https://www.cnblogs.com/yssongest/p/5303151.html

1，原理
　　在影象的仿射變換中，很多地方需要用到插值運算，常見的插值運算包括最鄰近插值，雙線性插值，雙三次插值，蘭索思插值等方法，OpenCV提供了很多方法，其中，雙線性插值由於折中的插值效果和運算速度，運用比較廣泛。
　　越是簡單的模型越適合用來舉例子，我們就舉個簡單的影象：3*3 的256級灰度圖。假如影象的象素矩陣如下圖所示（這個原始圖把它叫做源圖，Source）：
       234 38 22
       67 44 12
       89 65 63
　　這 個矩陣中，元素座標(x,y)是這樣確定的，x從左到右，從0開始，y從上到下，也是從零開始，這是圖象處理中最常用的座標系。
　　如果想把這副圖放大為 4*4大小的影象，那麼該怎麼做呢？那麼第一步肯定想到的是先把4*4的矩陣先畫出來再說，好了矩陣畫出來了，如下所示，當然，矩陣的每個畫素都是未知數，等待著我們去填充（這個將要被填充的圖的叫做目標圖,Destination）：
　　? ? ? ?
　　? ? ? ?
　　? ? ? ?
　　? ? ? ? 
　　然後要往這個空的矩陣裡面填值了，要填的值從哪裡來來呢？是從源圖中來，好，先填寫目標圖最左上角的象素，座標為（0，0），那麼該座標對應源圖中的座標可以由如下公式得出srcX=dstX* (srcWidth/dstWidth) , srcY = dstY * (srcHeight/dstHeight)
　　好了，套用公式，就可以找到對應的原圖的座標了(0*(3/4),0*(3/4))=>(0*0.75,0*0.75)=>(0,0)，找到了源圖的對應座標,就可以把源圖中座標為(0,0)處的234象素值填進去目標圖的(0,0)這個位置了。
　　接下來,如法炮製,尋找目標圖中座標為(1,0)的象素對應源圖中的座標,套用公式:
(1*0.75,0*0.75)=>(0.75,0) 結果發現,得到的座標裡面竟然有小數,這可怎麼辦?計算機裡的影象可是數字影象,象素就是最小單位了,象素的座標都是整數,從來沒有小數座標。這時候採用的一種策略就是採用四捨五入的方法（也可以採用直接舍掉小數位的方法），把非整數座標轉換成整數，好，那麼按照四捨五入的方法就得到座標（1，0），完整的運算過程就是這樣的：(1*0.75,0*0.75)=>(0.75,0)=>(1,0) 那麼就可以再填一個象素到目標矩陣中了，同樣是把源圖中座標為(1,0)處的畫素值38填入目標圖中的座標。
　　依次填完每個象素，一幅放大後的影象就誕生了，畫素矩陣如下所示：
　　234 38 22 22 
　　67 44 12 12 
　　89 65 63 63 
　　89 65 63 63 
　　這種放大影象的方法叫做最臨近插值演算法，這是一種最基本、最簡單的影象縮放演算法，效果也是最不好的，放大後的影象有很嚴重的馬賽克，縮小後的影象有很嚴重的失真；效果不好的根源就是其簡單的最臨近插值方法引入了嚴重的影象失真，比如，當由目標圖的座標反推得到的源圖的的座標是一個浮點數的時候，採用了四捨五入的方法，直接採用了和這個浮點數最接近的象素的值，這種方法是很不科學的，當推得座標值為 0.75的時候，不應該就簡單的取為1，既然是0.75，比1要小0.25 ，比0要大0.75 ,那麼目標象素值其實應該根據這個源圖中虛擬的點四周的四個真實的點來按照一定的規律計算出來的，這樣才能達到更好的縮放效果。
　　雙線型內插值演算法就是一種比較好的影象縮放演算法，它充分的利用了源圖中虛擬點四周的四個真實存在的畫素值來共同決定目標圖中的一個畫素值，因此縮放效果比簡單的最鄰近插值要好很多。
雙線性內插值演算法描述如下:
　　對於一個目的畫素，設定座標通過反向變換得到的浮點座標為(i+u,j+v) (其中i、j均為浮點座標的整數部分，u、v為浮點座標的小數部分，是取值[0,1)區間的浮點數)，則這個畫素得值 f(i+u,j+v) 可由原影象中座標為 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所對應的周圍四個畫素的值決定，即：f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1) 
其中f(i,j)表示源影象(i,j)處的的畫素值，以此類推。
　　比如，象剛才的例子，現在假如目標圖的象素座標為（1，1），那麼反推得到的對應於源圖的座標是（0.75 , 0.75）, 這其實只是一個概念上的虛擬象素,實際在源圖中並不存在這樣一個象素,那麼目標圖的象素（1，1）的取值不能夠由這個虛擬象素來決定，而只能由源圖的這四個象素共同決定：（0，0）（0，1）（1，0）（1，1），而由於（0.75,0.75）離（1，1）要更近一些，那麼（1,1）所起的決定作用更大一些，這從公式1中的係數uv=0.75×0.75就可以體現出來，而（0.75,0.75）離（0，0）最遠，所以（0，0）所起的決定作用就要小一些，公式中係數為(1-u)(1-v)=0.25×0.25也體現出了這一特點。
2，計算方法

　　首先，在X方向上進行兩次線性插值計算，然後在Y方向上進行一次插值計算。
　　

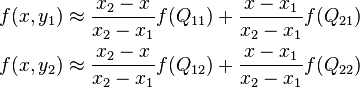
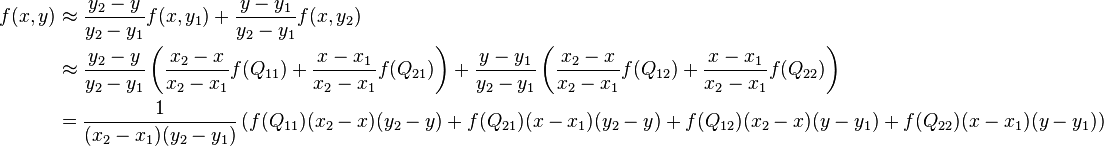
　　在影象處理的時候，我們先根據
　　srcX=dstX* (srcWidth/dstWidth) ,
　　srcY = dstY * (srcHeight/dstHeight)
來計算目標畫素在源影象中的位置，這裡計算的srcX和srcY一般都是浮點數，比如f（1.2, 3.4）這個畫素點是虛擬存在的，先找到與它臨近的四個實際存在的畫素點
　　（1，3） （2，3）
　　（1，4） （2，4）
　　寫成f(i+u,j+v)的形式，則u=0.2,v=0.4, i=1, j=3
　　在沿著X方向差插值時，f(R1)=u(f(Q21)-f(Q11))+f(Q11)
　　沿著Y方向同理計算。
　　或者，直接整理一步計算，f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1) 。
3，加速以及優化策略

• 源影象和目標影象幾何中心的對齊。
• 將浮點運算轉換成整數運算

3.1 源影象和目標影象幾何中心的對齊　　

　　方法：在計算源影象的虛擬浮點座標的時候，一般情況：
　　srcX=dstX* (srcWidth/dstWidth) ,
　　srcY = dstY * (srcHeight/dstHeight)
　　中心對齊(OpenCV也是如此)：
　　SrcX=(dstX+0.5)* (srcWidth/dstWidth) -0.5

      雙線性插值演算法及需要注意事項這篇部落格解釋說“如果選擇右上角為原點（0，0），那麼最右邊和最下邊的畫素實際上並沒有參與計算，而且目標影象的每個畫素點計算出的灰度值也相對於源影象偏左偏上。”我有點保持疑問。
　　將公式變形，srcX=dstX* (srcWidth/dstWidth)+0.5*(srcWidth/dstWidth-1)
　　相當於我們在原始的浮點座標上加上了0.5*(srcWidth/dstWidth-1)這樣一個控制因子，這項的符號可正可負，與srcWidth/dstWidth的比值也就是當前插值是擴大還是縮小影象有關，有什麼作用呢？看一個例子：假設源影象是3*3，中心點座標（1，1）目標影象是9*9，中心點座標（4，4），我們在進行插值對映的時候，儘可能希望均勻的用到源影象的畫素資訊，最直觀的就是（4,4）對映到（1,1）現在直接計算srcX=4*3/9=1.3333！=1，也就是我們在插值的時候所利用的畫素集中在影象的右下方，而不是均勻分佈整個影象。現在考慮中心點對齊，srcX=(4+0.5)*3/9-0.5=1，剛好滿足我們的要求。
3.2 將浮點運算轉換成整數運算
　　參考影象處理界雙線性插值演算法的優化
　　直接進行計算的話，由於計算的srcX和srcY 都是浮點數，後續會進行大量的乘法，而影象資料量又大，速度不會理想，解決思路是：浮點運算→→整數運算→→”<<左右移按位運算”。
　　放大的主要物件是u，v這些浮點數，OpenCV選擇的放大倍數是2048“如何取這個合適的放大倍數呢，要從三個方面考慮，第一：精度問題，如果這個數取得過小，那麼經過計算後可能會導致結果出現較大的誤差。第二，這個數不能太大，太大會導致計算過程超過長整形所能表達的範圍。第三：速度考慮。假如放大倍數取為12，那麼算式在最後的結果中應該需要除以12*12=144，但是如果取為16，則最後的除數為16*16=256，這個數字好，我們可以用右移來實現，而右移要比普通的整除快多了。”我們利用左移11位操作就可以達到放大目的。
4，程式碼

uchar* dataDst = matDst1.data;
    int stepDst = matDst1.step;
    uchar* dataSrc = matSrc.data;
    int stepSrc = matSrc.step;
    int iWidthSrc = matSrc.cols;
    int iHiehgtSrc = matSrc.rows;

    for (int j = 0; j < matDst1.rows; ++j)
    {
        float fy = (float)((j + 0.5) * scale_y - 0.5);
        int sy = cvFloor(fy);
        fy -= sy;
        sy = std::min(sy, iHiehgtSrc - 2);
        sy = std::max(0, sy);

        short cbufy[2];
        cbufy[0] = cv::saturate_cast<short>((1.f - fy) * 2048);
        cbufy[1] = 2048 - cbufy[0];

        for (int i = 0; i < matDst1.cols; ++i)
        {
            float fx = (float)((i + 0.5) * scale_x - 0.5);
            int sx = cvFloor(fx);
            fx -= sx;

            if (sx < 0) {
                fx = 0, sx = 0;
            }
            if (sx >= iWidthSrc - 1) {
                fx = 0, sx = iWidthSrc - 2;
            }

            short cbufx[2];
            cbufx[0] = cv::saturate_cast<short>((1.f - fx) * 2048);
            cbufx[1] = 2048 - cbufx[0];

            for (int k = 0; k < matSrc.channels(); ++k)
            {
                *(dataDst+ j*stepDst + 3*i + k) = (*(dataSrc + sy*stepSrc + 3*sx + k) * cbufx[0] * cbufy[0] + 
                    *(dataSrc + (sy+1)*stepSrc + 3*sx + k) * cbufx[0] * cbufy[1] + 
                    *(dataSrc + sy*stepSrc + 3*(sx+1) + k) * cbufx[1] * cbufy[0] + 
                    *(dataSrc + (sy+1)*stepSrc + 3*(sx+1) + k) * cbufx[1] * cbufy[1]) >> 22;
            }
        }
    }
    cv::imwrite("linear_1.jpg", matDst1);

    cv::resize(matSrc, matDst2, matDst1.size(), 0, 0, 1);
    cv::imwrite("linear_2.jpg", matDst2);

參考：OpenCV中resize函式五種插值演算法的實現過程

         影象放縮中最近鄰插值和雙線性插值的基本原理