演算法和資料操作
• 遞迴和迴圈：
很多演算法可以用遞迴和迴圈兩種不同方式實現。
通常基於遞迴的實現方法程式碼會比較簡潔，但效能不如基於迴圈的實現方法。
• 排序和查詢：
重點掌握二分查詢，歸併排序和快速排序。
例 題11旋轉陣列的最小數字
• 回溯法：
要求在二維陣列（迷宮或棋盤）上搜索路徑用回溯法。
通常回溯法很適合用遞迴的程式碼實現。
如果限定不可以用遞迴，考慮用棧來模擬。
【題12矩陣中的路徑，13 機器人的運動範圍】
• 動態規劃：
求某個問題的最優解，並且該問題可以分為多個子問題。
用自上而下的遞迴思路去分析動態規劃問題的時候，會發現子問題之間存在重疊的更小的子問題。
為了避免重複計算，用自下而上的迴圈程式碼實現，把子問題的最優解先算出來並用陣列（一維或者二維）儲存下來，接下來基於子問題的解計算大問題的解。
• 貪婪演算法：

動態規劃的思路後，還在提醒在分解子問題的時候是不是存在某個特殊的選擇，如果採用這個特殊的選擇將一定能得到最優解，那麼採用貪婪演算法。
【題14 剪繩子】
• 位運算：
一類特殊的演算法，把數字表示成二進位制之後對0和1的操作。由於位運算的物件為二進位制數字，所以不是很直觀，
共有與，或，異或，左移和右移5種運算。
【題15 二進位制中1的個數】

遞迴和迴圈
遞迴是在一個函式的內部呼叫這個函式自身。
迴圈是通過設定計算的初始值和終止條件，在一個範圍內重複計算。
遞迴優點：簡潔
遞迴缺點：
（1）由於是函式呼叫自身，函式呼叫是由時間和空間消耗的。
（2）很多計算時重複的，對效能帶來負面影響。
（3）棧溢位：函式呼叫在棧中分配空間，而每個程序的棧的容量時有限的，當遞迴呼叫的層級太多時，就會超出棧的容量，導致棧溢位。
【題10 斐波那契數列】

【題目一】
寫一個函式，輸入n，求斐波那契（Fibonacci）數列的第n項，斐波那契數列的定義如下

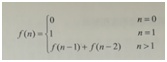
<效率很低的解法，不喜歡>

評價：
這種解法存在效率問題。這棵樹中有很多節點是重複的，而且重複的節點會隨著n的增大而急劇增加，這意味著計算量會隨著n的增大而急劇增大。用遞迴方法計算的時間複雜度是以n的指數的方式遞增的。

<期待的實用解法：避免重複計算>
從下往上計算
（1） 首先根據f(0)和f(1)計算出f(2),
（2） 再根據f(1)和f(2)計算f(3)
……
依次類推算出第n項了。時間複雜度為O(n)

<時間複雜度O(logn)，但不夠實用的解法>

數學公式：（可以用數學歸納法證明）

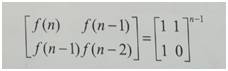
有了這個公式，只需求得矩陣

即得到f(n)
現在問題轉成如何求矩陣

的乘方。
考慮乘方的性質。

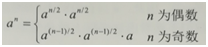
想求n次方，就要先求得n/2次方，再把n/2次方的結果平方一下即可。遞迴實現。

實現

package ti10;

/**
 * 劍指offer面試題9：斐波那契數列
 * 題目：寫一個函式，輸入n，求斐波那契數列的第n項。
 * 　　　　　　　　　　　　　　　　　　　　0,                n=1
 *     斐波那契數列定義如下：f(n)=      1,                n=2
 *                              　　 f(n-1)+f(n-2),    n>2

 */
public class No9Fibonacci {

    public static void main(String[] args) {
        System.out.println("第4項斐波那契數列的值為："+fibonacci(4));
    }

    /*
     * 採用遞迴實現斐波那契數列生成函式，效率低
     */
    public static int generateFibonacci(int n){
        if(n==0)
            return 0;
        if(n==1)
            return 1;
        return generateFibonacci(n-1)+generateFibonacci(n-2);
    }
    
    /*
     * 採用迴圈實現斐波那契數列
     * 儲存數列中間項，求得結果
     */
    public static int fibonacci(int n){
        int[] result={0,1};
        if(n<2)
            return result[n];
        int fibNMinusOne=1;
        int fibNMinusTwo=0;
        int fibN=0;
        for(int i=2;i<=n;i++){
            fibN=fibNMinusOne+fibNMinusTwo;
            fibNMinusTwo=fibNMinusOne;
            fibNMinusOne=fibN;
        }
        return fibN;
    }
}

解法比較：
法一：基於遞迴的解法：直觀，但時間效率很低。實際軟體開發中不會用這種方法。
法二：把遞迴演算法用迴圈實現：極大提高了時間效率。
法三：把求斐波那契數列轉換成求矩陣的乘方。可以用O(logn)求得矩陣的n次方，但由於隱含時間常數較大，很少有軟體採用這種方法。

【題目二：青蛙跳臺階問題】
一隻青蛙依次可以跳上1級臺階，也可以跳上2級臺階。求該青蛙跳上一個n級臺階總共有多少種跳法。
分析：
（1）考慮最簡單情況：
如果只有1級臺階，顯然一種 跳法
如果只有2級臺階，有兩種跳法1.分兩次跳，每次1級。 2．一次兩級
（2）一般情況：
把 n級臺階時跳法看成n的函式，記為f(n).
當n>2時，第一次跳的時候有兩種不同選擇：
1.第一次只跳1級，此時跳法數目等於後面剩下的n-1級臺階的跳法數目f(n-1)
2.第一次跳2級，此時跳法數目等於後面剩下的n-2級臺階跳法數目，即為f(n-2)
因此，n級臺階的不同跳法的總數為f(n)=f(n-1)+f(n-2)

實現

package ti10;

public class P77_FrogJumpFloor {
    public int FrogJumpFloor(int target) {
        int result = 0;
        if (target == 2 || target == 1) {
             result = target;
        }
        int temp1 = 1;
        int temp2 = 2;

        for (int i = 3; i <= target; i++) {
            result = temp1 + temp2;
            temp1 = temp2;
            temp2 = result;
        }
        return result;
    }
    public static void main(String[] args) {
        int n = 2;
        P77_FrogJumpFloor test = new P77_FrogJumpFloor();
        int result = test.FrogJumpFloor(n);
        System.out.print(result);
    }
}

【擴充套件】
在青蛙跳臺階問題中，如果把條件改成：一隻青蛙一次可以跳上1級臺階，也可以跳上2級……它也可以跳上n級，此時該青蛙跳上一個n級臺階總共有多少種跳法？
數學歸納法可以證明f(n)=2^(n-1)
分析
假設f(n)是n個臺階跳的次數。

1. f(1) = 1
2. f(2) 會有兩個跳得方式，一次1階或者2階，這回歸到了問題f(1),f(2) = f(2-1) + f(2-2)
3. f(3) 會有三種跳得方式，1階、2階、3階，那麼就是第一次跳出1階後面剩下：f(3-1);第一次跳出2階，剩下f(3-2)；第一次3階，那麼剩下f(3-3).因此結論是f(3) 會有三種跳得方式，1階、2階、3階，那麼就是第一次跳出1階後面剩下：f(3-1);第一次跳出2階，剩下f(3-2)；第一次3階，那麼剩下f(3-3).因此結論是
   f(3) = f(3-1)+f(3-2)+f(3-3)
4. f(n)時，會有n中跳的方式，1階、2階…n階
5. 得出結論：
   f(n) = f(n-1)+f(n-2)+…+f(n-(n-1)) + f(n-n)
   f(0) + f(1) + f(2) + f(3) + … + f(n-1) == f(n) = 2f(n-1)
   即f(n) = 2f(n-1)

每個臺階都有跳與不跳兩種情況（除了最後一個臺階），最後一個臺階必須跳。所以共用2^(n-1)中情況

實現

package ti10;

public class Solution {
    public int JumpFloorII(int target) {
        int result=0;
        if(target==0)
        {result=0;
        }else if(target==1)
        {result=1;
        }else{
            result=2*JumpFloorII(target-1);
        }
        
      return result; 
     
    }
    public static void main(String[] args) {
        int n = 5;
        Solution test = new Solution();
        int result = test.JumpFloorII(n);
        System.out.print(result);
    }

}

【相關題目】
我們可以用21（左圖）的小矩形橫著或者豎著去覆蓋更大的矩形，請問用8個21的小矩形無重疊地覆蓋一個2*8的大矩形（右圖）總共有多少種方法？

把2 * 8的覆蓋方法即為f(8)
第一個2 * 1的小矩形去覆蓋大矩形最左邊時有兩種選擇：豎著放，橫著放。
豎著放時，右邊剩下2 * 7區域，覆蓋方法記為f(7)
橫著放時，當小矩形橫著放在左上角時，左下角必須放一個，
右邊還剩2 * 6，覆蓋方法記為f(6)
因此f(8)=f(7)+f(6).

參考：
1.《劍指offer》
2.https://www.cnblogs.com/gl-developer/p/6445445.html
3.https://blog.csdn.net/Sunshine_liang1/article/details/82468306
4.https://blog.csdn.net/xiaomei920528/article/details/74178927