皮爾森相關係數Pearson correlation coefficient
今天老闆突然推薦瞭解下皮爾森相關係數,有些莫名其妙,看了下,就是之前在數理統計裡學到的相關係數,還是比較容易理解的,不過還是寫點記錄下學到的東西吧。
皮爾森相關係數(Pearson correlation coefficient)也稱皮爾森積矩相關係數(Pearson product-moment correlation coefficient) ,是一種線性相關係數,是最常用的一種相關係數。記為r,用來反映兩個變數X和Y的線性相關程度,r值介於-1到1之間,絕對值越大表明相關性越強。
定義:
總體相關係數ρ定義為兩個變數X、Y之間的協方差和標準差的比值,如下:
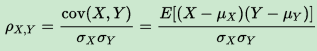
估算樣本的協方差和標準差,可得到樣本相關係數(即樣本皮爾森相關係數),常用r表示:
r還可以由(Xi,Yi)樣本點的標準分數均值估計得到與上式等價的表示式:
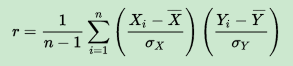
其中
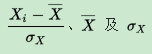 為Xi樣本的標準分數、樣本均值和樣本標準差,n為樣本數量。
為Xi樣本的標準分數、樣本均值和樣本標準差,n為樣本數量。
物理意義:
皮爾森相關係數反映了兩個變數的線性相關性的強弱程度,r的絕對值越大說明相關性越強。當r>0時,表明兩個變數正相關,即一個變數值越大則另一個變數值也會越大;當r<0時,表明兩個變數負相關,即一個變數值越大則另一個變數值反而會越小;當r=0時,表明兩個變數不是線性相關的(注意只是非線性相關),但是可能存在其他方式的相關性(比如曲線方式);當r=1和-1時,意味著兩個變數X和Y可以很好的由直線方程來描述,所有樣本點都很好的落在一條直線上。
皮爾森距離:
通過皮爾森係數定義:
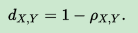
皮爾森係數範圍為[-1,1],因此皮爾森距離範圍為[0,2]。
相關推薦
皮爾森相關係數Pearson correlation coefficient
今天老闆突然推薦瞭解下皮爾森相關係數,有些莫名其妙,看了下,就是之前在數理統計裡學到的相關係數,還是比較容易理解的,不過還是寫點記錄下學到的東西吧。 皮爾森相關係數(Pearson correlation coefficient)也稱皮爾森積矩相關係數(P
Spearman秩相關係數和Pearson皮爾森相關係數
1、Pearson皮爾森相關係數 皮爾森相關係數也叫皮爾森積差相關係數,用來反映兩個變數之間相似程度的統計量。或者說用來表示兩個向量的相似度。 皮爾森相關係數計算公式如下: 分子是協方差,分母兩個向量的標準差的乘積。顯然是要求兩個向量的標準差不為零
皮爾森相關係數演算法
皮爾森相關係數(Pearson correlation coefficient)也稱皮爾森積矩相關係數(Pearson product-moment correlation coefficient) ,是一種線性相關係數。皮爾森相關係數是用來反映兩個變數線性相關程度的統計量。相關係數用r表示,其中n為樣本
[線性相關] 皮爾森相關係數的計算及假設檢驗
皮爾森相關係數,又稱積差相關係數、積矩相關係數,可以看做將兩組資料首先做Z分數處理之後, 然後兩組資料的乘積和除以樣本數Z分數一般代表正態分佈中, 資料偏離中心點的距離.等於變數減掉平均數再除以標準差。按照大學的線性數學水平來理解, 它比較複雜一點,可以看做是兩組資料的向量
相關性檢驗--Spearman秩相關係數和皮爾森相關係數
本文給出兩種相關係數,係數越大說明越相關。你可能會參考另一篇部落格獨立性檢驗。 皮爾森相關係數 皮爾森相關係數(Pearson correlation coefficient)也叫皮爾森積差相關係數(Pearson product-moment correlation coefficient),是用來反應兩
Pearson(皮爾遜)相關係數
統計相關係數簡介 由於使用的統計相關係數比較頻繁,所以這裡就利用幾篇文章簡單介紹一下這些係數。 相關係數:考察兩個事物(在資料裡我們稱之為變數)之間的相關程度。 如果有兩個變數:X、Y,最終計算出的相關係數的含義可以
皮爾遜相關係數和餘弦相似度
先看看二者定義,給定兩個n維向量A,B: A=(a1,a2,…,an)A = (a_1, a_2, \ldots ,a_n)A=(a1,a2,…,an) B=(b1,b2,…,bn)B = (b_1, b_2, \ldots ,b_n)B=(b1,b2
【126】TensorFlow 使用皮爾遜相關係數找出和標籤相關性最大的特徵值
在實際應用的時候,我們往往會收集多個維度的特徵值。然而這些特徵值未必都能派上用場。有些特徵值可能和標籤沒有什麼太大關係,而另外一些特徵值可能和標籤有很大的相關性。相關性不大的特徵值對於訓練模型沒有太大用處,還會影響效能。因此,最佳方式是找到相關性最大的幾個特
推薦演算法之-皮爾遜相關係數計算兩個使用者喜好相似度
<?php /** * 餘玄相似度計算出3個使用者的相似度 * 通過7件產品分析使用者喜好相似度 * 相似度使用函式 sim(user1,user2) =cos∂ * * 設A、B為多維
集體智慧程式設計-皮爾遜相關係數程式碼理解
剛開始看關於皮爾遜相關係數計算的程式碼,把我看得是暈頭轉向,不過在學習完概率論的課程後,發現結合公式再來看程式碼就會比較簡單了。 期望公式 E(x)=1n∑i=1nxi 方差公式 var(x)=
如何通俗易懂地理解皮爾遜相關係數?
要理解 Pearson 相關係數,首先要理解協方差(Covariance)。協方差表示兩個變數 X,Y 間相互關係的數字特徵,其計算公式為: COV(X,Y)=1n−1∑n1(Xi−X⎯⎯⎯)(Yi−Y⎯⎯⎯) 當 Y = X 時,即與方差相同。當變數 X,
資料探勘之曼哈頓距離、歐幾裡距離、明氏距離、皮爾遜相關係數、餘弦相似度Python實現程式碼
# -*- coding:utf8 -*- from math import sqrt users = {"Angelica": {"Blues Traveler": 3.5, "Broken Bells": 2.0, "Norah Jones": 4.5, "Phoeni
皮爾遜相關係數 定義+python程式碼實現 (與王印討論公式)
作者簡介 南京大學,簡稱南大,[1] 是一所源遠流長的高等學府。追溯學脈古為源自孫吳永安元年的南京太學,歷經多次變遷,1949年“國立中央大學”易名“國立南京大學”,翌年徑稱“南京大學”,沿用至今。南京大學是教育部與江蘇省共建的全國重點大學,國家首批“211工程”、“9
利用皮爾遜相關係數找出與目標最相關的特徵(Python實現)
#coding:utf-8 #檢測各特徵和輻照度之間的相關性以及各個特徵之間的相關性 from __future__ import division import tensorflow as tf import math import csv from sklearn imp
皮爾遜相關係數的計算(python程式碼版)
作者簡介 南京大學,簡稱南大,[1] 是一所源遠流長的高等學府。追溯學脈古為源自孫吳永安元年的南京太學,歷經多次變遷,1949年“國立中央大學”易名“國立南京大學”,翌年徑稱“南京大學”,沿用至今。南京大學是教育部與江蘇省共建的全國重點大學,國家首批“211工程”、“9
marchine learning 之 皮爾遜相關係數
/**皮爾遜相關係數 * ρ =(∑xy - ∑x∑y/n)/(∑x^2 - (∑x)^2/n)(∑y^2-(∑y)^2/n)^0.5 */ public class PersonCorrelati
①協方差、相關係數(皮爾遜相關係數),等同於:內積、餘弦值。
假設三維空間裡有很多點,每個點都是用三個維度來表示的。但你發現其實他們差不多都在同一個二維平面上。雖然不是完全在一個平面上,但距離那個平面的距離都很小,遠小於他們在這個平面上的互相距離。於是你想,如果把所有點都投影到這個二維平面,那你就可以用兩個維度來表示所有點,同時又不損失太多關於這些點的資訊。當你這麼做的
相似度演算法之皮爾遜相關係數
皮爾遜相關係數是比歐幾里德距離更加複雜的可以判斷人們興趣的相似度的一種方法。該相關係數是判斷兩組資料與某一直線擬合程式的一種試題。它在資料不是很規範的時候,會傾向於給出更好的結果。 如圖,Mick Lasalle為<<Superman>>評了3分
【機器學習】歐幾里德距離和皮爾遜相關係數(筆記)
歐幾里德距離() 歐幾里德距離和皮爾遜相關係數在機器學習中都是對相關度的計算,歐幾里德距離是以人們一直評價的物品作為座標軸,將參與評價的人繪製到圖中,並考察他們彼此距離的遠近。例子(摘自集體智慧程式設計): #資料集 critics={ 'Lisa Rose':
Spark/Scala實現推薦系統中的相似度演算法(歐幾里得距離、皮爾遜相關係數、餘弦相似度:附實現程式碼)
在推薦系統中,協同過濾演算法是應用較多的,具體又主要劃分為基於使用者和基於物品的協同過濾演算法,核心點就是基於"一個人"或"一件物品",根據這個人或物品所具有的屬性,比如對於人就是性別、年齡、工作、收入、喜好等,找出與這個人或物品相似的人或物,當然實際處理中參考的因子會複雜的多。 本篇文章不介紹相關數學概念,