演算法小結--快速排序+歸併排序
快速排序和歸併排序都是採用分治的思想,將一個無序序列不斷細分,然後慢慢組合成有序序列。
快速排序:它的基本思想是:根據基準通過一趟排序將要排序的資料分割成獨立的兩部分,其中一部分的所有資料都比另外一部分的所有資料都要小,然後再按此方法對這兩部分資料分別進行快速排序,整個排序過程可以遞迴進行,以此達到整個資料變成有序序列。
粗體為劃分基準 key=4
序號 1 2 3 4 5 6 7 8
輸入 4 2 8 7 1 3 5 6
從頭部開始找比key大的數,找到後停留i=3,再從尾部開始找比key小的數j=6,找到後交換兩個值,以此方式,知道i>=j 退出。
一次劃分:2 3 1 4
然後 將 2 3 1 和 7 8 5 6 按第一次的方式劃分
直至完成。
程式碼實現:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define n 5
//#define RAND_MAX
int a[n]={2,6,4,3,1};
void Swap(int i,int j)
{
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
int Partition(int p,int r)
{
int 快速排序一般情況都是以第一個元素作為key進行劃分,這樣容易出現太大的偶然性。如果key值差不多是這個有序序列的中間值,那麼排序效率比較高,如果不能將序列劃分成等同的兩塊,那麼效率會降低。
改進方法,在序列中隨機抽取key值,降低偶然性。
實現如下:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define n 5
//#define RAND_MAX
int a[n]={2,6,4,3,1};
void Swap(int i,int j)
{
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
int Partition(int p,int r)
{
int i = p,j=r+1;
int x = a[p];
while(1)
{
while(a[++i]<x&&i<r); //從左到右,直到找到比x大的,或者i<r
while(a[--j]>x); //從右到左,直到找到比x小的
if(i>=j) break;
Swap(i,j);
}
a[p] = a[j]; //將基準插入對應位置
a[j] = x;
return j;
}
int RandomPartition(int p,int r)
{
int t =(int) (p+(r-p)*rand()/RAND_MAX); //產生p到r的整數
Swap(t,p);
return Partition(p,r);
}
void QuickSort(int p,int r)
{
int q;
if(p<r)
{
//q = Partition(p,r);
q = RandomPartition(p,r); //啟用基準元素隨機化
QuickSort(p,q-1);
QuickSort(q+1,r);
}
}
int main()
{
int i;
QuickSort(0,n-1);
for(i=0;i<n;i++)
{
printf("%d ",a[i]);
}
return 0;
}
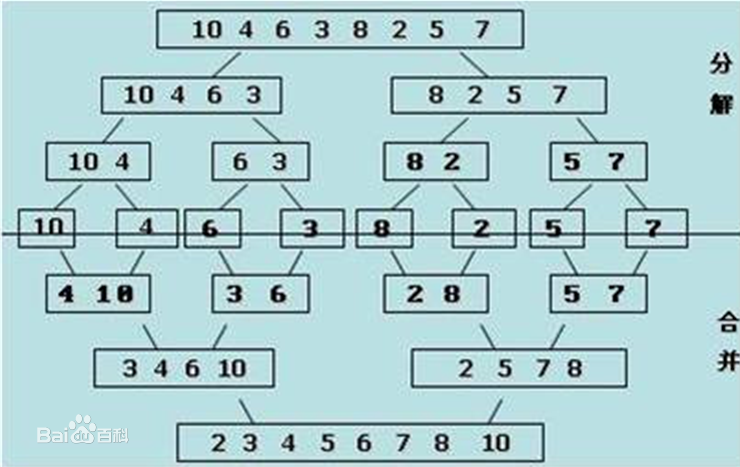
歸併排序:
合併排序法是將兩個(或兩個以上)有序表合併成一個新的有序表,即把待排序序列分為若干個子序列,每個子序列是有序的。然後再把有序子序列合併為整體有序序列。
程式碼如下:
#include <stdio.h>
#include <stdlib.h>
#define n 6
int a[n]={7,2,9,4,7,1};
int b[n]={0};
void Copy(int l,int r)
{
int i;
for(i=l;i<=r;i++)
{
a[i]=b[i];
}
}
void Merge(int l,int m,int r)
{
//合併c[l,m]和c[m+1,r] 到d[l,r]
int i =l,j = m+1,k = l;
while( (i<=m) && (j<=r))
{
if( a[i]<=a[j] ) b[k++]=a[i++];
else b[k++] = a[j++];
}
int q;
if(i>m)
{
for(q=j;q<=r;q++)
b[k++]=a[q];
}else
{
for(q=i;q<=m;q++)
b[k++]=a[q];
}
int s;
for(s=l;s<=r;s++)
{
//printf("%d \n",b[s]);
a[s]=b[s];
}
}
void MergeSort(int left,int right)
{
if(left < right)
{
int i = (left+right)/2;
MergeSort(left,i);
MergeSort(i+1,right);
Merge(left,i,right); //合併到陣列b
//Copy(left,right); //複製到陣列a
}
}
int main()
{
MergeSort(0,n-1);
int i;
for(i=0;i<n;i++)
{
printf("%d ",a[i]);
}
printf("\n");
return 0;
}
相關推薦
演算法小結--快速排序+歸併排序
快速排序和歸併排序都是採用分治的思想,將一個無序序列不斷細分,然後慢慢組合成有序序列。 快速排序:它的基本思想是:根據基準通過一趟排序將要排序的資料分割成獨立的兩部分,其中一部分的所有資料都比另外一部分的所有資料都要小,然後再按此方法對這兩部分資料分別進
經典排序演算法的實現(選擇,插入,shell,堆,快速,歸併排序)
1.選擇排序 //選擇排序 void selectSort(int * arr, int n) { for (int i = 0; i < n - 1; i++) { int min = arr[i]; int minPos = i; for (int j = i
常見比較排序演算法的實現(歸併排序、快速排序、堆排序、選擇排序、插入排序、希爾排序)
這篇部落格主要實現一些常見的排序演算法。例如: //氣泡排序 //選擇排序 //簡單插入排序 //折半插入排序 //希爾排序 //歸併排序 //雙向的快速排序(以及快速排序的非遞迴版本) //單向的快速排序 //堆排序 對於各個演算法的實現
常用演算法--基本排序演算法(氣泡排序,選擇排序,插入排序,快速排序,歸併排序,桶排序)
1.氣泡排序: 思想:以小到大排序為例,對無序的資料兩兩進行比較,大的放在右面,小的放在左面. (1,2),(1,3)...(2,3),(2,4)...(n-1,n-1),(n-1,n) 時間複雜度: O(n) ~ O(n2)O(n2~ Java程式碼實現: p
排序演算法: 氣泡排序, 快速排序,希爾排序,直接插入排序 ,直接選擇排序,歸併排序,堆排序
幾種排序演算法分析: 氣泡排序: 氣泡排序的方法排序速度比較慢。 思路:進行n-1排序,第一次排序先找出最小的數字,放在第一個位置,然後在剩餘的數字中再找出最小的數字,放在第二個位置上,依次類推,可以排出所有的數字。 當然也可以從大到小的排序。 例如
【C++實現】基本排序演算法 插入排序——歸併排序——快速排序——堆排序
/* 排序總結:(基於100w隨機數,有序數、重複數測試) 1、插入排序適合近乎有序的序列 2、歸併排序優化:(優化前 120S) 1)資料小於15時採用插入排序 10S 2)避免頻繁動態申請記憶體 memcpy(dest,src,sizeof(int)*len)
Java-時間複雜度為O(nlogn)的排序演算法(快速排序, 歸併排序, 堆排序, 希爾排序)
/** 包含多種靜態排序方法 * Created by Andre on 2016/6/27. */ public class Sorter { /** * 快速排序 * 遞迴形式 * 第一個記錄為樞軸 * 不穩定
其他排序演算法:快速、歸併、堆排序(top N)
快速排序 快速排序是一種分治排序演算法,採用了遞迴的方法。 原理: 1.先從數列中取出一個數作為基準數。 2.分割槽過程:將比這個數大的數全放到它的右邊,小於或等於它的數全放到它的左邊。 3.對左右區間重複第二步,直到各區間只有一個數
從零開始學演算法(四)歸併排序
從零開始學演算法(四)歸併排序 歸併排序 演算法介紹 演算法原理 演算法簡單記憶說明 演算法複雜度和穩定性 程式碼實現 歸併排序 程式碼是Javascript語言寫的(幾乎是虛擬碼) 演算
演算法第五記-歸併排序
今天我要講的排序演算法是歸併排序,首先我想提出一個問題(很多演算法題的思路都源於此),給定兩個已排序的序列,如何將其兩個序列合併為一個大序列並且依然保持有序。思路很簡單每個小序列維持一個指標指向左邊界,然後兩個序列的左邊界進行比較大小,小的那方加入新的序列中
單鏈表的排序(關鍵詞:連結串列/單鏈表/排序/快速排序/歸併排序)
https://leetcode.com/problems/sort-list/ https://leetcode.com/problems/sort-list/discuss/46807/Quick-sort-Merge-sort-Python https://leetcode.com
java排序演算法(四)------歸併排序
歸併排序: 是利用歸併的思想實現的排序方法,該演算法採用經典的分治(divide-and-conquer)策略(分治法將問題分(divide)成一些小的問題然後遞迴求解,而治(conquer)的階段則將分的階段得到的各答案"修補"在一起,即分而治之)。 合
演算法設計與分析——歸併排序
演算法思想 虛擬碼 MERGE-SORT A[1…n] 1.If n= 1, done. 2.Recursively sort A[ 1 . . .n/2.]and A[ [n/2]+1 . . n ] . 3.“Merge” the 2 sorted li
排序演算法c語言描述---歸併排序
排序算法系列學習,主要描述氣泡排序,選擇排序,直接插入排序,希爾排序,堆排序,歸併排序,快速排序等排序進行分析。文章規劃:一。通過自己對排序演算法本身的理解,對每個方法寫個小測試程式。 具體思路分析不展開描述。二。通過《大話資料結構》一書的截圖,詳細分析該演算法 。 在此,推薦
希爾、快速、歸併排序總結
冒泡、選擇、插入排序的效率都是O(N^2),但插入排序稍微快一些 歸併排序的效率是O(NlogN),希爾排序的效率大約是O(N(logN)2),快速排序需要O(N*logN)時間,希爾排序效率不穩定O(N*N(1.3~2)),理論上歸併比快速還要快,但歸併要建立
js演算法:分治法-歸併排序
歸併排序(合併排序)是一個遞迴演算法,這個演算法的理解其實可以藉助下面這個圖: 對於原始的陣列2,1,3,8,5,7,6,4,10,在整個過程執行的是順序是途中紅色編號1-20。雖然我們描述中說的是程式先分解,再歸併,但實際過程是一邊分解一邊歸併,前半部分分先排好序,後半
排序演算法:二路歸併排序(java)
public class MergeSort { /** * * @param array 待排序陣列 * @param temp 輔助陣列 * @param start 開始下標 * @param end 結束下標
Luogu 1177 - 【模板】快速排序 - [快速排序][歸併排序][無旋Treap]
題目連結:https://www.luogu.org/problemnew/show/P1177 題意:輸入 $n$ 以及後續 $n$ 個整數,讓你將這 $n$ 個整數從小到大排序輸出。 歸併排序(用時: 121ms / 記憶體: 1568KB): #inclu
五十道程式設計小題目 --- 28 八大排序演算法 java 之 07歸併排序
7. 歸併排序(Merge Sort) 基本思想: 歸併(Merge)排序法是將兩個(或兩個以上)有序表合併成一個新的有序表,即把待排序序列分為若干個子序列,每個子序列是有序的。然後再把有序子序列合併為整體有序序列。 歸併排序示例: 合併方法: 設r[
演算法設計與分析------歸併排序求序列最小值問題
題目要求:用分治法實現找一個序列最小值的功能那我剛學演算法,就引用書上的程式碼寫這個程式。書籍:《演算法設計與分析》(第2版)#include<iostream>using namespace std;void Merge(int r[],int r1[],int