TimusOJ - 1353. Milliard Vasya’s Function(DP)

題目連結

題目

求1到10⁹ ( [1, 10⁹] )中各位數字之和為S的數有多少個；

解析

這個題目和LeetCode - 518. Coin Change 2非常的相似。

遞迴(記憶化)的寫法:

• 總共需要9位數字，我們就去遞迴每一個位置可以累加0 ~ 9之間的數；
• 遞迴終止條件就是當夠了9個數字的時候，判斷現在累加的和是不是S即可了；
• 然後遞迴加上記憶化即可。

import java.io.BufferedInputStream;
 

import java.util.Arrays;
import java.util.Scanner;

public class Main {

    static int dp[][];

    static int recur(int pos, int sum, int S) {
        if (pos == 10) // 列舉9位數
            return S == sum ? 1 : 0;
        if (dp[pos][sum] != -1)
            return dp[pos][sum];
        int res = 0;
        for
 
 (int i = 0; i <= 9; i++) {
            sum += i;
            res += recur(pos + 1, sum, S);
            sum -= i;
        }
        return dp[pos][sum] = res;
    }

    public static void main(String[] args) {

        Scanner cin = new Scanner(new BufferedInputStream(System.in));
        int S =
 
 cin.nextInt();
        dp = new int[10][82];

        for (int i = 0; i < 10; i++)
            Arrays.fill(dp[i], -1);

        int res = recur(1, 0, S);
        if (S == 1) // notice 1000000000
            res += 1;
        System.out.println(res);
    }
}

其中遞迴函式 sum值也可以這麼寫，即不改變sum值:

static int recur(int pos, int sum, int S) {
    if (pos == 10) // 列舉9位數
        return S == sum ? 1 : 0;
    if (dp[pos][sum] != -1)
        return dp[pos][sum];
    int res = 0;
    for (int i = 0; i <= 9; i++)
        res += recur(pos + 1, sum + i, S);
    return dp[pos][sum] = res;
}

然後就是遞迴的反方向了，即改成dp動態規劃。

轉成dp陣列:

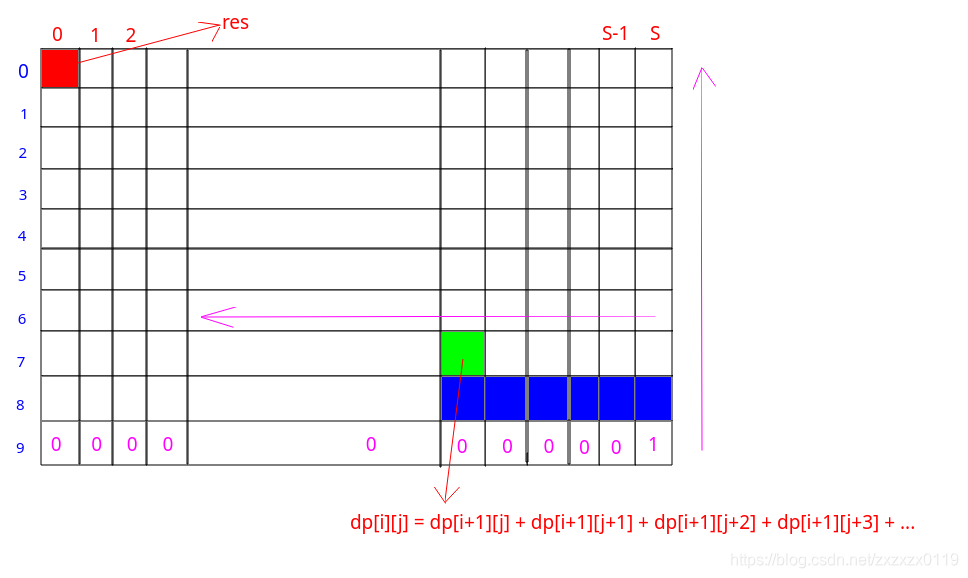
import java.io.BufferedInputStream;
import java.util.Arrays;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {

        Scanner cin = new Scanner(new BufferedInputStream(System.in));
        int S = cin.nextInt();
        int[][] dp = new int[10][S+1];

        for (int j = 0; j <= S; j++) // dp[9][S] = 1 , dp[1~S) = 0
            dp[9][j] = j == S ? 1 : 0;
        int sum = 0;
        for (int i = 8; i >= 0; i--) {
            for (int j = S; j >= 0; j--) {
                sum = 0;
                for (int k = 0; k <= 9; k++)
                    if (j + k <= S)
                        sum += dp[i + 1][j + k];
                dp[i][j] = sum;
            }
        }
        if(S == 1)
            dp[0][0]++;
        System.out.println(dp[0][0]);
    }
}

上面的方式是從 sum = 0開始遞迴的，也可以反方向從sum = S開始遞迴，遞迴和dp的程式如下:

import java.io.BufferedInputStream;
import java.util.Arrays;
import java.util.Scanner;

public class Main {

    static int dp[][];

    static int recur(int pos, int sum) {
        if (pos == 10) // 列舉9位數
            return sum == 0 ? 1 : 0;
        if (dp[pos][sum] != -1)
            return dp[pos][sum];
        int res = 0;
        for (int i = 0; i <= 9; i++)
            if(sum - i >= 0)
            res += recur(pos + 1, sum - i);
        return dp[pos][sum] = res;
    }

    public static void main(String[] args) {

        Scanner cin = new Scanner(new BufferedInputStream(System.in));
        int S = cin.nextInt();
        dp = new int[10][S+1];

        for (int i = 0; i < 10; i++)
            Arrays.fill(dp[i], -1);

        int res = recur(1, S);

        if (S == 1) // notice 1000000000
            res += 1;
        System.out.println(res);
    }
}

同樣轉換矩陣:

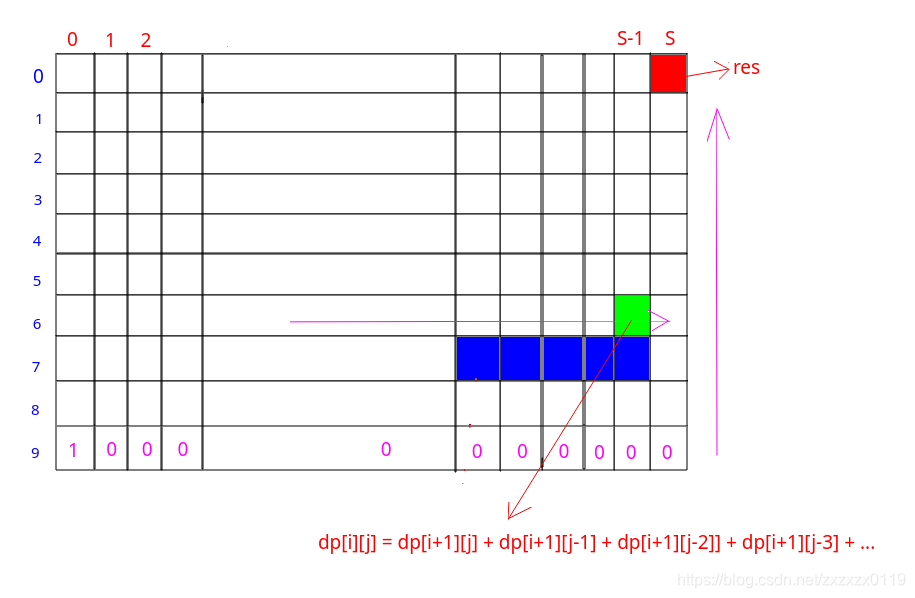
import java.io.BufferedInputStream;
import java.util.Arrays;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {

        Scanner cin = new Scanner(new BufferedInputStream(System.in));
        int S = cin.nextInt();
        int[][] dp = new int[10][S+1];

        for (int j = 0; j <= S; j++) // dp[9][S] = 1 , dp[1~S) = 0
            dp[9][j] = j == 0 ? 1 : 0;
        int sum = 0;
        for (int i = 8; i >= 0; i--) {
            for (int j = 0; j <= S; j++) {
                sum = 0;
                for (int k = 0; k <= 9; k++)
                    if (j - k >= 0)
                        sum += dp[i + 1][j - k];
                dp[i][j] = sum;
            }
        }
        if(S == 1)
            dp[0][S]++;
        System.out.println(dp[0][S]);
    }
}