機器學習演算法彙總大梳理
多分類問題優先選擇SVM,隨機森林,其次是邏輯迴歸。
樸素貝葉斯和線性迴歸都是比較簡單的模型,對於資料的要求比較高,功能不是特別強大。
1、決策樹
不需要對資料做任何預處理,
2、隨機森林
3、資料預處理與特徵工程
(1)資料預處理:只需要X
- 資料無量鋼化:標準化(轉化為正態分佈)、歸一化(不改變資料原始分佈,改變範圍,預設(0-1))
- 處理缺失值:可用均值、眾數、中位數、其他字元型或者數值型值填補
- 處理分型別變數:使用編碼處理字元型變數。一般對於有序變數或者有距變數可使用普通的編碼方式;對於名義變數採用獨熱編碼方式將其轉化為啞變數。
- 處理連續型變數:二值化、分箱。
另外還有去除重複值、處理異常值,樣本不均衡等問題。
預處理中大部分功能都是為了使資料滿足模型的需求,但是資料的無量綱化有著特殊的功能:在梯度和矩陣為核心的演算法中,譬如邏輯迴歸,支援向量機,神經網路,無量綱化可以加快求解速度;而在距離類模型,譬如K近鄰,K-Means聚類中,無量綱化可以幫我們提升模型精度,避免某一個取值範圍特別大的特徵對距離計算造成影響。
(2)特徵選擇:
- 方差過濾:去除區分度較低的特徵。(只需要X)
- 相關性檢驗:去除與標籤y相關性較低的特徵,卡方檢驗、F檢驗、互資訊法。(需要X和Y)
- Embedded嵌入法:利用 SelectFromModel和真正所需模型,以及X,Y
- Wrapper包裝法:利用RFE,結合任意一種模型,以及X,Y
(3)一般我們是先分訓練集和測試集,再進行資料預處理或者特徵選擇。
- 處理訓練集時:只用訓練集,因為我們不能夠把測試集資料的任何資訊帶入到模型中,如果在填補缺失值的時候用所有資料的均值來進行填補,就相當於把測試集的資料帶入到了模型中。
- 處理測試集時:只用訓練集,有些時候測試集非常小甚至只有一條資料,這時候就無法計算它的統計量資訊,我們可以用訓練集fit模型,然後用該模型處理測試集。或者對於fit模型不需要Y資料的資料預處理和特徵選擇方法也可以使用全資料fit,然後應用於測試資料。
4、降維演算法
(1)PCA是一種無監督學習算法,是將較多維的特徵對映到較少維空間的方法。
(2)PCA通過特徵值分解得到對角矩陣∑(對角元素是方差)來找出空間V,PCA使用方差作為資訊量的衡量指標。
(3)SVD使用奇異值分解得到對角矩陣∑(對角元素是奇異值)來找出空間V,SVD中用奇異值來衡量特徵上的資訊量的指標
(4)無論是PCA和SVD都需要遍歷所有的特徵和樣本來計算資訊量指標,因此計算緩慢。
(5) sklearn將降維流程拆成了兩部分:一部分是計算特徵空間V,由奇異值分解完成,另一部分是對映資料和求解新特徵矩陣(衡量指標是方差),由主成分分析完成,實現了用SVD的性質減少計算量,卻讓資訊量的評估指標是方差。
5、邏輯迴歸(基於概率,最大似然,梯度下降求引數)
(1)邏輯迴歸是基於概率的模型,對於每一個樣本有函式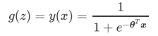 該函式是對樣本的預測結果。原理為:通過引入聯絡函式(Sigmoid函式)將線性迴歸的結果對映至(0,1)之間,且當g(z)接近0時樣本的標籤為類別0,當g(z)接近1時樣本的標籤為類別1,這樣就得到了一個分類模型。且邏輯迴歸可以不僅可以得到分類結果還可以計算得分,可用於製作評分卡。
該函式是對樣本的預測結果。原理為:通過引入聯絡函式(Sigmoid函式)將線性迴歸的結果對映至(0,1)之間,且當g(z)接近0時樣本的標籤為類別0,當g(z)接近1時樣本的標籤為類別1,這樣就得到了一個分類模型。且邏輯迴歸可以不僅可以得到分類結果還可以計算得分,可用於製作評分卡。
(2)利用二元邏輯迴歸的一般形式Yθ(x),使用最大似然法(即是使得所有樣本都預測正確)和推倒出邏輯迴歸的損失函式:
(3)我們只要追求損失函式的最小值,就能讓模型在訓練資料上的擬合效果最好,預測損失最低。用梯度下降法求損失函式的最小值(小球的例子),對其中的引數θ求導得到梯度向量:
梯度向量的反方向即是損失函式下降最快的方向,有關於θ的迭代函式:
其中α是步長,α*d代表自變數θ每次迭代移動的距離,-d的方向代表其移 動的方向。迭代得到使得損失函式最小的θ就是要求的引數。
(4)正則化:雖然邏輯迴歸和線性迴歸是天生欠擬合的模型,但我們還是需要控制過擬合的技術來幫助我們調整模型,對邏輯迴歸中過擬合的控制,通過正則化來實現。
(5)邏輯迴歸數學原理理解較為複雜,且它原理中的類概率並不是真正意義上的概率,但是由於計算速度快,對線性關係的擬合非常好,所以還是受到了青睞。
6、聚類演算法—Kmeans(基於距離,內聚外遠,迭代)
(1)對於無監督學習演算法,我們無法通過真實值與預測值的比較來衡量模型的好壞。因為無監督學習本身是對資料的一種探索,我們需要根據實際的業務需求來選取聚類結果。
(2) Inertia,簇內距離平方和。是衡量聚類的一個指標,我們可以近似將其看作損失函式。這是因為對於求參的模型(例如邏輯迴歸-梯度下降、線性迴歸-最小二乘(or梯度下降),SVM-梯度下降等)我們可以通過最小化損失函式的方法來得到好的模型引數,而在KMeans中,我們在一個固定的簇數K下,最小化總體平方和來求解最佳質心,並基於質心的存在去進行聚類。(雖然在聚類迭代的過程沒有計算inertia,但是在質心不斷變化不斷迭代的過程中,總體平方和是越來越小的,我們可以使用數學來證明,當整體平方和最小的時候,質心就不再發生變化了)
(3)但是inertia作為聚類的衡量指標但是其有許多缺點,例如沒有範圍,會隨著k的增大而減小(不是客觀的衡量指標)、對於資料分佈有假設等缺點,所以引入了輪廓係數(範圍-1~1之間)作為Kmeans的衡量指標。
7、SVM(基於距離,最大化邊際)
(1) 支援向量機原理:
用一個n-1維的超平面將資料分隔開,這個超平面叫做決策邊界,所有的樣本點不僅分佈在超平面兩側,而且分佈在兩側的虛線外側,兩個虛線超平面之間的距離叫做邊際。
決策邊界:
分類函式: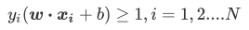
損失函式和約束條件: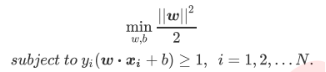
為了求得在約束條件下,損失函式得到最小值時候的w和b,我們採用拉格朗日乘子法(在滿足KKT條件的前提下)和對偶函式將 損失函式和約束條件轉化為:
此時新的決策邊界: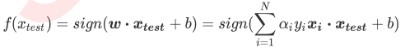
具體方法為:對拉格朗日函式的w和b分為求導,得到結果帶入對偶函式。
然後對目標函式利用梯度下降法或者SMO或者二次規劃等方法求得α,結合上面的式子也可以得到w和b。
(2) SVM四種核函式選擇:
通過實踐進行選擇,直接上各種核跑資料,看得分。
1. 線性核,尤其是多項式核函式在高次項時計算非常緩慢(SVM是基於距離的)
2. rbf和多項式核函式都不擅長處理量綱不統一的資料集
這兩點都可以通過資料標準化來解決,(無量綱化資料既可以提升有關梯度下降類模型的求解速度,又可以提升有關距離類模型的精度)
(3)SVM調參
| 核函式 |
可調引數 |
調參方法 |
| Liner |
無 |
無 |
| Rbf |
Gamma |
學習曲線 |
| Sigmoid |
Gamma、coef0 |
網格搜尋 |
| Poly |
Gamma、coef0、degree |
網格搜尋 |
(4)SVM的軟間隔
較大的邊際使得模型有更好的泛化性。但是較大的邊際又會讓部分訓練樣本出現分類錯誤,因此引入軟間隔,在保證較大邊際的前提下,允許部分訓練樣本出現錯分,但是不能錯的離譜,讓決策邊界能夠忍受一部分的訓練誤差。即平衡“最大化邊際”(保證較大泛化誤差)和“最大化模型準確率”(保證較小訓練誤差)兩者。
C就是調節軟間隔程度的引數:C越大,儘量正確分類樣本;C越小,儘量最大化邊界。
在軟間隔中支援向量是αi(yi(wTxi+b)-1+ξi)=0 成立且αi>0(即αi≠0)的樣本點(那些αi=0的點就是被正確分類且在yi(w*xi+b)=1內側的點,也就不是支援向量,對決策超平面沒有任何影響),這些點由於各自αi和ζi的不同,可以位於在間隔邊界((yi(w*xi+b)=1))上、間隔邊界與決策超平面之間、或者在超平面誤分的一側,這些支援向量共同決定決策超平面的位置。
(5) 不平衡樣本的評估指標
SVM處理樣本不均衡情況比較擅長,因為SVC的引數class_weight和fit介面的引數sample_weight都比較容易調參。對於不平衡樣本就不能簡單的用score來評價模型的好壞了,因為如果少數樣本非常少,那即是模型把所有樣本都判斷為多數類,模型的分數仍然可以很高,但是存在樣本不平衡的場景中,判斷錯誤少數類的代價一般是比較高的。因此引入了很多種類的模型例如:cm,accuracy,precision,recall,F1 score,specificity,FPR,ROC,AUC等。對於邏輯迴歸,SVM等有置信度這一概念的模型,還可以利用ROC面積求解最佳閾值,微調模型,使其具有更高的recall和更低的FPR。
8、線性迴歸
(1)手推線性迴歸使用最小二乘法求解w,但是這涉及到矩陣求逆,運算量大,大多數還是使用梯度下降的方法迭代求w。
(2)對於迴歸類模型,由於其不像分型別模型那樣,只有預測正確預測錯誤這一評估方式;對於迴歸類模型我們想讓其更好的擬合原始資料,即預測值與真實值相差越少,並且模型能夠很好的描繪資料的原始分佈以及趨勢。
1、是否預測了正確的數值。使用RSS-殘差平方和可以衡量對於所有訓練樣本,預測值與真實值相差多少,但是由於其沒有界限,我們沒辦法根據RSS值直觀判斷模型好壞,故引入MSE-均方誤差,將RSS平分至每一個樣本,這樣可以將其與樣本最大值和最小值分別 進行比較,評判模型好壞。可以使用metrics模組中的MES模組,或者設定cross_val_score中的“neg_mean_squared_error”引數得到MSE分數。
2、是否擬合的足夠的資訊(資料分佈)。使用或者EVS-可解釋性方差分數(explained_varience_score)來衡量模型沒有已經捕捉到的資訊,有三種方式來呼叫,一種是直接從metrics中匯入r2_score,輸入真實值和預測值後打分。第二種是直接從線性迴歸 LinearRegression的介面score來進行呼叫。第三種是在交叉驗證中,輸入"r2"來呼叫。EVS有兩種呼叫方法,可以從metrics中匯入explained_varience_score呼叫,也可以在交叉驗證中輸入”explained_variance“來呼叫。
3、其實可以為一個負數,此時說明資料預處理過程或者建模過程傷害了資料本身或者模型效果非常不好需要更換模型。
9、樸素貝葉斯
(1)因為樸素貝葉斯是基於概率的演算法,因此需要的樣本量較小,因為一個較小的樣本基本就可以反映整個資料集的情況。
(2)樸素貝葉斯在計算的時候並不是既計算全概率公式,又計算類概率公式,而是隻計算類概率公式的值,因為對於不同的後驗概率來說,其公式中的分母的值都是全概率公式,是一樣的,只要比較不同類概率的大小就是後驗概率的大小了,而且各個類概率之和就是全概率。
(3)樸素貝葉斯是假設各個特徵之間是相互獨立的,因此計算類概率的時候是各個特徵分別計算的。
