非線性問題

在之前學了線性支援向量機，通過訓練集學習到分離超平面 $wx+b=0$，但是有時候分類問題不是線性的，也就是我們不能直接得到分離超平面。看下面兩個圖:

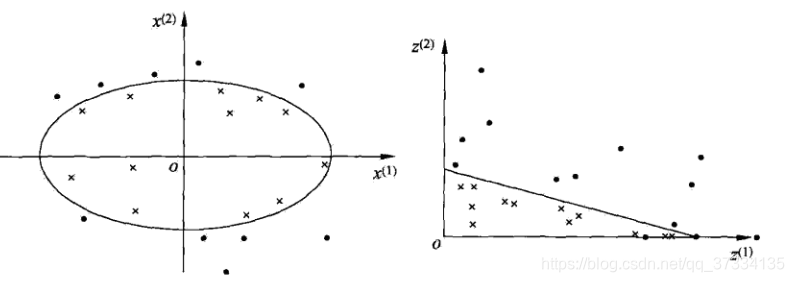
左邊的圖，只能使用一個橢圓（曲面）來對正例（黑點表示的例項）和負例（x表示的例項）來進行劃分，而無法使用超平面 $wx+b=0$

1. 使用一個函式，將原空間中的資料變對映到新空間（上圖中左圖中例項對映到右圖）;
2. 在新空間裡用線性分類學習方法學習到分類模型（這裡就是使用線性支援向量機學習到超平面 $wx+$
   b = 0 wx+b=0 ）。

核技法用到支援向量機中的思想：使用一個非線性變換將輸入空間對映到特徵空間，從而使得輸入空間的超曲面對應於特徵空間的超平面。

說到這就正式給出核函式的定義：

核函式：
令 $\chi$為輸入空間， $H$為特徵空間，如果存在一個 $\chi$ 到 $H$的對映

$\phi(x):\chi->H$

使得對於所有的輸入 $x,z\in\chi$滿足條件

$K(x,z)=\phi(x)\cdot\phi(z)$

則稱 $K(x,z)$為核函式， $\phi(x)$為對映空間， $\phi(x)\cdot\phi(z)$表示兩者的內積。

核技法在SVM中的使用

現在將核技法使用到非線性分類問題中，非線性支援向量機模型（凸二次規劃對偶模型）如下：

$\max\limits_{\alpha,\beta}-\frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_j<x_i,x_j>+\sum\limits_{i=1}^{N}\alpha_i$

$s.t.\qquad \sum\limits_{i=1}^{N}\alpha_iy_i=0\qquad (5)$

$\qquad \qquad0\leq\alpha_i\leq C$

求得的分離超平面如下：

$\sum\limits_{i=1}^{N}\alpha^*_iy_i<x,x_i>+b^*=0$

其中 $<x_i,x_j>$表示兩個向量的內積。
不管是對偶模型還是求得的結果都是輸入向量的內積，將其替換成核函式得到目標函式與分離超平面，得到：

$\max\limits_{\alpha,\beta}-\frac{1}{2}\sum\limits_{i=1}^{N}\sum\limits_{j=1}^{N}\alpha_i\alpha_jy_iy_jK(x_i,x_j)+\sum\limits_{i=1}^{N}\alpha_i$

$\sum\limits_{i=1}^{N}\alpha^*_iy_iK(x_i,x_j)+b^*=0$

其中 $K(x_i,x_j)=\phi(x_i)\cdot\phi(x_j)$