學習資料：《統計學習方法》，《機器學習》(周志華)，韓小陽ppt，鄒博ppt。

決策樹是一種樹形結構，對例項進行分類和迴歸的，下面主要說的是用來進行分類，最後說道CART的時候也會說到決策樹用到迴歸問題上。

1、決策樹模型與學習

先給出分類決策樹模型定義：是一種對例項資料進行分類的樹形結構，由節點和有向邊組成，而節點分為內部節點和葉節點。內部節點為特徵，葉子節點為分類結果，有向邊則根據特徵將資料集進行劃分。

舉個媽媽為女兒相親的例子。媽媽收集了很多相親的例子，女方會根據男方的特徵判斷會不會去相親，最後得到了下面的關於是否去相親的模型（該例子和圖來自與韓小陽製作的ppt）。

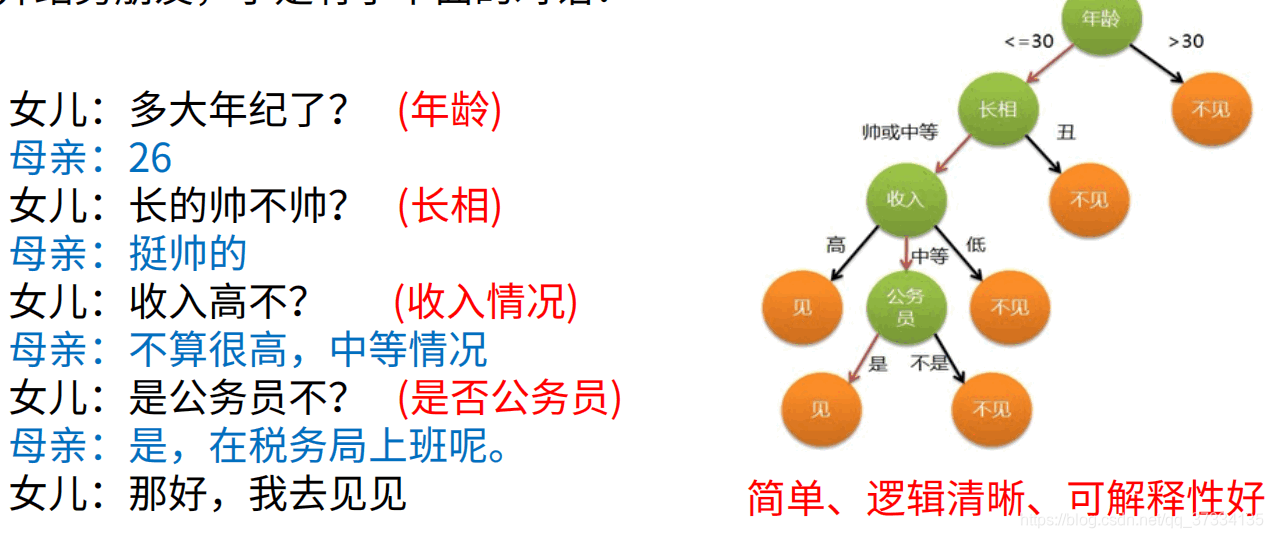
上面的樹即為分類決策樹模型，而媽媽根據以往的很多資料然後學習得到該模型的過程則是分類決策樹的學習過程，而上圖左側的談話則是根據已有的樹模型對新資料進行預測。好了，現在給出標準的決策樹的學習定義。

決策樹學習：假設給定訓練資料集

$D=\left\{\right(x_{}$

1 , y 1 ) , ( x 2

, y 2 ) , . . . , ( x n , y n ) } D=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\}

其中 $x_i=(x_i^1,x_i^2,...,x_i^m)$為輸入例項（特徵向量，共m個特徵）, $y=\{1,2,\cdots,K\}$表示類別。學習的目標就是根據給定的資料集構建一個決策樹模型，使得能夠對例項進行正確的分類。

注意：得到的樹模型會有無窮多個，學習演算法得到的不是最優的而是次優的（選取最優的是個NP問題）。

決策樹學習演算法有3部分構成：

1. 特徵選擇
2. 決策樹的生成
3. 決策樹的剪枝

下面來分別講述

2、特徵選擇

假設現在有銀行貸款申請樣本資料集，我們需要根據該資料集進行決策樹的學習從而得到分類決策樹模型。

通常的做法是：從根節點開始，選一個最優的特徵作為根節點，根據特徵值的不同對資料集進行分割，對分割產生的子節點，再遞迴的進行分割，直到所有例項都屬於同一類別，或者沒有特徵可選了那就把當前節點作為葉節點。

圖中可以看到有4個特徵，那麼把哪個特徵作為根節點，然後來進行劃分呢？答案是使用資訊增益最大的那個特徵。下面介紹資訊增益

2.1、資訊增益

為了便於說明，先給出熵和條件熵的定義

熵：隨機變數不確定性的表現。設X是一個取值個數有限的隨機變數，概率分佈為 $P(X=x_i)=p_i,i=1,2,\dots,n$。那麼隨機變數X的是熵定義為

$H(X) = -\sum\limits_{i=1}^{n}p_i\cdot log{p_{i}}$

通常底數為2或者 $e$，式子中可以發現結果與X無關，僅與X的分佈有關，所以表示成 $H(p)=-\sum\limits_{i=1}^{n}p_i\cdot log{p_{i}}$,顯然是個大於等於0的數。值越大那麼不確定性越大，相反，如果結果是0那麼結果就是確定的。舉個例子，假設X是0-1分佈， $P(X=0)=p$，那麼熵 $H(p)=-(plogp+(1-p)log(1-p))$。當 $p=0$時， $H(p)=0$也就是結果是確定的，直觀上確實是這樣，因為0事件不可能發生，結果只會是1事件。下面給出 $H(P)$隨著 $p$的變化圖。

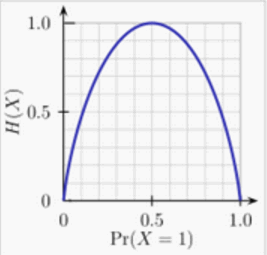
當 $p=0.5$的時候熵最大，直觀上容易理解，說明0,1等可能發生，結果是最難預測的。

設隨機變數(X,Y)，聯合概率分佈為
$P(X=x_i,Y=y_j)=p_{ij},i=1,2,\dots,n;j=1,2,\dots,m$
給出條件熵 $H(Y|X)$定義如下

條件熵：條件熵 $H(Y|X)$表示在已知隨機變數 $X$的條件下，隨機變數 $Y$的不確定性。定義為 $X$給定條件下 $Y$的條件概率分佈的熵對X的數學期望。

$H(Y|X)=\sum\limits_{i=1}^{n}p_i\cdot H(Y|X=x_i)$

其中 $p_i=P(X=x_i),i=1,2,...,n$。

資訊增益表示得知特徵X的資訊而使得類Y的資訊的不確定性減少的程度。

資訊增益：特徵A對訓練資料集D的資訊增益表示為 $g(D,A)$，定義為集合D的經驗熵 $H(D)$與特徵A給定條件下D的條件熵 $H(D|A)$之差，也可叫做互資訊。

$g(D,A)=H(D)-H(D|A)$

相關推薦