關於二叉樹的幾種遍歷方法
轉載請註明出處
http://blog.csdn.net/pony_maggie/article/details/38390513
作者:小馬
一 二叉樹的一些概念
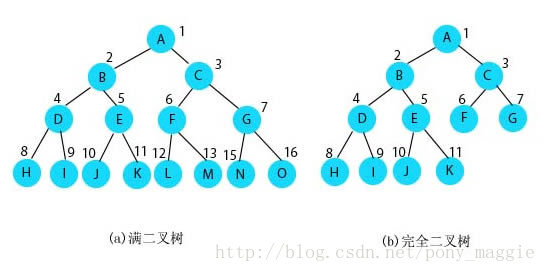
二叉樹就是每個結點最多有兩個子樹的樹形儲存結構。先上圖,方便後面分析。
1 滿二叉樹和完全二叉樹
上圖就是典型的二叉樹,其中左邊的圖還叫做滿二叉樹,右邊是完全二叉樹。然後我們可以得出結論,滿二叉樹一定是完全二叉樹,但是反過來就不一定。滿二叉樹的定義是除了葉子結點,其它結點左右孩子都有,深度為k的滿二叉樹,結點數就是2的k次方減1。完全二叉樹是每個結點都與深度為k的滿二叉樹中編號從1到n一一對應。
2 樹的深度
樹的最大層次就是深度,比如上圖,深度是4。很容易得出,深度為k的樹,擁有的最大結點數是2的k次方減1。
3 樹的孩子,兄弟,雙親
上圖中,B,C是A的孩子,B,C之間互為兄弟,A是B,C的雙親。
二如何建立二叉樹
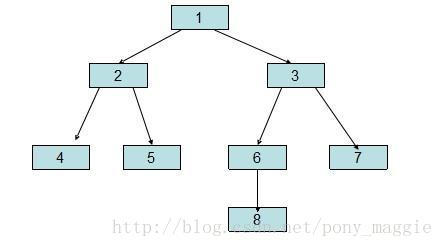
先說說二叉樹的儲存結構,跟很多其它模型一樣,也有順序和鏈式兩種方式。前者雖然使用簡單,但是存在浪費空間的問題,舉個例子,下圖的二叉樹,用順序的方式儲存(0表示空,沒有子樹)是:
1 2 3 4 5 6 7 0 0 0 0 8 0 0 0
是不是相當浪費空間呢。
鏈式結構可以定義如下:
typedef struct _BiTNode { int data; _BiTNode *leftChild; _BiTNode *rightChild; }BiTNode, *pBiTree;
然後就可以寫一個函式來建立二叉樹,過程是在控制檯輸入a表示退出當前這一層,不再為該層建立左右孩子。輸入其它字母表示繼續建立。比如下面的輸入序列:
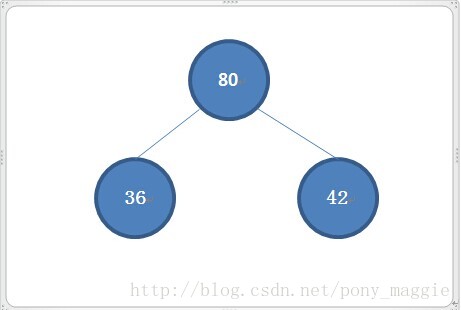
建立瞭如下結構的二叉樹,
每個結點裡的數值是隨機生成的小於100的數字。同時我也寫了一個自動的命令序列函式,方便測試,不用手動輸入,非自動和自動建立的函式如下:
//建立二叉樹, 先序順序 int CreateBiTree(pBiTree *root) { char ch = 0; fflush(stdin); if ((ch = getchar()) == 'a')//控制樹的結構 { *root = NULL; } else { *root = (BiTNode *)malloc(sizeof(BiTNode)); if (!(*root)) { return RET_ERROR; } (*root)->data = GetRandom(); CreateBiTree(&(*root)->leftChild); CreateBiTree(&(*root)->rightChild); } return RET_OK; } int g_i = 0; //建立二叉樹,自動執行,方便測試 int CreateBiTreeAuto(pBiTree *root) { char szOrder[] = "bbaabaa"; char ch = 0; if (szOrder[g_i++] == 'a')//控制樹的結構 { *root = NULL; } else { *root = (BiTNode *)malloc(sizeof(BiTNode)); if (!(*root)) { return RET_ERROR; } (*root)->data = GetRandom(); CreateBiTreeAuto(&(*root)->leftChild); CreateBiTreeAuto(&(*root)->rightChild); } return RET_OK; }
三遍歷順序
先序遍歷
先序遍歷是先訪問根結點,再左子樹,再右子樹,比如圖1中的右圖,先序遍歷的輸出如下:
A,B,D,H,I,E,J,K,C,F,G
根據上面的思想,很容易用遞迴的形式寫出先序遍歷的程式碼:
//先序遍歷
int PreOrderVisitTree(pBiTree T, VisitType pFuncVisit)
{
if (T)
{
(*pFuncVisit)(T->data);
if (PreOrderVisitTree(T->leftChild, pFuncVisit) == RET_OK)
{
if (PreOrderVisitTree(T->rightChild, pFuncVisit) == RET_OK)
{
return RET_OK;
}
}
return RET_ERROR;
}
else
{
return RET_OK;
}
}
中序遍歷和後序遍歷
有了先序的經驗,這兩個就很好理解了,中序是先訪問左子樹, 再根結點,再右子樹, 後序是先訪問左子樹, 再右子樹,再根結點。程式碼更容易,只要改一下呼叫順序就可以了。
不過我這裡給出一種非遞迴的實現。遞迴固然是清晰明瞭,但是存在效率低的問題,非遞迴的方案用棧結構來存結點資訊,通過出棧訪問來遍歷二叉樹。它思想是這樣的,當棧頂中的指標非空時,遍歷左子樹,也就是左子樹根的指標進棧。當棧頂指標為空時,應退至上一層,如果是從左子樹返回的,訪問當前層,也就是棧頂中的根指標結點。如果是從右子樹返回,說明當前層遍歷完畢,繼續退棧。程式碼如下:
//中序遍歷, 非遞迴實現
int InOrderVisitTree(pBiTree T, VisitType pFuncVisit)
{
ponyStack binaryTreeStack;
InitStack(&binaryTreeStack, 4);
Push(&binaryTreeStack, &T);
pBiTree pTempNode;
while (!IsEmptyStack(binaryTreeStack))
{
while((GetTop(binaryTreeStack, &pTempNode) == RET_OK) && (pTempNode != NULL))
{
Push(&binaryTreeStack, &(pTempNode->leftChild));
}
Pop(&binaryTreeStack, &pTempNode);
if (!IsEmptyStack(binaryTreeStack))
{
Pop(&binaryTreeStack, &pTempNode);
(*pFuncVisit)(pTempNode->data);
Push(&binaryTreeStack, &(pTempNode->rightChild));
}
}
return RET_OK;
}
程式碼下載地址:
http://download.csdn.net/detail/pony_maggie/7714493
或
https://github.com/pony-maggie/BinaryTreeDemo
相關推薦
二叉樹幾種遍歷方式之間的轉換
寫在前面 二叉樹的遍歷方式,基本可以歸結為四種:前序遍歷、中序遍歷、後序遍歷、層次遍歷 先序遍歷順序:根,左兒子,右兒子 中序遍歷順序:左兒子,根,右兒子 後序遍歷順序:左兒子,右兒子,根 層次遍歷順序:根據每一層的順序,由左向右依次輸出 遍歷順序及轉換 &n
二叉樹幾種遍歷演算法
<span style="font-size:14px;">/*二叉樹的遍歷*/ #include <iostream> #include <cstring> #include <stack> using namespace
二叉樹三種遍歷方式
二叉樹的遍歷,如果是手工畫圖,還可以使用投影法快速得到遍歷序列。 以下圖二叉樹為例,講解投影法快速得到遍歷序列的過程。 (1) 中序遍歷 中序遍歷就像在無風的情況下,太陽直射
【圖解資料結構】 一組動畫徹底理解二叉樹三種遍歷
二叉樹的遍歷是指從根結點出發,按照某種次序依次訪問二叉樹中所有結點,使得每個結點被訪問一次且僅被訪問一次。 在二叉樹的遍歷中存在三種較為常用的遍歷方式:前序遍歷、中序遍歷、後序遍歷。接下來我將嘗試著用三組動畫向讀者詳細的介紹這三種遍歷方式的邏輯思路,希望讓讀者看到任何的二叉樹都能在腦海中快速的勾勒出動畫。
二叉樹三種遍歷方式及通過兩種遍歷重構二叉樹(java實現)
重構方法參考文章【重構二叉樹(Java實現):https://blog.csdn.net/wangbingcsu/article/details/51372695】 文章目錄 二叉樹類 三種遍歷方式 前序遍歷 中序遍歷 後序遍歷
Java實現二叉樹三種遍歷演算法
</pre><p></p><p>參考網上一些資料測試整理了一下二叉樹遍歷的Java實現程式碼。</p>二叉樹三種遍歷方式:先序遍歷、中序遍歷、後序遍歷。<p>首先定義二叉樹類:</p>&l
二叉樹的多種遍歷方法
二叉樹遍歷學習 1.給出滿二叉樹的前序遍歷建樹。 #include <stdio.h> #include <stdlib.h> //前提是已知樹是滿的 char cach
二叉樹三種遍歷方式的遞迴和迴圈實現
轉載自:http://blog.csdn.net/pi9nc/article/details/13008511 二叉樹是一種非常重要的資料結構,很多其他資料機構都是基於二叉樹的基礎演變過來的。二叉樹有前、中、後三種遍歷方式,因為樹的本身就是用遞迴定義的,因此採用遞迴的方
二叉樹3種遍歷演算法遞迴與非遞迴實現詳解
一, 二叉樹先序遍歷的實現 遞迴實現 void PreOrderTraverse(BiTree T) { if( T ) { VisitF(T->data);//訪問根節點 PreOrderTra
二叉樹三種遍歷六種實現
二叉樹是一種非常重要的資料結構,很多其他資料機構都是基於二叉樹的基礎演變過來的。二叉樹有前、中、後三種遍歷方式,因為樹的本身就是用遞迴定義的,因此採用遞迴的方法實現三種遍歷,不僅程式碼簡潔且容易理解,但其開銷也比較大,而若採用非遞迴方法實現三種遍歷,則要用棧來模擬實現
二叉樹三種遍歷遞迴及非遞迴實現
二叉樹的三種遍歷方式包括: 前序遍歷中序遍歷後序遍歷 三種遍歷的遞迴方法都非常好實現,而且簡單易懂。非遞迴實現也是通過使用棧來模擬遍歷的過程。順便提一句,能用遞迴做的,基本都能用棧來實現。前序遍歷和中序遍歷的非遞迴寫法相對比較簡單,只需要模擬遍歷過程即可。後序遍歷非遞迴寫
二叉樹四種遍歷方式的速度差異
同學阿里三面面試官的一道面試題是:二叉樹每個節點都儲存一個整數,想要求所有節點數值之和,哪種遍歷方式最快? 首先定義二叉樹 struct Tree { int val; Tree *left; Tree *right; Tre
二叉樹三種遍歷 (Java)
以前學資料結構的時候是用C學的,現在重新複習一下資料結構裡用的比較多的二叉樹,用Java實現。好啦,廢話不多說啦!! 我們知道二叉樹有三種遍歷方式:前序(根左右)、中序(左根右)、後序(左右根)。每種遍歷方式其實就是一個遞迴呼叫。 步驟: 1、將陣列中的元素賦值給二叉樹(通
二叉樹三種遍歷的非遞迴思路(JAVASCRIPT)
二叉樹在圖論中是這樣定義的:二叉樹是一個連通的無環圖,並且每一個頂點的度不大於3。有根二叉樹還要滿足根結點的度不大於2。有了根結點之後,每個頂點定義了唯一的父結點,和最多2個子結點。然而,沒有足夠的資訊來區分左結點和右結點。如果不考慮連通性,允許圖中有多個連通分
二叉樹三種遍歷方式,先序、中序、後序
二叉樹遍歷方式分為三種:先序,中序和後序。 可以以根節點的位置為參考來記遍歷方式,在第一個為先序,中間為中序,最後為後序; 即:先序: 根左右;中序:左根右;後序:左右根。 借個圖: 每個節點左上角,底部,右上角分別對應先序,中序,後序時的取值點
二叉樹三種遍歷非遞迴演算法
1.先序遍歷非遞迴演算法 #define maxsize 100 typedef struct { Bitree Elem[maxsize]; int top; } SqStack; void PreOrderUnrec(Bitree t) { SqStack s; Stack
關於二叉樹的幾種遍歷方法
轉載請註明出處 http://blog.csdn.net/pony_maggie/article/details/38390513 作者:小馬 一 二叉樹的一些概念 二叉樹就是每個結點最多有兩個子樹的樹形儲存結構。先上圖,方便後面分析。 1 滿二叉樹和完全二
二叉樹的幾種遍歷方法
三種遍歷方法, 前序:先根結點後左孩子最後右孩子 中序:先左孩子後根結點最後右孩子 後序:先左孩子後右孩子最後根結點 前序 先根結點後左孩子最後右孩子首先知道A為根節點把左側每個都看成一個獨立的樹可
Python實現"二叉樹的層次遍歷||"的一種方法
給定一棵二叉樹,返回從上到下按層級順序遍歷結點的值(例如,從葉子節點的層級到根結點的層級) 例如: 二叉樹[3,9,20,null,null,15,7], 3 / \ 9 20 / \ 15 7 返回它從下到上按層級順序遍歷的
層次遍歷二叉樹-三種不同的方法
給定一棵二叉樹,要求進行分層遍歷,每層的節點值單獨列印一行,下圖給出事例結構: 對此二叉樹遍歷的結果應該是: 1, 2 , 3 4, 5, 6 7, 8 第一種方法,就是利用遞迴的方法,按層進行列印,我們把根節點當做第0層,之後層次依次增加,如果我們想列印第二層怎麼辦呢,