為了進一步瞭解RB樹，先了解一下二叉查詢樹

定義：

二叉查詢樹是一棵二叉樹，因此可以用鏈式結構來儲存資料。若二叉查詢樹不為空，則應具有以下性質：

1. 關鍵字的值唯一
2. 若左子樹不為空，則子樹任何節點關鍵字值一定小於其根節點的關鍵字值
3. 若右子樹不為空，則子樹任何節點關鍵字值一定大於其根節點的關鍵字值
4. 左、右子樹任然是二叉查詢樹

結構示意圖

查詢節點：

1. 若二叉查詢樹為空，則查詢失敗
2. 若該樹非空且查詢資料x等於根節點的值，則查詢成功，返回根節點
3. 若該樹非空且查詢資料x小於根節點的值，則查詢左子樹，直到值相等，並返回節點
4. 若該樹非空且查詢資料x大於根節點的值，則查詢右子樹，直到值相等，並返回節點

插入節點：

1. 若二叉查詢樹為空，則將結點作為根節點插入
2. 若所插入節點關鍵字值等於根節點的值，則插入失敗，並返回
3. 若所插入節點關鍵字值小於根節點的值，則把節點插入到左子樹中
4. 若所插入節點關鍵字值大於根節點的值，則把節點插入到右子樹中

刪除節點：

1. 若p結點為葉子結點，則刪去該葉子結點，修改其雙親結點的指標即可。
2. 若p結點只有左子樹PL或右子樹PR，此時只要令PL或PR直接成為其雙親結點的左子樹（當p是左子樹）或右子樹（當p是右子樹）。
3. 若p結點的左子樹和右子樹均不空。找出節點p的後繼節點y（一定在節點p的右子樹中），以右子樹中的最小數作為後繼節點。

下面是實現這些功能的程式

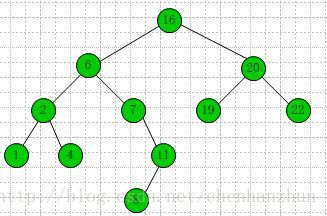
#include<stdio.h>
#include<stdlib.h>
#include<malloc.h>

#define LENGTH 11

struct BinSearNode
{
	int key;
	struct BinSearNode *left_child;
	struct BinSearNode *right_child;
	struct BinSearNode *parent;
}Node;
typedef struct BinSearNode *PNode;

/*Search the node of the tree*/
PNode Search_Tree(PNode root,int key)
{
	PNode x=root;
	//the tree is not empty and the key is not equal
	while(NULL!=x && x->key!=key)
	{
		if(x->key<key)
			x=x->right_child;//along the right child of tree,until it is empty
		else
			x=x->left_child;//along the left child of tree,until it is empty
	}
	return x;//return the node
}
/*the minimum key of node in the tree*/
PNode Minimum_Tree(PNode root)
{
	PNode x=root;
	while(NULL!=x->left_child)
	{
		x=x->left_child;
	}
	return x;
}
/*the maxmum key of node in the tree*/
PNode Maxmum_Tree(PNode root)
{
	PNode x=root;
	while(NULL!=x->right_child)
	{
		x=x->right_child;
	}
	return x;
}
/*the successor node of the x,後繼節點可以這麼理解，將查詢樹從小到大排序，比他大的值
如果有右孩子，那麼應該是右子樹當中的最小值
如果沒有右孩子，那麼應該向上追溯，直至一個分支節點是其父節點的左孩子，返回父節點
可以用於operate++*/
PNode Successor_Tree(PNode x)
{
	PNode y=NULL;
	//case 1:the right subtree of node x is not empty
	if(NULL!=x->right_child)
	{
		y=Minimum_Tree(x->right_child);
	}
	//case 2:the right subtree of node x is empty
	//and the node of x has a successor node y
	else
	{
		y=x->parent;
		while(NULL!=y && x==y->right_child) 
		{
			x=y;
			y=y->parent;
		}
	}
	return y;
}
/*the predecessor node of the x，前任節點
如果節點有左孩子，那麼找到左孩子的最大值
如果沒有左孩子，那麼向上追溯直至一個分支當前節點是對應父節點的右孩子，返回父節點的值
*/
PNode Predecessor_Tree(PNode x)
{
	PNode y=NULL;
	//case 1:the left subtree of node x is not empty
	if(NULL!=x->left_child)
	{
		y=Maxmum_Tree(x->left_child);
	}
	//case 2:the left subtree of node x is empty
	//and the node of x has a predecessor node y
	else
	{
		y=x->parent;
		while(NULL!=y && x==y->left_child)
		{
			x=y;
			y=y->parent;
		}
	}
	return y;
}

/*insert a new node into the BST*/
void Insert_Tree(PNode *root,int key)
{
	PNode x=*root;
	PNode y=NULL;
	PNode z=(PNode)malloc(sizeof(Node));//<開闢一個節點的空間
	if(NULL==z)
	{
		printf("malloc the z is failed.");
		exit(1);
	}
	//initial the node of z
	z->key=key;
	z->left_child=z->right_child=z->parent=NULL;
	//Find the location node of y to insert the node of z
	while(NULL!=x)
	{
		y=x; //<找到當前樹滿足條件的葉子節點了，表示為y，之後在y節點後面進行插入操作
		if(z->key<x->key)
			x=x->left_child;
		else
			x=x->right_child;
	}
	//insert the node of z
	z->parent=y;
	if(NULL==y)
		*root=z;//tree was empty
	else
	{
		if(z->key<y->key)
			y->left_child=z;
		else
			y->right_child=z;
	}
}
void Transplant(PNode *root,PNode u,PNode v)
{
	if(NULL==u->parent)
		*root=v;
	else
	{
		if(u==u->parent->left_child)
			u->parent->left_child=v;
		else
			u->parent->right_child=v;
	}
	if(NULL!=v)
		v->parent=u->parent;
}
/*delete a node in the binary search tree*/
void Delete_Tree(PNode *root,int key) //<刪除節點
{
	//Find the node you want to delete
	PNode p=Search_Tree(*root,key);
	if(NULL==p->left_child)
		Transplant(root,p,p->right_child);
	else
	{
		if(NULL==p->right_child)
			Transplant(root,p,p->left_child);
		else
		{
			PNode y=Successor_Tree(*root);
			if(y->parent!=p)
			{
				Transplant(root,y,y->right_child);
				y->right_child=p->right_child;
				y->right_child->parent=y;
			}
			Transplant(root,p,y);
			y->left_child=p->left_child;
			y->left_child->parent=y;
		}
	}
}
/*print the key of binary search tree*/
void ioder_Tree(PNode root)
{
	if(NULL!=root)
	{
		ioder_Tree(root->left_child);
		printf("  %d",root->key);
		ioder_Tree(root->right_child);
	}
}
int main()  
{  
	int i;  
	int Arr[LENGTH]={16,6,20,2,7,19,22,1,4,11,8};  
	PNode root=NULL;  
	PNode p=NULL;  
	for(i=0;i<LENGTH;i++)  
	{  
		Insert_Tree(&root,Arr[i]);  
	}  
	ioder_Tree(root);  
	printf("\n");  
	//printf("Hello world!\n");  
	Delete_Tree(&root,11);  
	ioder_Tree(root);  
	printf("\n");  
	p=Maxmum_Tree(root);  
	printf("The Maxmum of node is:%d\n",p->key);  
	p=Minimum_Tree(root);  
	printf("The Minimum of node is:%d\n",p->key);  
	return 0;  
}  
 

結果圖：

在STL中除了要求是搜尋二叉樹之外，還需要是平衡搜尋二叉樹：

因為關聯容器很重要的一個是搜尋效率

平衡樹有很多種比如AVL_tree,RB-tree,AA-tree

平衡二叉樹插入節點和刪除節點的平均時間都是比較長，但是他們可以很好的避免難以應付的最壞情況

AVL-tree要求任何節點的左右子樹的高度相差最多為1

如果插入或者刪除操作打破了這些平衡條件，那麼這樣的樹應該需要做相應的旋轉操作來達到平衡

RB-tree的節點有紅色和黑色的區分，並有一些限制條件，之後會專門進行介紹