sEMG專案總結(6)NinaPro肌電資料集(52類動作)
NinaPro肌電資料集(52類動作)
目錄
1sEMG Data
subjucts : 67 intact subjects & 11 trans-radial amputated subjects
Sensors : 10 Otto Bock (100HZ) & 12 Deslys (2KHZ)
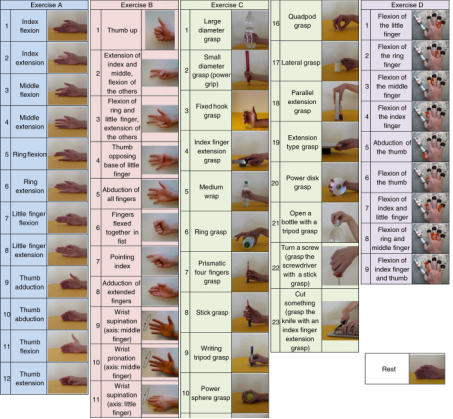
Methods : 5s movement & 3s rest (Repeat 10 times)
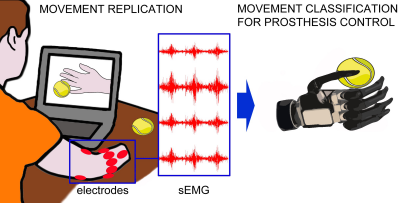
sEMG資料:
(1)使用廣義似然比演算法 離線重新標記標籤
(2)通過RMS校正,使得Delsys訊號與Otto Bock訊號類似,
之後訊號以200HZ下采樣,以減少計算時間
(3)都以 1HZ低通濾波
(4)預處理過程中還對幾個歸一化程式進行了測試
2簡單ANN分類
data: 10 channels (Otto bock)
features: 10 time-domain features
movement: 52 (remove rest)
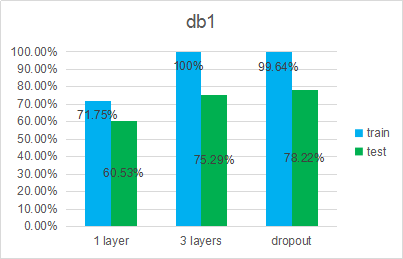
db1: before cutting (9047 samples)
db2: after cutting (4170 samples)(裁剪掉過度狀態、防止過擬合)
Neural Networks model
1 layer model: 100-52
3 layers model : 100-200-160-52
3 layers with dropout: keep_prob = 0.5
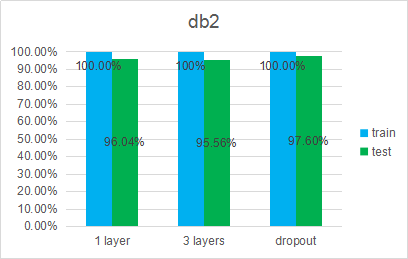
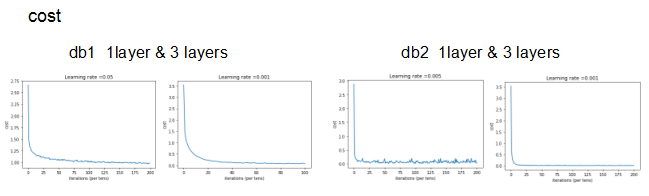
summary
- Before cutting the data, the accuracy is higher than the author’s highest accuracy.
- After cutting the data, the accuracy is greatly improved.
- Dropout has little effect on overfitting.
3層dropout分類
import math
import h5py
import scipy
import random
import scipy.io as scio
from "下載資料和標籤"
f = scio.loadmat('db1.mat')
data = f['features'][:,0:100]
label = f['features'][:,100]
"隨機打亂資料和標籤"
N = data.shape[0]
index = np.random.permutation(N)
data = data[index,:]
label = label[index]
"對資料特徵歸一化"
data = max_min_normalization(data)
"將label的資料型別改成int,將label的數字都減1"
label = label.astype(int)
label = label - 1
"轉換標籤為one-hot"
label = label.reshape((1,label.shape[0]))
label = convert_to_one_hot(label,52)
data = data.T
"生成訓練樣本及標籤、測試樣本及標籤"
num_train = round(N*0.8)
num_test = N-num_train
train_data = data[:,0:num_train]
test_data = data[:,num_train:N]
train_label = label[:,0:num_train]
test_label = label[:,num_train:N]
print("train data shape:",train_data.shape)
print("train label shape:",train_label.shape)
print("test data shape:",test_data.shape)
print("test label shape:",test_label.shape)
X_train = train_data
Y_train = train_label
X_test = test_data
Y_test = test_labeltrain data shape: (100, 7238)
train label shape: (52, 7238)
test data shape: (100, 1809)
test label shape: (52, 1809)
# 1-1、建立佔位符
def create_placeholders(n_x, n_y):
"""
Creates the placeholders for the tensorflow session.
Arguments:
n_x -- scalar, size of an image vector (num_px * num_px = 64 * 64 * 3 = 12288)
n_y -- scalar, number of classes (from 0 to 5, so -> 6)
Returns:
X -- placeholder for the data input, of shape [n_x, None] and dtype "float"
Y -- placeholder for the input labels, of shape [n_y, None] and dtype "float"
Tips:
- You will use None because it let's us be flexible on the number of examples you will for the placeholders.
In fact, the number of examples during test/train is different.
"""
X = tf.placeholder(tf.float32, shape = [n_x, None])
Y = tf.placeholder(tf.float32, shape = [n_y, None])
keep_prob = tf.placeholder("float")
return X, Y, keep_prob
# 1-2、初始化引數
def initialize_parameters():
"""
Initializes parameters to build a neural network with tensorflow. The shapes are:
W1 : [200, 100]
b1 : [200, 1]
W2 : [150, 200]
b2 : [150, 1]
W3 : [52, 150]
b3 : [52, 1]
Returns:
parameters -- a dictionary of tensors containing W1, b1, W2, b2, W3, b3
"""
tf.set_random_seed(1) # so that your "random" numbers match ours
W1 = tf.get_variable("W1", [160,100], initializer = tf.contrib.layers.xavier_initializer(seed = 1))
b1 = tf.get_variable("b1", [160,1], initializer = tf.zeros_initializer())
W2 = tf.get_variable("W2", [120,160], initializer = tf.contrib.layers.xavier_initializer(seed = 1))
b2 = tf.get_variable("b2", [120,1], initializer = tf.zeros_initializer())
W3 = tf.get_variable("W3", [52,120], initializer = tf.contrib.layers.xavier_initializer(seed = 1))
b3 = tf.get_variable("b3", [52,1], initializer = tf.zeros_initializer())
parameters = {"W1": W1,
"b1": b1,
"W2": W2,
"b2": b2,
"W3": W3,
"b3": b3}
return parameters
# 1-3、TensorFlow中的前向傳播
# tf中前向傳播停止在z3,是因為tf中最後的線性層輸出是被作為輸入計算loss,不需要a3
def forward_propagation(X, parameters, keep_prob):
"""
Implements the forward propagation for the model: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SOFTMAX
Arguments:
X -- input dataset placeholder, of shape (input size, number of examples)
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3"
the shapes are given in initialize_parameters
Returns:
Z3 -- the output of the last LINEAR unit
"""
W1 = parameters['W1']
b1 = parameters['b1']
W2 = parameters['W2']
b2 = parameters['b2']
W3 = parameters['W3']
b3 = parameters['b3']
Z1 = tf.add(tf.matmul(W1, X), b1) # Z1 = np.dot(W1, X) + b1
A1 = tf.nn.relu(Z1) # A1 = relu(Z1)
Z2 = tf.add(tf.matmul(W2, A1), b2) # Z2 = np.dot(W2, a1) + b2
A2 = tf.nn.relu(Z2) # A2 = relu(Z2)
A2_drop = tf.nn.dropout(A2, keep_prob)
Z3 = tf.add(tf.matmul(W3,A2_drop),b3)
A3 = Z3
return A3
# 1-4、計算成本函式
def compute_cost(A3, Y):
"""
Computes the cost
Arguments:
Z3 -- output of forward propagation (output of the last LINEAR unit), of shape (6, number of examples)
Y -- "true" labels vector placeholder, same shape as Z3
Returns:
cost - Tensor of the cost function
"""
# to fit the tensorflow requirement for tf.nn.softmax_cross_entropy_with_logits(...,...)
logits = tf.transpose(A3)
labels = tf.transpose(Y)
# 函式輸入:shape =(樣本數,類數)
# tf.reduce_mean()
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = logits, labels = labels))
return cost
# 1-6、建立模型
def model(X_train, Y_train, X_test, Y_test, learning_rate = 0.0001,
num_epochs = 3001, minibatch_size = 32, print_cost = True):
ops.reset_default_graph() # to be able to rerun the model without overwriting tf variables
tf.set_random_seed(1) # to keep consistent results
seed = 3 # to keep consistent results
(n_x, m) = X_train.shape # (n_x: input size, m : number of examples in the train set)
n_y = Y_train.shape[0] # n_y : output size
costs = [] # To keep track of the cost
X, Y ,keep_prob = create_placeholders(n_x, n_y)
parameters = initialize_parameters()
A3 = forward_propagation(X, parameters, keep_prob)
cost = compute_cost(A3, Y)
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost)
init = tf.global_variables_initializer()
# 開始tf會話,計算tf圖
with tf.Session() as sess:
sess.run(init)
for epoch in range(num_epochs):
epoch_cost = 0. # Defines a cost related to an epoch
num_minibatches = int(m / minibatch_size) # number of minibatches
seed = seed + 1
minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)
for minibatch in minibatches:
(minibatch_X, minibatch_Y) = minibatch
_ , minibatch_cost = sess.run([optimizer, cost], feed_dict = {X: minibatch_X, Y: minibatch_Y, keep_prob:0.5})
epoch_cost += minibatch_cost / num_minibatches
# Print the cost every epoch
if print_cost == True and epoch % 100 == 0:
print ("Cost after epoch %i: %f" % (epoch, epoch_cost))
correct_prediction = tf.equal(tf.argmax(A3), tf.argmax(Y))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print ("Train Accuracy:", accuracy.eval({X: X_train, Y: Y_train, keep_prob: 1}))
print ("Test Accuracy:", accuracy.eval({X: X_test, Y: Y_test, keep_prob: 1}))
if print_cost == True and epoch % 10 == 0:
costs.append(epoch_cost)
# plot the cost
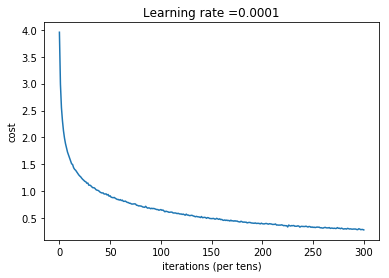
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title("Learning rate =" + str(learning_rate))
plt.show()
# 將parameters儲存在一個變數中
parameters = sess.run(parameters)
print ("Parameters have been trained!")
# Calculate the correct predictions
correct_prediction = tf.equal(tf.argmax(A3), tf.argmax(Y))
# Calculate accuracy on the test set
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print ("Train Accuracy:", accuracy.eval({X: X_train, Y: Y_train, keep_prob:1}))
print ("Test Accuracy:", accuracy.eval({X: X_test, Y: Y_test, keep_prob:1}))
return parameters
parameters = model(X_train, Y_train, X_test, Y_test)Parameters have been trained!
Train Accuracy: 0.985908
Test Accuracy: 0.77225
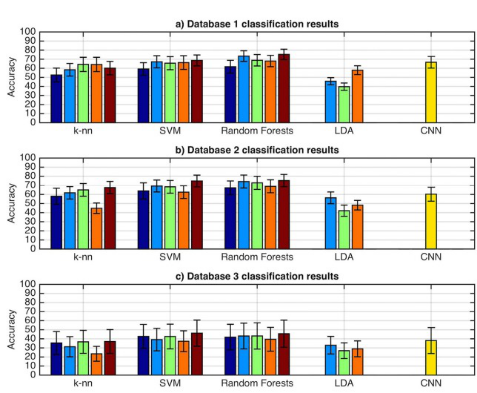
3Deep learning applied to Ninapro
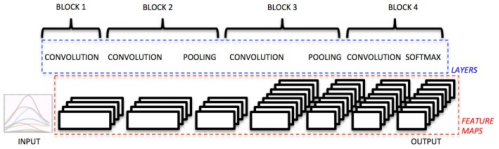
(1)輸入資料:對應於150ms的時間視窗,跨越所有的電極
分析時間視窗為了實時控制
(2)Block1: 32個濾波器卷積層 + ReLU
濾波器定義為一行,長度為電極數 (1*10)
(3)Block2: 32個濾波器 3*3 + ReLU + average Pool 3*3
(4)Block3: 64個濾波器 5*5 + ReLU + average Pool 3*3
(5)Block4: (Otto Bock)64個濾波器 5*1 + ReLU
(6)Block5: 濾波器大小 1*1 + softmax loss
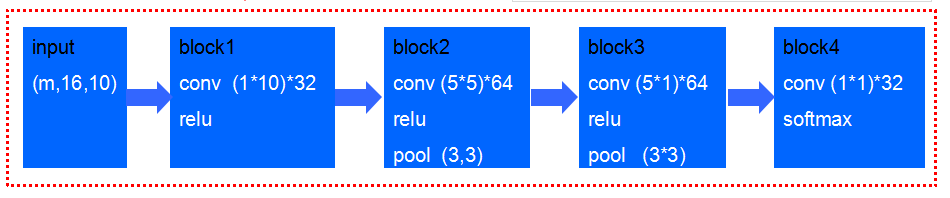
訓練:
(1)根據資料範圍,按照百分比初始化卷積層權重
(2)多次測試,使用隨機梯度下降,動量0.9,
學習率固定為0.001,權重衰減0.0005,batch_size=256,epoch=30
(3)使用資料增強:資料加倍,信噪比=25加入新資料
結果:
該表報告每個引數與相應的Top-5錯誤和時期獲得的最小Top-1錯誤。
測試了兩種不同的方法:
時間視窗歸一化(即,將每個時間視窗減去平均值併除以標準偏差)
基於訓練資料的歸一化(即,將所有時間視窗減去訓練資料的平均值並將其除以訓練資料標準偏差)
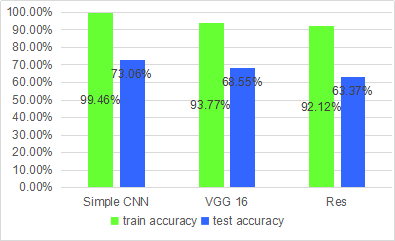
test accuracy 73.06% > 66.59 6.40% (author’s)
sample cnn
import math
import h5py
import scipy
import random
import scipy.io as scio
from PIL import Image
from scipy import ndimage
from tensorflow.python.framework import ops
import time
import tensorflow as tf
import numpy as np
import scipy.misc
import pydot
import matplotlib.pyplot as plt
from matplotlib.pyplot import imshow
from IPython.display import SVG
from keras import layers
from keras.layers import Input, Add, Dense, Activation, ZeroPadding2D, BatchNormalization, Flatten, Conv2D, AveragePooling2D, MaxPooling2D, GlobalMaxPooling2D
from keras.models import Model, load_model
from keras.preprocessing import image
from keras.initializers import glorot_uniform
from keras.applications.imagenet_utils import preprocess_input
from keras.utils import layer_utils
from keras.utils import plot_model
from keras.utils.data_utils import get_file
from keras.utils.vis_utils import model_to_dot
import keras.backend as K
K.set_image_data_format('channels_last')
K.set_learning_phase(1)
%matplotlib inline
np.random.seed(1)
def convert_to_one_hot(Y, C):
Y = np.eye(C)[Y.reshape(-1)].T
return Y
def max_min_normalization(data_array):
rows = data_array.shape[0]
cols = data_array.shape[1]
temp_array = np.zeros((rows,cols))
col_min = data_array.min(axis=0)
col_max = data_array.max(axis=0)
for i in range(0,rows,1):
for j in range(0,cols,1):
temp_array[i][j] = (data_array[i][j]-col_min[j])/(col_max[j]-col_min[j])
return temp_array
def random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):
"""
Creates a list of random minibatches from (X, Y)
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (containing 0 if cat, 1 if non-cat), of shape (1, number of examples)
mini_batch_size - size of the mini-batches, integer
seed -- this is only for the purpose of grading, so that you're "random minibatches are the same as ours.
Returns:
mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
"""
m = X.shape[1] # number of training examples
mini_batches = []
np.random.seed(seed)
# Step 1: Shuffle (X, Y)
permutation = list(np.random.permutation(m))
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((Y.shape[0],m))
# Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.
num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionning
for k in range(0, num_complete_minibatches):
mini_batch_X = shuffled_X[:, k * mini_batch_size : k * mini_batch_size + mini_batch_size]
mini_batch_Y = shuffled_Y[:, k * mini_batch_size : k * mini_batch_size + mini_batch_size]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
# Handling the end case (last mini-batch < mini_batch_size)
if m % mini_batch_size != 0:
mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size : m]
mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size : m]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches
"下載資料和標籤"
d = scio.loadmat('data1.mat')
data = d['data']
label = d['label']
print('data shape = ',data.shape)
print('label shape = ',label.shape)
"隨機打亂資料和標籤"
N = data.shape[0]
index = np.random.permutation(N)
data = data[index,:,:]
label = label[index,:]
"對資料data升維度,並且標籤 one-hot"
data = np.expand_dims(data, axis=3)
label=label-1
label = convert_to_one_hot(label,52).T
print(data.shape, label.shape)
"選取訓練樣本、測試樣本"
N = data.shape[0]
num_train = round(N*0.9)
num_test = N-num_train
X_train = data[0:num_train,:,:,:]
Y_train = label[0:num_train,:]
X_test = data[num_train:N,:,:,:]
Y_test = label[num_train:N,:]
print(" ")
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
data shape = (11322, 16, 10)
label shape = (11322, 1)
(11322, 16, 10, 1) (11322, 52)
number of training examples = 10190
number of test examples = 1132
X_train shape: (10190, 16, 10, 1)
Y_train shape: (10190, 52)
X_test shape: (1132, 16, 10, 1)
Y_test shape: (1132, 52)
def CNN_semg(input_shape=(16,10,1), classes=52):
X_input = Input(input_shape)
"block 1"
"32 filters, a row of the length of number of electrodes, ReLU"
X = Conv2D(filters=32, kernel_size=(1,10), strides=(1,1),padding='same', name='conv1')(X_input)
X = Activation('relu', name='relu1')(X)
"block 2"
"32 filters 3*3, ReLU, average pool 3*3"
X = Conv2D(filters=32, kernel_size=(3,3), strides=(1,1),padding='same', name='conv2')(X)
X = Activation('relu', name='relu2')(X)
X = AveragePooling2D((3,3), strides=(2,2), name='pool1')(X)
"block 3"
"64 filters 5*5, ReLu, average pool 3*3"
X = Conv2D(filters=64, kernel_size=(5,5), strides=(1,1),padding='same', name='conv3')(X)
X = Activation('relu', name='relu3')(X)
X = AveragePooling2D((3,3), strides=(1,1), name='pool2')(X)
"block 4"
"64 filters 5*1, ReLU"
X = Conv2D(filters=64, kernel_size=(5,1), strides=(1,1),padding='same', name='conv4')(X)
X = Activation('relu', name='relu4')(X)
"block 5"
"filters 1*1, softmax loss"
#X = Conv2D(filters=32, kernel_size=(1,1), strides=(1,1),padding='same', name='conv5')(X)
X = Flatten(name='flatten')(X)
#X = Dense(256, activation='relu', name='fc1')(X)
X = Dense(classes, activation='softmax', name='fc2')(X)
model = Model(inputs=X_input, outputs=X, name='CNN_semg')
return model
model = CNN_semg(input_shape = (16, 10, 1), classes = 52)
model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])
model.fit(X_train, Y_train, epochs=100, batch_size=64)
preds_train = model.evaluate(X_train, Y_train)
print("Train Loss = " + str(preds_train[0]))
print("Train Accuracy = " + str(preds_train[1]))
preds_test = model.evaluate(X_test, Y_test)
print("Test Loss = " + str(preds_test[0]))
print("Test Accuracy = " + str(preds_test[1]))Train Loss = 0.201551189249
Train Accuracy = 0.931207065716
Test Loss = 1.70914583493
Test Accuracy = 0.699646642899
"列印模型圖層細節"
model.summary()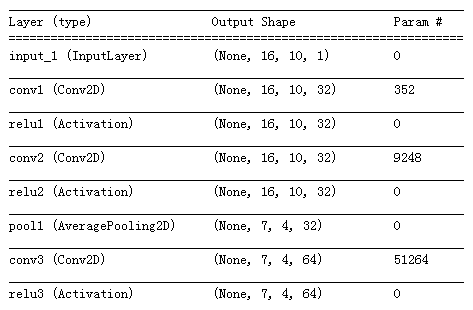
VGG16
def VGG16_semg(input_shape=(16,10,1), classes=52):
X_input = Input(input_shape)
"block 1"
X = Conv2D(filters=4, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block1_conv1')(X_input)
X = BatchNormalization(axis=3)(X)
X = Conv2D(filters=4, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block1_conv2')(X)
"block 2"
X = Conv2D(filters=8, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block2_conv1')(X)
X = BatchNormalization(axis=3)(X)
X = Conv2D(filters=8, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block2_conv2')(X)
X = BatchNormalization(axis=3)(X)
"block 3"
X = Conv2D(filters=16, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block3_conv1')(X)
X = BatchNormalization(axis=3)(X)
X = Conv2D(filters=16, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block3_conv2')(X)
X = BatchNormalization(axis=3)(X)
X = Conv2D(filters=16, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block3_conv3')(X)
X = BatchNormalization(axis=3)(X)
X = AveragePooling2D((2,2), strides=(2,2), name='block3_pool')(X)
"block 4"
X = Conv2D(filters=32, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block4_conv1')(X)
X = BatchNormalization(axis=3)(X)
X = Conv2D(filters=32, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block4_conv2')(X)
X = BatchNormalization(axis=3)(X)
X = Conv2D(filters=32, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block4_conv3')(X)
X = BatchNormalization(axis=3)(X)
"block 5"
X = Conv2D(filters=32, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block5_conv1')(X)
X = BatchNormalization(axis=3)(X)
X = Conv2D(filters=32, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block5_conv2')(X)
X = BatchNormalization(axis=3)(X)
X = Conv2D(filters=32, kernel_size=(3,3), strides=(1,1), activation='relu', padding='same', name='block5_conv3')(X)
X = BatchNormalization(axis=3)(X)
X = Flatten(name='flatten')(X)
X = Dense(256, activation='relu', name='fc1')(X)
X = Dense(classes, activation='softmax', name='fc2')(X)
model = Model(inputs=X_input, outputs=X, name='VGG16_semg')
return model
ResNet50
#殘差塊:標準塊、卷積塊
# 1、identity block
def identity_block(X, f, filters, stage, block):
# defining name basis
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
F1, F2, F3 = filters
# save the input value
X_shortcut = X
# first component of main path
X = Conv2D(filters=F1, kernel_size=(1,1), strides=(1,1), padding='valid',
name=conv_name_base+'2a', kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3, name=bn_name_base+'2a')(X)
X = Activation('relu')(X)
# second component of main path
X = Conv2D(filters=F2, kernel_size=(f,f), strides=(1,1), padding='same',
name=conv_name_base+'2b', kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3, name=bn_name_base+'2b')(X)
X = Activation('relu')(X)
# Third component of main path
X = Conv2D(filters=F3, kernel_size=(1,1), strides=(1,1), padding='valid',
name=conv_name_base+'2c', kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3, name=bn_name_base+'2c')(X)
# Final step
# Add shortcut value to main path, and pass it through a ReLU activation
X = Add()([X, X_shortcut])
X = Activation('relu')(X)
return X
# 2、convolutional block
def convolutional_block(X, f, filters, stage, block, s=2):
"""
Implementation of the identity block
Arguments:
X -- input tensor of shape (m, n_H_prev, n_W_prev, n_C_prev)
f -- integer, 主路徑中間的那個CONV的視窗形狀
filters -- python整數列表, 定義主路徑每個CONV層中的濾波器的數量
stage --整數,用於命名層,取決於他們在網路中的位置 階段
block --字串/字元,用於命名層,取決於他們在網路中的位置 塊
s -- 整數,指定滑動的大小
Returns:
X -- output of the identity block, tensor of shape (n_H, n_W, n_C)
"""
# defining name basis
conv_name_base = 'res' + str(stage) + block + '_branch'
bn_name_base = 'bn' + str(stage) + block + '_branch'
F1, F2, F3 = filters
# save the input value
X_shortcut = X
# first component of main path
X = Conv2D(filters=F1, kernel_size=(1,1), strides=(s,s), padding='valid',
name=conv_name_base+'2a', kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3, name=bn_name_base+'2a')(X)
X = Activation('relu')(X)
# second component of main path
X = Conv2D(filters=F2, kernel_size=(f,f), strides=(1,1), padding='same',
name=conv_name_base+'2b', kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3, name=bn_name_base+'2b')(X)
X = Activation('relu')(X)
# Third component of main path
X = Conv2D(filters=F3, kernel_size=(1,1), strides=(1,1), padding='valid',
name=conv_name_base+'2c', kernel_initializer=glorot_uniform(seed=0))(X)
X = BatchNormalization(axis=3, name=bn_name_base+'2c')(X)
# shortcut path
X_shortcut = Conv2D(filters=F3, kernel_size=(