IEEE 754 單精度浮點數轉換 線上計算器

十進位制小數的二進位制表示：

整數部分：除以2，取出餘數，商繼續除以2，直到得到0為止，將取出的餘數逆序

小數部分：乘以2，然後取出整數部分，將剩下的小數部分繼續乘以2，然後再取整數部分，一直取到小數部分為零為止。如果永遠不為零，則按要求保留足夠位數的小數，最後一位做0舍1入。將取出的整數順序排列。

舉例：22.8125 轉二進位制的計算過程：

整數部分：除以2，商繼續除以2，得到0為止，將餘數逆序排列。
22 / 2  11 餘0
11/2     5  餘 1
5  /2      2  餘 1
2  /2      1  餘 0
1  /2      0  餘 1
得到22的二進位制是10110

小數部分：乘以2，取整，小數部分繼續乘以2，取整，得到小數部分0為止，將整數順序排列。
0.8125x2=1.625取整1,小數部分是0.625
0.625x2=1.25取整1,小數部分是0.25
0.25x2=0.5取整0,小數部分是0.5
0.5x2=1.0取整1,小數部分是0，

得到0.8125的二進位制是0.1101

結果：十進位制22.8125等於二進位制00010110.1101

C語言和C#語言中，對於浮點型別的資料採用單精度型別（float）和雙精度型別(double)來儲存，float資料佔用32bit,double資料佔用64bit,我們在宣告一個變數float f= 2.25f的時候，是如何分配記憶體

的呢？如果胡亂分配，那世界豈不是亂套了麼，其實不論是float還是double在儲存方式上都是遵從IEEE的規範的，float遵從的是IEEE R32.24 ,而double 遵從的是R64.53。

    無論是單精度還是雙精度在儲存中都分為三個部分：

1. 符號位(Sign) : 0代表正，1代表為負
2. 指數位（Exponent）:用於儲存科學計數法中的指數資料，並且採用移位儲存
3. 尾數部分（Mantissa）：尾數部分

 其中float的儲存方式如下圖所示：

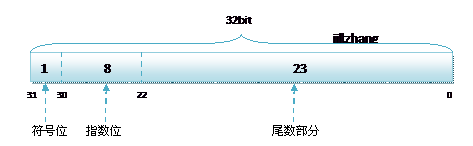
而雙精度的儲存方式為:

    R32.24和R64.53的儲存方式都是用科學計數法來儲存資料的，比如8.25用十進位制的科學計數法表示就為:8.25*

,而120.5可以表示為:1.205*,這些小學的知識就不用多說了吧。而我們傻蛋計算機根本不認識十進位制的資料，他只認識0，1，所以在計算機儲存中，首先要將上面的數更改為二進位制的科學計數法表示，8.25用二進位制表示可表示為1000.01,我靠，不會連這都不會轉換吧?那我估計要沒轍了。120.5用二進位制表示為：1110110.1用二進位制的科學計數法表示1000.01可以表示為1.0001*,1110110.1可以表示為1.1101101*,任何一個數都的科學計數法表示都為1.xxx*,尾數部分就可以表示為xxxx,第一位都是1嘛，幹嘛還要表示呀？可以將小數點前面的1省略，所以23bit的尾數部分，可以表示的精度卻變成了24bit，道理就是在這裡，那24bit能精確到小數點後幾位呢，我們知道9的二進位制表示為1001，所以4bit能精確十進位制中的1位小數點，24bit就能使float能精確到小數點後6位，而對於指數部分，因為指數可正可負，8位的指數位能表示的指數範圍就應該為:-127-128了，所以指數部分的儲存採用移位儲存，儲存的資料為元資料+127，下面就看看8.25和120.5在記憶體中真正的儲存方式。

     首先看下8.25，用二進位制的科學計數法表示為:1.0001*

按照上面的儲存方式，符號位為:0，表示為正，指數位為:3+127=130 ,位數部分為,故8.25的儲存方式如下圖所示:

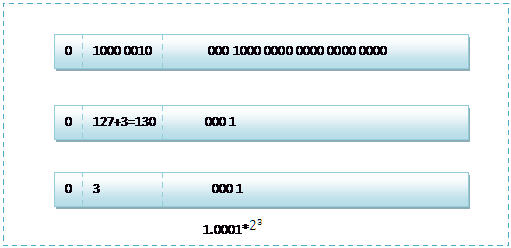
而單精度浮點數120.5的儲存方式如下圖所示:

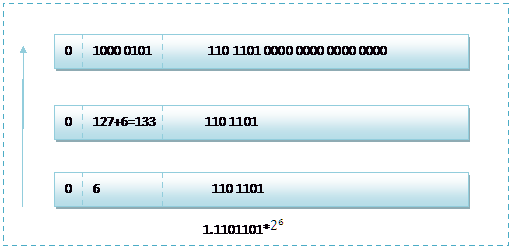
那麼如果給出記憶體中一段資料，並且告訴你是單精度儲存的話，你如何知道該資料的十進位制數值呢？其實就是對上面的反推過程，比如給出如下記憶體資料：0100001011101101000000000000，首先我們現將該資料分段，0 10000 0101 110 1101 0000 0000 0000 0000，在記憶體中的儲存就為下圖所示：

根據我們的計算方式，可以計算出，這樣一組資料表示為:1.1101101*=120.5

而雙精度浮點數的儲存和單精度的儲存大同小異，不同的是指數部分和尾數部分的位數。所以這裡不再詳細的介紹雙精度的儲存方式了，只將120.5的最後儲存方式圖給出，大家可以仔細想想為何是這樣子的

下面我就這個基礎知識點來解決一個我們的一個疑惑，請看下面一段程式，注意觀察輸出結果

            float f = 2.2f;
            double d = (double)f;
            Console.WriteLine(d.ToString("0.0000000000000"));
            f = 2.25f;
            d = (double)f;
            Console.WriteLine(d.ToString("0.0000000000000"));

可能輸出的結果讓大家疑惑不解，單精度的2.2轉換為雙精度後，精確到小數點後13位後變為了2.2000000476837，而單精度的2.25轉換為雙精度後，變為了2.2500000000000，為何2.2在轉換後的數值更改了而2.25卻沒有更改呢？很奇怪吧？其實通過上面關於兩種儲存結果的介紹，我們已經大概能找到答案。首先我們看看2.25的單精度儲存方式，很簡單 0 1000 0001 001 0000 0000 0000 0000 0000,而2.25的雙精度表示為:0 100 0000 0001 0010 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000,這樣2.25在進行強制轉換的時候，數值是不會變的，而我們再看看2.2呢，2.2用科學計數法表示應該為：將十進位制的小數轉換為二進位制的小數的方法為將小數*2，取整數部分，所以0.282=0.4，所以二進位制小數第一位為0.4的整數部分0，0.4×2=0.8，第二位為0,0.8*2=1.6,第三位為1，0.6×2 = 1.2，第四位為1，0.2*2=0.4，第五位為0，這樣永遠也不可能乘到=1.0，得到的二進位制是一個無限迴圈的排列 00110011001100110011... ,對於單精度資料來說，尾數只能表示24bit的精度，所以2.2的float儲存為:

但是這樣儲存方式，換算成十進位制的值，卻不會是2.2的，應為十進位制在轉換為二進位制的時候可能會不準確，如2.2，而double型別的資料也存在同樣的問題，所以在浮點數表示中會產生些許的誤差，在單精度轉換為雙精度的時候，也會存在誤差的問題，對於能夠用二進位制表示的十進位制資料，如2.25，這個誤差就會不存在，所以會出現上面比較奇怪的輸出結果。