The Report of the Data Lab

The Lab1 in CS:APP

毒液哥 Fudan University

CS:APP Data Lab helps develops the student’s understanding of bit
representations, two’s complement arithmetic, and IEEE floating point.

---

Preface

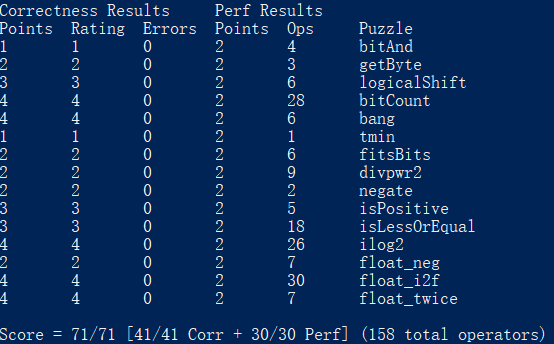
This Lab is done in the WSL(Windows Subsystem for Linux) experiment, cost about 10 hours and 158 operators are used totally.

Solution

bitAnd

int bitAnd(int x, int y) 
{
	return ~(~x | ~y);
}

For every bit in x, from De Morgan Laws we have the piece of code above.

getByte

int getByte(int x, int n) 
{
	x = x >> (n << 3);
	x = x & 0xFF;
	return x;
}

Because $1$

b y t e = 8 b i t s

1 byte = 8 bits , shift x to the right by n * 8 then & 0xFF to get the byte.

logicalShift

int logicalShift(int x, int n) 
{
	int y = x >> n;
	int Op = x >> 31;
	Op = Op << 31;
	Op = Op >> n;
	Op = Op << 1;
	x = y ^ Op;
	return x;
}

The right shift of a signed interger in C language is arithmetic shift, which fills the vacant bit-positions with the sign bit. While the arithmetic shift always fills the bit-positions with 0.

In this situation, we can simply reverse the filed bits if the sign bit of x is 1.

In the piece of code above, Op = x >> 31 << 31 distracts the sign bit of x into Op, Op >> n << 1 denotes the filled bits of x after the right shift, then Op ^ (x >> n) can set all the filled bits to 0.

bitCount

int bitCount(int x) 
{
	int y = 0x11;
	int Num;

	y = (y << 8) | 0x11;
	y = (y << 8) | 0x11;
	y = (y << 8) | 0x11;

	Num = (x & y);
	x = x >> 1;
	Num = Num + (x & y);
	x = x >> 1;
	Num = Num + (x & y);
	x = x >> 1;
	Num = Num + (x & y);
	x = x >> 1;

	y = 0;

	y = Num + (Num >> 12) + (Num >> 24);
	return (y & 0xF) + ((y >> 4) & 0xF) + ((y >> 8) & 0xF);
}

A simple way to count the number of 1s in x is that shifting every bit in x to the right most and then add it to answer after taking bitwise-and with 1, but it costs near 100 operator count.

An efficient approach is checking multiple bits in one operation. We simply construct a constant 0x11111111 using bitwise operations. By adding x to Num after taking bitwise-and with 0x11111111and right shifting it by 1, for 4 times, every nibble of Num denotes the number of 1s in the corresponding nibble, respectively. Finally we get the total answer in every nibble together in the right most nibble by right shift.

bang

int bang(int x) 
{
	x = x | (x >> 1);
	x = x | (x >> 2);
	x = x | (x >> 4);
	x = x | (x >> 8);
	x = x | (x >> 16);
	return x & 1 ^ 1;
}

In the piece of code above, we use the divide and conquer algorithm to get the or-sum of every bit into the right most bit instead of simply doing it one by one. But it isn’t the best approach if it is am optimization of brute force.

int bang(int x) 
{
	return (~x + 1 | x) >> 31 & 1 ^ 1;
}

We find that the sign bit of x and the two’s complement of x is 0 if and only if $x = 0$. Namely, the sign bit of x of the two’s compelement of x is 1 if and only if $x \ne 0$.

Hence, we have the piece of the code above.

tmin

int tmin(void) 
{
	return 1 << 31;
}

The two’s complement of 0x80000000 is 0xFFFFFFFF.

fitsBits

int fitsBits(int x, int n) 
{
	int Op = x >> 31;
	x = x ^ Op;
	x = x >> (n + ~0);
	return !x;
}

Due to the rules of two’s complement, the significant digits of a negetive integer x is the 0s in x, that is, the 1s in the reverse of x.

x = x ^ (x >> 31) reverses every bit in x if x is negetive, then we check if all the 1s are in the first $n - 1$ bits.

divpwr2

int divpwr2(int x, int n) 
{
	int Op = x + ~0;
	Op = Op >> 31;
	Op = Op & 1;
	x = ~(~x + Op);
	x = x >> n;
	x = x + Op;
	return x;
}

If x is a positive number, the value of x >> n changes when x increases if $2 ^ n | x + 1$. In this case, x >> n is an equvalence of $x / 2 ^ n$.

If x is a negetive number, the value of x >> n changes when x decreases if $2 ^ n | x$. Thus, we find that ((x - 1) >> n) + 1 is an equvalence of $x / 2 ^ n$, in this case.

In the piece of code above, Op = x >> 31 & 1 denotes the sign bit of x, ~(~x + Op) is an equavalence of $x - Op$.

But there is an exception that when $x = 0x80000000$, x - 1 changes the sign bit of x. Op = x + ~x will regard 0x80000000 as positive and we can still get the correct answer.

negate

int negate(int x) 
{
	return ~x + 1;
}

Omitted.

inPositive

int isPositive(int x) 
{
	int temp = !x;
	x = x >> 31;
	x = x & 1;
	x = x | temp;
	x = x ^ 1;
	return x;
}

x is not positive if x is negative or $x = 0$.x is negative if and only if the sign bit of x is 1.

x >> 1 & 1 checks the former situation while !x checks the latter situation.

ilog2

int ilog2(int x) 
{
	int Ans;
	int Current_Ans;

	Current_Ans = !!(x >> 16) << 4;
	Ans += Current_Ans;
	x = x >> Current_Ans;

	Current_Ans = !!(x >> 8) << 3;
	Ans += Current_Ans;
	x = x >> Current_Ans;

	Current_Ans = !!(x >> 4) << 2;
	Ans += Current_Ans;
	x = x >> Current_Ans;

	Current_Ans = !!(x >> 2) << 1;
	Ans += Current_Ans;
	x = x >> Current_Ans;

	Ans += x >> 1;
	return Ans;
}

Our objective is to find the position of 1 with the highest bit position.

Every time we use divide and conquer algorithm, divide x into two parts and check if the left part is 0. If not, we don’t care about the value of the right part, thus replace it with the left part and the answer increases by the length of the right part. Till the length of x is 2, simply execute Ans += x >> 1.

float_i2f

unsigned float_neg(unsigned uf) 
{
	if(((uf & 0x7F800000u) == 0x7F800000u) && (uf << 9u) > 0u)
		return uf;
	return uf ^ (1u << 31u);
}

Let uf be the bit-level equivalece of expression f.

f is NaN(not a number) if and only if $exp = 255 \land frac \ne 0$. If f is a number, simply reverse the sign bit of f.

Particularly, +0 and -0 is considered different in the IEEE floating-point standard.

float_i2f

unsigned float_i2f(int x) 
{
	unsigned Ans = 0;
	unsigned Now = 31;
	unsigned temp;
	unsigned temp1;
	unsigned temp2;
	unsigned X;
	if(x == 0x80000000)
		return 0xCF000000;
	if(x == 0)
		return 0;
	if(x < 0)
	{
		Ans += 0x80000000;
		X = -x;
	}
	else
		X = x;
	while((X >> Now) == 0)
		--Now;
	temp2 = Now - 24;
	temp = X >> temp2;
	temp1 = 1 << temp2;
	if(Now >= 24 && (temp & 1))
		if(X & (temp1 - 1) || (temp & 2))
			X += temp1;
	if(X >> Now + 1)
		++Now;
	if(Now > 23)
		X = X >> Now - 23;
	else
		X = X << 23 - Now;
	Ans = Ans + (X & 0x7FFFFF);
	Ans = Ans + (Now + 127 << 23);
	return Ans;
}

In the IEEE floating-point standard, the only difference between the representation of f and -f is in the sign bit. Thus, for a negative number x except 0x80000000, we do process with an unsigned interger -x.

First, we find Now, the highest bit-position with an 1 in it. Because the single precision floating-point number only has 23 significant digits, we need rounding. In general, we simply find the closest matching value. The only design decision if to determine the rounding values that are halfway between two possible results.

The default Round-to-even mode rounds the number such that the least significant digit of the result is even.

Second, we shift the 23 significant digits to the least 23 bits.

Finally, let exp be Now plus 127.

float_twice

unsigned float_twice(unsigned uf) 
{
	unsigned Frac;
	if((uf & 0x7F800000u) == 0x7F800000u)
		return uf;
	if(uf & 0x7F800000u)
		return uf + (1 << 23);
	uf += uf & 0x7FFFFF;
	return uf;
}

For the special values, return themselves.

For the normalized values, exp increases by 1.

For the denormalized values, double frac. If an overflow happens, exp exactly increases by 1 and then denotes a correct normalized value.

Summary

總結再用英文就成英語小作文大賽了

上課時金城老師講的很快，感覺三節課200頁書好，清楚地講述了IEEE標準中帶符號整數和浮點數的儲存方式。

開始做Lab之前自以為是輕車熟路，沒想到我對C語言中位運算和資料儲存方式的瞭解是如此淺薄。arithmetic shift, logical shift, two’s complement, 4 modes in rounding, 位運算子之間的優先順序以及如何用位運算實現四則運算等等，都是我之前不曾知道的。

通過通讀課本加上完成Lab中的各個函式，我對上述知識有了深刻的記憶。

最後，下次Lab一定要早點完成。