1．樹、森林到二叉樹的轉換

（1）將樹轉換為二叉樹
    　樹中每個結點最多隻有一個最左邊的孩子(長子)和一個右鄰的兄弟。按照這種關係很自然地就能將樹轉換成相應的二叉樹：
　　①在所有兄弟結點之間加一連線；
　　②對每個結點，除了保留與其長子的連線外，去掉該結點與其它孩子的連線。

【例】下面(a)圖所示的樹可轉換為(c)圖所示的二叉樹。

注意：
　    由於樹根沒有兄弟，故樹轉化為二叉樹後，二叉樹的根結點的右子樹必為空。

2）將一個森林轉換為二叉樹
 具體方法是：
　　① 將森林中的每棵樹變為二叉樹
　　② 因為轉換所得的二叉樹的根結點的右子樹均為空，故可將各二叉樹的根結點視為兄弟從左至右連在一起，就形成了一棵二叉樹。
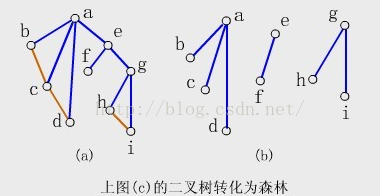
【例】下圖中，左邊包含三棵樹的森林可轉換為右邊的二叉樹。

2.二叉樹到樹、森林的轉換
　    把二叉樹轉換到樹和森林自然的方式是：若結點x是雙親y的左孩子，則把x的右孩子，右孩子的右孩子，…，都與y用連線連起來，最後去掉所有雙親到右孩子的連線。
【例】下圖的森林就是由例2中二叉樹轉換成的。 

 截圖一的題中題設為：將森林轉換為對應的的二叉樹，在二叉樹中，結點u是結點v的父結點的父結點，則在原來的森林中，u和v可能具有的關係：Ⅰ父子關係：成立；以圖為例：

Ⅱ兄弟關係：成立；以圖為例：

Ⅲu的父結點與v的父結點是兄弟關係：不成立；理由如下：

①將森林轉換為二叉樹第一步是將每棵樹轉變為二叉樹：則第一步是在所有兄弟結點之間加一連線，第二步對每個結點，除保留與長子的連線，去掉該結點與其它孩子的連線；則若u父親與v父親是兄弟關係，必連線成為父子，由此u至多為v的父親的兄弟；

②由上一步知道轉換所得的二叉樹的根結點的右子樹均空，將各二叉樹根結點視為兄弟從左至右連一起，在此有個疑問，視為兄弟，但其實沒關係的吧。即使u和v都是長子，關係仍舊如①；

③反著來，已知在二叉樹中u是v的父結點的父結點，根據森林演化成為二叉樹的條件和性質，u和v的關係可以是父子、兄弟，但無法成為u的父親與v的父親是兄弟的尷尬關係。