前言：

  在樹這一塊的資料結構中最重要的就是二叉樹，但是對於我們大部分人來說二叉樹的基礎掌握還是ok的，但是有時候我們也會忽略了樹於森林（本人就是忽略了），今天就在這裡總結總結數、森林與二叉樹的轉換

樹轉換成二叉樹

1.加線：在所有的兄弟結點之間加線 2.去線：對樹中的每一個結點，只保留它與第一個結點的連線，刪除與其他孩子結點之間的連線 3.層次調整：調整成一顆二叉樹（第一個孩子是二叉樹的左孩子，兄弟轉換過來是它的右孩子）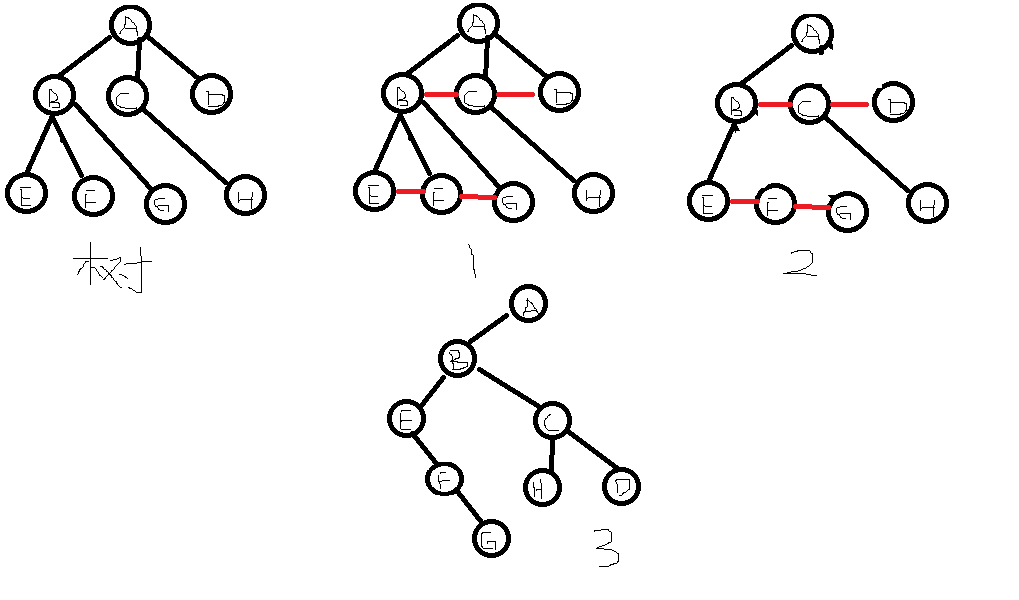

森林轉換成二叉樹

1.轉換：把每一棵樹轉換成二叉樹 2.連線：第一棵二叉樹不變，從第二棵二叉樹開始，依次將後一棵二叉樹的根節點作為前一棵二叉樹根節點的右孩子，用線連起來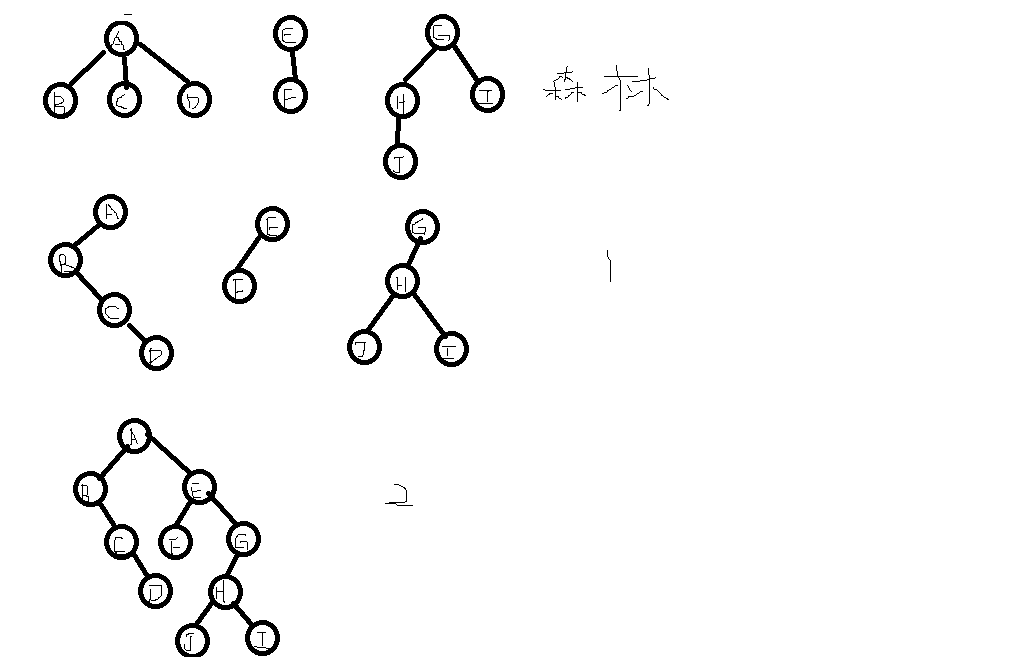

二叉樹轉換成樹

就是樹轉換成二叉樹的逆過程 1.加線：若某結點的左孩子結點存在，則將左孩子的n個右孩子結點與此結點連線在一起 2.去線：刪除二叉樹中所有結點與其右孩子之間的連線 3.層次調整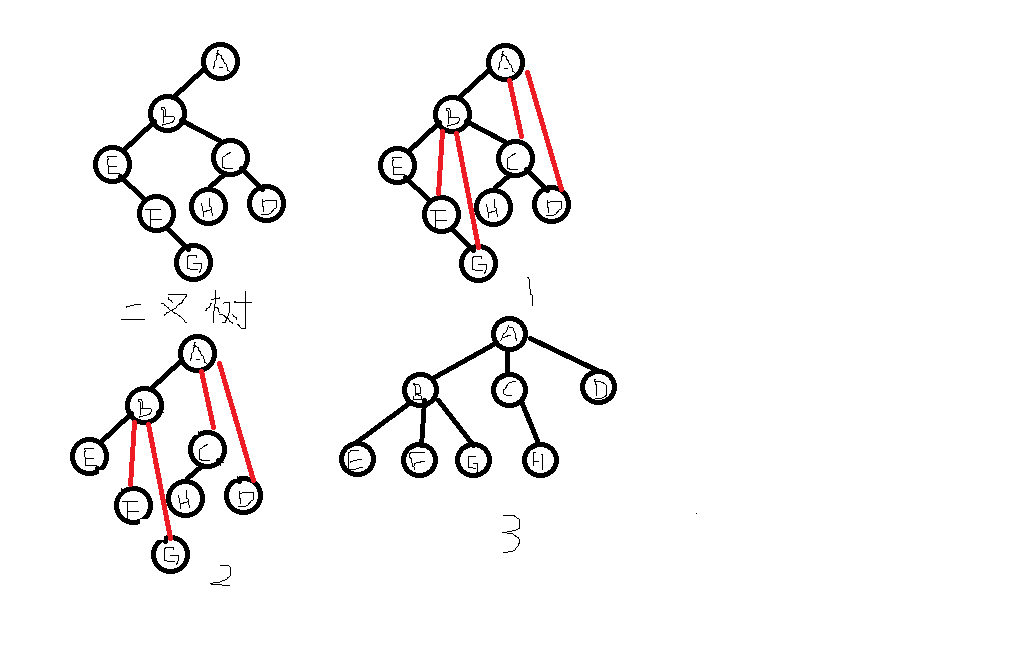
在做這幅圖的時候犯了一個錯誤：當時對比樹轉換成二叉樹圖中的1，你會發現H在右邊 當你把二叉樹轉換成圖的時候你會發現圖中2的H在左邊（當時就納悶為什麼會這樣） 原因：看了幾分鐘發現樹是沒有左右結點的（概念弄混淆了） 樹   的    遍  歷：先根遍歷：ABEFGCHD  後根遍歷：EFGBHCDA 二叉樹的遍歷： 先序遍歷    ABEFGCHD  中序遍歷：EFGBHCDA 結論：當以二叉連結串列作為樹的儲存結構，樹的先根遍歷和後根遍歷完全可以借用二叉樹的前序遍歷和中序遍歷的演算法實現

二叉樹轉換成森林

判斷二叉樹轉換成森林還是樹：二叉樹的根節點是否有右孩子，若有是森林，否則是樹 1.從根節點開始，若有右孩子，則把與右孩子結點的連線刪除，再看分離後的二叉樹，若還有右孩子連線繼續刪除，則到沒有為止 2.將分離的二叉樹轉換成樹
森林的遍歷：    前序遍歷：ABCDEFGHJI  後序遍歷：BCDAFEJHIG 二叉樹的遍歷：前序遍歷：ABCDEFGHJI  中序遍歷：BCDAFEJHIG 結論：當以二叉連結串列作為森林的儲存結構，森林的先序遍歷和後序遍歷完全可以借用二叉樹的前序遍歷和中序遍歷的演算法實現
綜上我們找到了對樹和森林這種複雜問題的簡單解決辦法