Trie樹的雙陣列實現
正文組織
1.什麼是Trie樹?
2.如何實現一個Trie樹?
3.三陣列Trie(Tripple-Array Trie)
4.雙陣列Trie(Double-Array Trie)
5.字尾壓縮
6.關鍵詞插入操作
7.關鍵詞刪除操作
8.雙輸出池分配(Double-Array Pool Allocation)
10.下載
11.其他實現
12.參考文獻
什麼是Trie樹?
Trie樹是一種數字搜尋樹。(點選檢視詳細描述)[Fredkin1960]引進了trie這個術語,是“Retrieval”的簡寫,指檢索之意。
如何實現一個Trie樹?Trie樹是一種有效的檢索方式。事實上,它也是一種確定型有限自動機(
DFA:Determine Finite Automatic,)。在Trie樹中,每一個節點都對應一個狀態,每一個標記的邊都代表一個DFA中的而一個狀態轉移關係。對Trie樹的遍歷從根節點開始,當給定一個查詢關鍵詞時,每次消耗查詢詞的一個字母,下一個節點為於當前字母相同的邊所指向的節點。當關鍵詞的所有字母消耗完或者我們到了一個葉子節點,則整個檢索過程結束。當我們走到一節點之後,發現該節點不存在於當前字母標記的邊,或者當前節點為葉子節點,而關鍵詞的字母尚未消耗完,則說明當前關鍵詞在trie樹中檢索失敗。此處要注意的是,從trie樹的根節點遍歷到葉子節點所需的時間跟資料庫的大小沒有關係,而是與查詢關鍵詞的長度成正比的。所以,trie樹的查詢通常比B-樹或者任何其他基於比較檢索的方法要快很多。它的時間複雜度與hash方法是近似的。
除了檢索效率高之外,trie樹在關鍵詞拼寫錯誤的情況下也能夠提供很好的方法來進行拼寫的檢查。例如,可以在檢索過程中跳過一些字元便可以糾正插入型別的錯誤;可以通過在不消耗字元的情況下,遍歷當前節點的所有子節點的方式便可以糾正刪除型別的錯誤;甚至我們可以噹噹前節點不存在標記為當前字元的子節點時,直接跳過當前字元,然後進入當前節點的所有子節點來達到糾正插入型別錯誤。
三陣列Trie樹通常一個DFA有一張狀態轉移表來表示,轉移表的行代表狀態機的各個狀態,列表示轉換字元。轉換表中第i行第j列的值表示在狀態i的情況下輸入字元j的時候的目標狀態。
這種表示方式能夠提供快速的遍歷,以為每一個轉移都可以有一個行號和列號進行索引。然而在空間上,這種表示形式則存在很大的浪費,因為對於trie樹,大多數的節點都只有少數的幾個分支,這邊使得轉移表中的大量的空間浪費了。
相對於轉移表表示方式,可以利用連結串列的形式來儲存每個狀態的狀態轉移關係。但是由於連結串列是一個線性訪問結構,從而導致了trie樹的檢索效率下降。
為了保證trie樹的訪問效率和空間的不浪費,便有人提出了對轉移表進行壓縮的方法來實現trie樹。
1.[Johnson1975]利用4個數組來表示DFA,在trie樹的情況下可以精簡到3個數組。這種方式下,狀態轉移表的行時以重疊的方式分配的,這樣使得那些空閒的單元能夠被其他的狀態利用。
2.[Aoe1989]提出了對3個數組的表示方式的一種改進,使得之用兩個陣列即可
雙陣列Trie樹正如 [Aho+1985] page 144-146中所講到的,DFA壓縮表示可以通過四個陣列來表示,即default,base,next以及checkt四個陣列。然而由於僅用於資訊檢索的trie樹比此法分析要簡單許多,所以default陣列其實可以省略。因此一個trie樹能夠利用三個陣列來實現。
結構
三陣列(tripple-array)結構有以下三個陣列組成:
1.base陣列:base陣列的每一個元素都對應trie樹中的一個節點。對於trie樹中的一個節點s,node[s]表示該節點在陣列next和check陣列中的起始索引,該索引表示節點s在狀態轉移表中的行號。
2.next陣列:這個陣列與check陣列協同工作。它提供給一個緩衝池以供trie樹的狀態轉移表的行所代表的的稀疏向量的空間分配。即,trie樹中的每一個節點的狀態轉移向量都會儲存於next陣列中
3.check陣列:這個陣列與next陣列協同工作。它用於標記next陣列中的元素所屬的trie樹節點。這樣便允許相鄰的兩個空間分配給不同的節點。
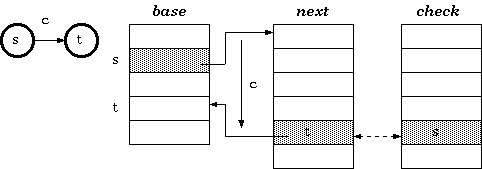
定義1:假設狀態s下,輸入字元為c時的目標狀態為t,那麼會有check[base[s] + c] = s, next[base[s] + c] = t.該關係可以用下圖表示:
遍歷
根據定義1,在給定狀態s的情況下,輸入字元為c,則下一個狀態通過如下方式獲取:
構造方式t := base[s] + c; if check[t] = s then next state := next[t] else fail endif
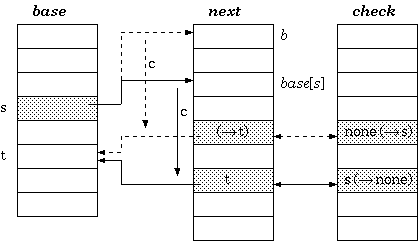
為了插入狀態s的一個新的轉移,比如輸入字元為c則轉移到狀態t,那麼要求next[base[s] + c]這個地址單元必須可用。如果該地址單元是空的,那我們可以直接插入;否則的話要麼需要移動當前單元格所有的節點或者節點s的轉移向量需要重新調整位置。實際中根據調整二者的代價來決定重新調整哪個節點的轉移向量。在找到了空閒的地址單元來儲存轉移向量之後,轉移向量必須按照如下的方式進行重新計算。假設新的存放地址從b開始,則重新分配的過程如下所示:Procedure Relocate(s : state; b : base_index) { Move base for state s to a new place beginning at b } begin foreach input character c for the state s { i.e. foreach c such that check[base[s] + c]] = s } begin check[b + c] := s; { mark owner } next[b + c] := next[base[s] + c]; { copy data } check[base[s] + c] := none { free the cell } end; base[s] := b end
利用三陣列結構實現trie樹似乎已經足夠好了,但是這種方式在實際中無法儲存在一個單一的檔案中(原句:The tripple-array structure for implementing trie appears to be well defined,but is still not practical to keep in a single file.這句覺得翻譯的不準確)。事實上next/check兩個陣列可以以整數對的形式儲存於一個數組中,但是由於base陣列並不會隨著next/check的增長而增長的,所以通常將base陣列單獨分開。
為了解決這個問題,[Aoe1989]將陣列個數減少到了兩個。在雙陣列結構中,base陣列和next數組合併為一個數組,從而該結構中只有兩個平行的陣列,即base和check陣列。
結構
在雙陣列Trie樹中,陣列中的trie樹節點是直接在base陣列和check陣列之間進行連線的,而不像三陣列的表示中的那樣通過狀態號進行連線。
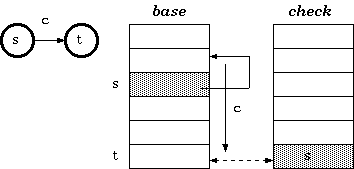
定義2:對於狀態s,如果輸入字元為c,則目標轉移狀態為t的這個轉移關係來說,base陣列和check陣列會有如下關係:check[base[s] + c] = s, base[s] + c = t.如下圖所示:
遍歷
根據定義2,當給定狀態c和輸入字元c,則下一個狀態由以下方式確定:
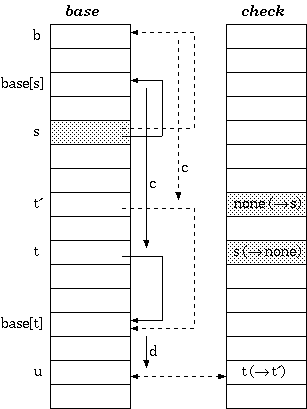
t := base[s] + c;if check[t] = s thennext state := telsefail構造endif雙陣列trie數的構建與三陣列trie樹的構建基本類似,不同點在於base陣列中空間分配:
Procedure Relocate(s : state; b : base_index){ Move base for state s to a new place beginning at b }begin
foreach input character c for the state s{ i.e. foreach c such that check[base[s] + c]] = s }begin
check[b + c] := s; { mark owner }
base[b + c] := base[base[s] + c]; { copy data }
{ the node base[s] + c is to be moved to b + c;
Hence, for any i for which check[i] = base[s] + c, update check[i] to b + c }
foreach input character d for the node base[s] + c
begin
check[base[base[s] + c] + d] := b + c
end;
check[base[s] + c] := none { free the cell }end;
base[s] := b
字尾壓縮end
[Aoe1989]在此基礎上還提出了一種儲存壓縮的策略,這種策略通過將沒有分支的字尾儲存於一個字串中,稱之為tail。這樣一來,那些沒有分支的節點訪問便簡化為字串的比較問題了。
由於雙陣列和字尾壓縮是兩個完全不同的資料結構,因此關鍵詞的插入和刪除演算法必須根據這兩個資料結構的特性做相應的調整。
關鍵詞插入
(未完待續)
相關推薦
Trie樹介紹及實現(傳統&雙陣列)
Trie樹,又叫字典樹、字首樹(Prefix Tree)、單詞查詢樹 或 鍵樹,是一種樹形結構。典型應用是用於統計和排序大量的字串(但不僅限於字串),所以經常被搜尋引擎系統用於文字詞頻統計。它的優點是最大限度地減少無謂的字串比較, 查詢效率比較高 。 Trie的核心思
Trie樹的雙陣列實現
正文組織 1.什麼是Trie樹? 2.如何實現一個Trie樹? 3.三陣列Trie(Tripple-Array Trie) 4.雙陣列Trie(Double-Array Trie) 5.字尾壓縮 6.關鍵詞插入操作 7.關鍵詞刪除操作 8.雙輸出池分配(Double-A
字典樹-大量字串字首及出現次數是否存在統計(Trie樹-java)演算法實現
前言 字典樹又稱單詞查詢樹,它是一種樹形結構,是一種雜湊樹的變種,典型應用是用於統計,儲存大量的字串(但不僅限於字串),統計以是否有以某字串最為字首的字串,有的話有多少,某字串出現了多少
Trie樹的Java實現
第一部分、Trie樹 1.1、什麼是Trie樹 Trie樹,即字典樹,又稱單詞查詢樹或鍵樹,是一種樹形結構,是一種雜湊樹的變種。典型應用是用於統計和排序大量的字串(但不僅限於字串),所以經常被搜尋引擎系統用於文字詞頻統計。它的優點是:最大限度地減少無謂的字串比較,
Trie 樹的簡單實現
Trie 樹, 又稱字首樹,是一種高校的動態儲存結構 查詢效率:O(m) m為串的長度 空間要優於BST(二叉搜尋樹),因為Trie 樹是字首複用的。 實現了插入、刪除、顯示 加了註釋,另外解構函式沒有實現,釋放樹資源的函式也沒有實現 :( #define CHA
Stars (HDU 1541)——樹狀陣列實現
StarsTime Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submission(s): 11904 Accepted Submission(
雙陣列TRIE樹原理
關鍵詞查詢策略可以被大致分為兩類,按照關鍵詞集合是否可變可以將這些演算法分為“動態方法”(允許查詢表被修改)和“靜態方法”(顯然相反)兩種。廣為人知的“動態方法”有:hashing,二叉樹,B+樹,擴充套件hashing,和trie hashing。而“靜態方法”有:完美hashing,稀疏表,以及壓縮tri
雙陣列Trie樹 (Double-array Trie) 及其應用
雙陣列Trie樹(Double-array Trie, DAT)是由三個日本人提出的一種Trie樹的高效實現 [1],兼顧了查詢效率與空間儲存。Ansj便是用DAT(雖然作者宣稱是三陣列Trie樹,但本質上還是DAT)構造詞典用作初次分詞,極大地節省了記憶體佔用。本文將簡要地介紹DAT,並實現了基於DAT的前
雙陣列trie樹的基本構造及簡單優化(DAT沒那麼複雜)
一 基本構造 Trie樹是搜尋樹的一種,來自英文單詞"Retrieval"的簡寫,可以建立有效的資料檢索組織結構,是中文匹配分詞演算法中詞典的一種常見實現。它本質上是一個確定的有限狀態自動機(DFA),每個節點代表自動機的一個狀態。在詞典中這此狀態包括“詞字首”,“已成
[轉]Trie樹優化演算法:Double Array Trie 雙陣列Trie
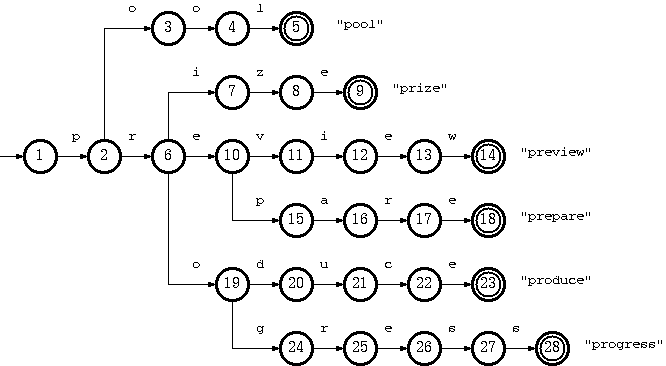
Trie邏輯結構 Trie是一種常見的資料結夠,可以實現字首匹配(hash是不行的),而且對於詞典搜尋來說也是O(1)的時間複雜度,雖然比不上Hash,但是空間會省不少。 比如下圖表示了包含“pool, prize, preview, prepare,
雙陣列字典樹(Double Array Trie)
參考文獻 1.雙陣列字典樹(DATrie)詳解及實現 2.小白詳解Trie樹 3.論文《基於雙陣列Trie樹演算法的字典改進和實現》 DAT的基本內容介紹這裡就不展開說了,從Trie過來的同學應該比較熟悉,Trie對記憶體的消耗比較大,DA
線段樹模板(陣列實現)
首先是基本定義環節 因為線段樹左子節點和右子節點在建構函式的時候比較常用 我們就把這兩個語句簡化一下; #define lson l, m, rt<<1 #define rson m+1, r, rt<<1|1 const int maxn=5008;
CH601字尾陣列【Trie樹】
內含字典樹建立及查詢模板 1601 字首統計 0x10「基本資料結構」例題 描述 給定N個字串S1,S2...SN,接下來進行M次詢問,每次詢問給定一個字串T,求S1~SN中有多少個字串是T的字首。輸入字串的總長度不超過10^6,僅包含小寫字母。 輸入格式 第一行兩個整數N,M。接下來N行
深入雙陣列Trie(Double-Array Trie)
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
樹狀陣列的原理及實現
對於樹狀陣列,它的查詢和修改的時間複雜度都是log(n),空間複雜度則為O(n),這是因為樹狀陣列通過將線性結構轉化成樹狀結構,從而進行跳躍式掃描。通常使用在高效的計算數列的字首和,區間和。 附上一張圖便於理解 其中a陣列就是原陣列,c陣列則是樹狀陣列,可以發現
[Trie樹] 統計英文文字中單詞出現的個數 - C語言實現 - 考慮數字、英文
【英文文字】 However, after reaching the shore there are plenty of challenges waiting for him."The biggest challenge now is learning to walk agai
LeetCode 208. Implement Trie (Prefix Tree) (實現Trie樹)
原題 Implement a trie with insert, search, and startsWith methods. Example: Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"
利用trie樹實現字首輸入提示(python)
程式碼來自https://github.com/wklken/suggestion/blob/master/easymap/suggest.py 還實現了快取功能,搜尋某個字首超過一定次數時,進行快取,減少搜尋時間:將詞字尾部分儲存在節點 使用了詞頻資訊,可以對返回的列表進行排序 使用dict實現tri
字典樹(Trie樹)模板 陣列表示 + 連結串列表示
陣列模擬,缺點是並不知道要開多大,可能會出現陣列開小導致wrong answer。 對應題目:hdu 1251 #include <iostream> #include <cstdio> #include <cstring> #de
樹狀陣列套trie 模板
求區間排名,第K大,單點修改,區間前驅,區間後驅。 時間複雜度O(logn^3) #include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<algorit