題目背景

滾粗了的HansBug在收拾舊語文書，然而他發現了什麼奇妙的東西。

題目描述

蒟蒻HansBug在一本語文書裡面發現了一本答案，然而他卻明明記得這書應該還包含一份練習題。然而出現在他眼前的書多得數不勝數，其中有書，有答案，有練習冊。已知一個完整的書冊均應該包含且僅包含一本書、一本練習冊和一份答案，然而現在全都亂做了一團。許多書上面的字跡都已經模糊了，然而HansBug還是可以大致判斷這是一本書還是練習冊或答案，並且能夠大致知道一本書和答案以及一本書和練習冊的對應關係（即僅僅知道某書和某答案、某書和某練習冊有可能相對應，除此以外的均不可能對應）。既然如此，HansBug想知道在這樣的情況下，最多可能同時組合成多少個完整的書冊。

輸入輸出格式

第一行包含三個正整數N1、N2、N3，分別表示書的個數、練習冊的個數和答案的個數。

第二行包含一個正整數M1，表示書和練習冊可能的對應關係個數。

接下來M1行每行包含兩個正整數x、y，表示第x本書和第y本練習冊可能對應。（1<=x<=N1，1<=y<=N2）

第M1+3行包含一個正整數M2，表述書和答案可能的對應關係個數。

接下來M2行每行包含兩個正整數x、y，表示第x本書和第y本答案可能對應。（1<=x<=N1，1<=y<=N3）

輸出包含一個正整數，表示最多可能組成完整書冊的數目。

輸入輸出樣例

5 3 4
5
4 3
2 2
5 2
5 1
5 3
5
1 3
3 1
2 2
3 3
4 3

2

說明

樣例說明：

如題，N1=5，N2=3，N3=4，表示書有5本、練習冊有3本、答案有4本。

M1=5，表示書和練習冊共有5個可能的對應關係，分別為：書4和練習冊3、書2和練習冊2、書5和練習冊2、書5和練習冊1以及書5和練習冊3。

M2=5，表示數和答案共有5個可能的對應關係，分別為：書1和答案3、書3和答案1、書2和答案2、書3和答案3以及書4和答案3。

所以，以上情況的話最多可以同時配成兩個書冊，分別為：書2+練習冊2+答案2、書4+練習冊3+答案3。

資料規模：

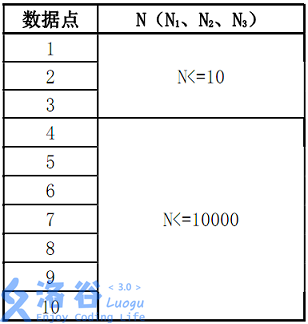
對於資料點1, 2, 3，M1，M2<= 20

對於資料點4~10，M1，M2 <= 20000

把書拆點，然後跑一遍最大流

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize(2)
using namespace std;
#define maxn 2000005
#define inf 0x7fffffff
//#define INF 1e18
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
typedef pair<int, int> pii;
inline ll rd() {
	ll x = 0;
	char c = getchar();
	bool f = false;
	while (!isdigit(c)) {
		if (c == '-') f = true;
		c = getchar();
	}
	while (isdigit(c)) {
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return f ? -x : x;
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
int sqr(int x) { return x * x; }


/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0; return a;
	}
	ans = exgcd(b, a%b, x, y);
	ll t = x; x = y; y = t - a / b * y;
	return ans;
}
*/
int n, m;
int st, ed;
struct node {
	int u, v, nxt, w;
}edge[maxn];
int head[maxn];
int tot;
void addedge(int u, int v, int w) {
	edge[tot].u = u; edge[tot].v = v; edge[tot].nxt = head[u];
	edge[tot].w = w; head[u] = tot++;
}
int rk[maxn];
int bfs() {
	queue<int>q; ms(rk); rk[st] = 1; q.push(st);
	while (!q.empty()) {
		int tmp = q.front(); q.pop();
		for (int i = head[tmp]; i != -1; i = edge[i].nxt) {
			int to = edge[i].v;
			if (rk[to] || edge[i].w <= 0)continue;
			rk[to] = rk[tmp] + 1; q.push(to);
		}
	}
	return rk[ed];
}
int dfs(int u, int flow) {
	if (u == ed)return flow;
	int add = 0;
	for (int i = head[u]; i != -1 && add < flow; i = edge[i].nxt) {
		int v = edge[i].v;
		if (rk[v] != rk[u] + 1 || !edge[i].w)continue;
		int tmpadd = dfs(v, min(edge[i].w, flow - add));
		if (!tmpadd) { rk[v] = -1; continue; }
		edge[i].w -= tmpadd; edge[i ^ 1].w += tmpadd; add += tmpadd;
	}
	return add;
}
int ans;
void dinic() {
	while (bfs())ans += dfs(st, inf);
}

int N1, N2, N3;

int main() {
	//ios::sync_with_stdio(0);
	memset(head, -1, sizeof(head));
	rdint(N1); rdint(N2); rdint(N3);
	int m1; rdint(m1);
	st = 2 * N1 + N2 + N3 + 3; ed = st + 1;
	while (m1--) {
		int x, y;
		rdint(x); rdint(y);
		addedge(y, x + N2, 1); addedge(x + N2, y, 0);
	//	addedge(st, y, 1); addedge(y, st, 0);
	}
	int m2; rdint(m2);
	while (m2--) {
		int x, y; rdint(x); rdint(y);
		addedge(x + N1 + N2, y + N1 * 2 + N2, 1); addedge(y + 2 * N1 + N2, x + N1 + N2, 0);
	//	addedge(y + 2 * N1 + N2, ed, 1); addedge(ed, 2 * N1 + N2 + y, 0);
	}
	for (int i = 1; i <= N1; i++) {
		addedge(i + N2, i + N2 + N1, 1); addedge(i + N2 + N1, i + N2, 0);
	}
	for (int i = 1; i <= N2; i++)addedge(st, i, 1), addedge(i, st, 0);
	for (int i = 1; i <= N3; i++)addedge(i + 2 * N1 + N2, ed, 1), addedge(ed, i + 2 * N1 + N2, 0);
	dinic();
	cout << ans << endl;
	return 0;
}

dinic；