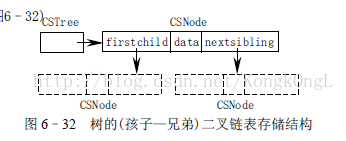
樹的儲存結構（樹的二叉連結串列(孩子—兄弟)）

阿新 • • 發佈：2019-01-14

// c6-5.h 樹的二叉連結串列(孩子—兄弟)儲存結構(見圖6.32)
typedef struct CSNode
{
	TElemType data;
	CSNode *firstchild,*nextsibling;
}CSNode,*CSTree;

一棵樹無論有多少叉，它最多有一個長子和一個排序恰在其下的兄弟。根據這樣的定
義，則每個結點的結構就都統一到了二叉連結串列結構上。這樣有利於對結點進行操作。圖
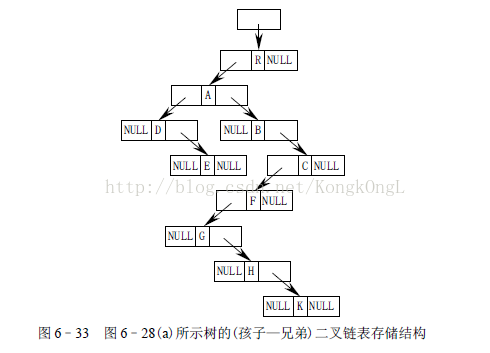
633 是圖628(a)所示之樹的二叉連結串列(孩子—兄弟)儲存結構。

// func6-2.cpp bo6-5.cpp和algo7-1.cpp呼叫
void PreOrderTraverse(CSTree T,void(*Visit)(TElemType))
{ // 先根遍歷孩子—兄弟二叉連結串列結構的樹T
	if(T)
	{
		Visit(T->data); // 先訪問根結點
		PreOrderTraverse(T->firstchild,Visit); // 再先根遍歷長子子樹
		PreOrderTraverse(T->nextsibling,Visit); // 最後先根遍歷下一個兄弟子樹
	}
}

// bo6-5.cpp 樹的二叉連結串列(孩子—兄弟)儲存(儲存結構由c6-5.h定義)的基本操作(17個)
#define ClearTree DestroyTree // 二者操作相同
#include"func6-2.cpp" // 包括PreOrderTraverse()
void InitTree(CSTree &T)
{ // 操作結果：構造空樹T
	T=NULL;
}
void DestroyTree(CSTree &T)
{ // 初始條件：樹T存在。操作結果：銷燬樹T
	if(T)
	{
		if(T->firstchild) // T有長子
			DestroyTree(T->firstchild); // 銷燬T的長子為根結點的子樹
		if(T->nextsibling) // T有下一個兄弟
			DestroyTree(T->nextsibling); // 銷燬T的下一個兄弟為根結點的子樹
		free(T); // 釋放根結點
		T=NULL;
	}
}
typedef CSTree QElemType; // 定義佇列元素型別
#include"c3-2.h" // 定義LinkQueue型別(鏈佇列)
#include"bo3-2.cpp" // LinkQueue型別的基本操作
void CreateTree(CSTree &T)
{ // 構造樹T
	char c[20]; // 臨時存放孩子結點(設不超過20個)的值
	CSTree p,p1;
	LinkQueue q;
	int i,l;
	InitQueue(q);
	printf("請輸入根結點(字元型,空格為空): ");
	scanf("%c%*c",&c[0]);
	if(c[0]!=Nil) // 非空樹
	{
		T=(CSTree)malloc(sizeof(CSNode)); // 建立根結點
		T->data=c[0];
		T->nextsibling=NULL;
		EnQueue(q,T); // 入隊根結點的指標
		while(!QueueEmpty(q)) // 隊不空
		{
			DeQueue(q,p); // 出隊一個結點的指標
			printf("請按長幼順序輸入結點%c的所有孩子: ",p->data);
			gets(c);
			l=strlen(c);
			if(l>0) // 有孩子
			{
				p1=p->firstchild=(CSTree)malloc(sizeof(CSNode)); // 建立長子結點
				p1->data=c[0];
				for(i=1;i<l;i++)
				{
					p1->nextsibling=(CSTree)malloc(sizeof(CSNode)); // 建立下一個兄弟結點
					EnQueue(q,p1); // 入隊上一個結點
					p1=p1->nextsibling;
					p1->data=c[i];
				}
				p1->nextsibling=NULL;
				EnQueue(q,p1); // 入隊最後一個結點
			}
			else
				p->firstchild=NULL; // 長子指標為空
		}
	}
	else
		T=NULL; // 空樹
}
Status TreeEmpty(CSTree T)
{ // 初始條件：樹T存在。操作結果：若T為空樹，則返回TURE；否則返回FALSE
	if(T) // T不空
		return FALSE;
	else
		return TRUE;
}
int TreeDepth(CSTree T)
{ // 初始條件：樹T存在。操作結果：返回T的深度
	CSTree p;
	int depth,max=0;
	if(!T) // 樹空
		return 0;
	if(!T->firstchild) // 樹無長子
		return 1;
	for(p=T->firstchild;p;p=p->nextsibling)
	{ // 求子樹深度的最大值
		depth=TreeDepth(p);
		if(depth>max)
			max=depth;
	}
	return max+1; // 樹的深度=子樹深度最大值+1
}
TElemType Value(CSTree p)
{ // 返回p所指結點的值
	return p->data;
}
TElemType Root(CSTree T)
{ // 初始條件：樹T存在。操作結果：返回T的根
	if(T)
		return Value(T);
	else
		return Nil;
}
CSTree Point(CSTree T,TElemType s)
{ // 返回二叉連結串列(孩子—兄弟)樹T中指向元素值為s的結點的指標。另加
	LinkQueue q;
	QElemType a;
	if(T) // 非空樹
	{
		InitQueue(q); // 初始化佇列
		EnQueue(q,T); // 根結點入隊
		while(!QueueEmpty(q)) // 隊不空
		{
			DeQueue(q,a); // 出隊,佇列元素賦給a
			if(a->data==s)
				return a;
			if(a->firstchild) // 有長子
				EnQueue(q,a->firstchild); // 入隊長子
			if(a->nextsibling) // 有下一個兄弟
				EnQueue(q,a->nextsibling); // 入隊下一個兄弟
		}
	}
	return NULL;
}
Status Assign(CSTree &T,TElemType cur_e,TElemType value)
{ // 初始條件：樹T存在，cur_e是樹T中結點的值。操作結果：改cur_e為value
	CSTree p;
	if(T) // 非空樹
	{
		p=Point(T,cur_e); // p為cur_e的指標
		if(p) // 找到cur_e
		{
			p->data=value; // 賦新值
			return OK;
		}
	}
	return ERROR ; // 樹空或沒找到
}
TElemType Parent(CSTree T,TElemType cur_e)
{ // 初始條件：樹T存在，cur_e是T中某個結點
	// 操作結果：若cur_e是T的非根結點，則返回它的雙親；否則函式值為“空”
	CSTree p,t;
	LinkQueue q;
	InitQueue(q);
	if(T) // 樹非空
	{
		if(Value(T)==cur_e) // 根結點值為cur_e
			return Nil;
		EnQueue(q,T); // 根結點入隊
		while(!QueueEmpty(q))
		{
			DeQueue(q,p);
			if(p->firstchild) // p有長子
			{
				if(p->firstchild->data==cur_e) // 長子為cur_e
					return Value(p); // 返回雙親
				t=p; // 雙親指標賦給t
				p=p->firstchild; // p指向長子
				EnQueue(q,p); // 入隊長子
				while(p->nextsibling) // 有下一個兄弟
				{
					p=p->nextsibling; // p指向下一個兄弟
					if(Value(p)==cur_e) // 下一個兄弟為cur_e
						return Value(t); // 返回雙親
					EnQueue(q,p); // 入隊下一個兄弟
				}
			}
		}
	}
	return Nil; // 樹空或沒找到cur_e
}
TElemType LeftChild(CSTree T,TElemType cur_e)
{ // 初始條件：樹T存在，cur_e是T中某個結點
	// 操作結果：若cur_e是T的非葉子結點，則返回它的最左孩子；否則返回“空”
	CSTree f;
	f=Point(T,cur_e); // f指向結點cur_e
	if(f&&f->firstchild) // 找到結點cur_e且結點cur_e有長子
		return f->firstchild->data;
	else
		return Nil;
}
TElemType RightSibling(CSTree T,TElemType cur_e)
{ // 初始條件：樹T存在，cur_e是T中某個結點
	// 操作結果：若cur_e有右兄弟，則返回它的右兄弟；否則返回“空”
	CSTree f;
	f=Point(T,cur_e); // f指向結點cur_e
	if(f&&f->nextsibling) // 找到結點cur_e且結點cur_e有右兄弟
		return f->nextsibling->data;
	else
		return Nil; // 樹空
}
Status InsertChild(CSTree &T,CSTree p,int i,CSTree c)
{ // 初始條件：樹T存在，p指向T中某個結點，1≤i≤p所指結點的度+1，非空樹c與T不相交
	// 操作結果：插入c為T中p結點的第i棵子樹
	// 因為p所指結點的地址不會改變，故p不需是引用型別
	int j;
	if(T) // T不空
	{
		if(i==1) // 插入c為p的長子
		{
			c->nextsibling=p->firstchild; // p的原長子現是c的下一個兄弟(c本無兄弟)
			p->firstchild=c;
		}
		else // 找插入點
		{
			p=p->firstchild; // 指向p的長子
			j=2;
			while(p&&j<i)
			{
				p=p->nextsibling;
				j++;
			}
			if(j==i) // 找到插入位置
			{
				c->nextsibling=p->nextsibling;
				p->nextsibling=c;
			}
			else // p原有孩子數小於i-1
				return ERROR;
		}
		return OK;
	}
	else // T空
		return ERROR;
}
Status DeleteChild(CSTree &T,CSTree p,int i)
{ // 初始條件：樹T存在，p指向T中某個結點，1≤i≤p所指結點的度
	// 操作結果：刪除T中p所指結點的第i棵子樹
	// 因為p所指結點的地址不會改變，故p不需是引用型別
	CSTree b;
	int j;
	if(T) // T不空
	{
		if(i==1) // 刪除長子
		{
			b=p->firstchild;
			p->firstchild=b->nextsibling; // p的原次子現是長子
			b->nextsibling=NULL;
			DestroyTree(b);
		}
		else // 刪除非長子
		{
			p=p->firstchild; // p指向長子
			j=2;
			while(p&&j<i)
			{
				p=p->nextsibling;
				j++;
			}
			if(j==i) // 找到第i棵子樹
			{
				b=p->nextsibling;
				p->nextsibling=b->nextsibling;
				b->nextsibling=NULL;
				DestroyTree(b);
			}
			else // p原有孩子數小於i
				return ERROR;
		}
		return OK;
	}
	else
		return ERROR;
}
void PostOrderTraverse(CSTree T,void(*Visit)(TElemType))
{ // 後根遍歷孩子—兄弟二叉連結串列結構的樹T
	CSTree p;
	if(T)
	{
		if(T->firstchild) // 有長子
		{
			PostOrderTraverse(T->firstchild,Visit); // 後根遍歷長子子樹
			p=T->firstchild->nextsibling; // p指向長子的下一個兄弟
			while(p)
			{
				PostOrderTraverse(p,Visit); // 後根遍歷下一個兄弟子樹
				p=p->nextsibling; // p指向再下一個兄弟
			}
		}
		Visit(Value(T)); // 最後訪問根結點
	}
}
void LevelOrderTraverse(CSTree T,void(*Visit)(TElemType))
{ // 層序遍歷孩子—兄弟二叉連結串列結構的樹T
	CSTree p;
	LinkQueue q;
	InitQueue(q);
	if(T)
	{
		Visit(Value(T)); // 先訪問根結點
		EnQueue(q,T); // 入隊根結點的指標
		while(!QueueEmpty(q)) // 隊不空
		{
			DeQueue(q,p); // 出隊一個結點的指標
			if(p->firstchild) // 有長子
			{
				p=p->firstchild;
				Visit(Value(p)); // 訪問長子結點
				EnQueue(q,p); // 入隊長子結點的指標
				while(p->nextsibling) // 有下一個兄弟
				{
					p=p->nextsibling;
					Visit(Value(p)); // 訪問下一個兄弟
					EnQueue(q,p); // 入隊兄弟結點的指標
				}
			}
		}
	}
}

// main6-5.cpp 檢驗bo6-5.cpp的主程式
#include"c1.h"
typedef char TElemType;
TElemType Nil=' '; // 以空格符為空
#include"c6-5.h"
#include"bo6-5.cpp"
void vi(TElemType c)
{
	printf("%c ",c);
}
void main()
{
	int i;
	CSTree T,p,q;
	TElemType e,e1;
	InitTree(T);
	printf("構造空樹後,樹空否? %d(1:是0:否) 樹根為%c 樹的深度為%d\n",TreeEmpty(T),Root(T),
		TreeDepth(T));
	CreateTree(T);
	printf("構造樹T後,樹空否? %d(1:是0:否) 樹根為%c 樹的深度為%d\n",TreeEmpty(T),Root(T),
		TreeDepth(T));
	printf("先根遍歷樹T:\n");
	PreOrderTraverse(T,vi);
	printf("\n請輸入待修改的結點的值新值: ");
	scanf("%c%*c%c%*c",&e,&e1);
	Assign(T,e,e1);
	printf("後根遍歷修改後的樹T:\n");
	PostOrderTraverse(T,vi);
	printf("\n%c的雙親是%c,長子是%c,下一個兄弟是%c\n",e1,Parent(T,e1),LeftChild(T,e1),
		RightSibling(T,e1));
	printf("建立樹p:\n");
	InitTree(p);
	CreateTree(p);
	printf("層序遍歷樹p:\n");
	LevelOrderTraverse(p,vi);
	printf("\n將樹p插到樹T中，請輸入T中p的雙親結點子樹序號: ");
	scanf("%c%d%*c",&e,&i);
	q=Point(T,e);
	InsertChild(T,q,i,p);
	printf("層序遍歷樹T:\n");
	LevelOrderTraverse(T,vi);
	printf("\n刪除樹T中結點e的第i棵子樹，請輸入e i: ");
	scanf("%c%d",&e,&i);
	q=Point(T,e);
	DeleteChild(T,q,i);
	printf("層序遍歷樹T:\n",e,i);
	LevelOrderTraverse(T,vi);
	printf("\n");
	DestroyTree(T);
}

程式碼的執行結果：

構造空樹後,樹空否? 1(1:是0:否) 樹根為樹的深度為0
請輸入根結點(字元型,空格為空): R
請按長幼順序輸入結點R的所有孩子: ABC
請按長幼順序輸入結點A的所有孩子: DE
請按長幼順序輸入結點B的所有孩子:
請按長幼順序輸入結點C的所有孩子: F
請按長幼順序輸入結點D的所有孩子:
請按長幼順序輸入結點E的所有孩子:
請按長幼順序輸入結點F的所有孩子: GHK
請按長幼順序輸入結點G的所有孩子:
請按長幼順序輸入結點H的所有孩子:
請按長幼順序輸入結點K的所有孩子:
構造樹T後,樹空否? 0(1:是0:否) 樹根為R 樹的深度為4
先根遍歷樹T:(見圖628(a))
R A D E B C F G H K
請輸入待修改的結點的值新值: D d
後根遍歷修改後的樹T:
d E A B G H K F C R
d的雙親是A,長子是,下一個兄弟是E
建立樹p:
請輸入根結點(字元型,空格為空): f
請按長幼順序輸入結點f的所有孩子: ghk
請按長幼順序輸入結點g的所有孩子:
請按長幼順序輸入結點h的所有孩子:
請按長幼順序輸入結點k的所有孩子:
層序遍歷樹p:(見圖629)
f g h k
將樹p插到樹T中，請輸入T中p的雙親結點子樹序號: R 3
層序遍歷樹T:(見圖630)
R A B f C d E g h k F G H K
刪除樹T中結點e的第i棵子樹，請輸入e i: C 1
層序遍歷樹T:(見圖631)

R A B f C d E g h k

樹的儲存結構（樹的二叉連結串列(孩子—兄弟)）

樹的儲存結構（樹的二叉連結串列(孩子—兄弟)）

二叉連結串列的儲存結構和基本操作（各種遍歷、求樹深度、求樹葉個數）

二叉樹採用二叉連結串列儲存，複製二叉樹的演算法（樹的應用）

以雙向線索連結串列為儲存結構的線索二叉樹遍歷

NOJ-建立二叉樹的二叉連結串列儲存結構-西工大資料結構

二叉樹的二叉連結串列儲存結構構建以及先序遍歷

資料結構樹筆記-5 線索二叉樹以及線索二叉連結串列

二叉樹的二叉連結串列儲存

用二叉連結串列儲存的二叉樹進行先序、中序和後序遍歷的演算法

[二叉樹] △ 6.65 已經前序序列、中序序列建立二叉樹（二叉連結串列）

[資料結構]二叉樹之二叉連結串列的類模板實現

C#實現二叉樹--二叉連結串列結構

c語言實現二叉樹（二叉連結串列）非遞迴後序遍歷

“樹”據結構一：二叉搜尋樹（Binary Search Tree, BST）

二叉連結串列（鏈式二叉樹）的非遞迴建立

c語言實現二叉樹的基本操作--二叉連結串列儲存

資料結構C語言——用二叉連結串列示二叉樹

擴充套件的先序遍歷序列建立以二叉連結串列方式儲存的二叉樹，後序遍歷

二叉樹基本概念（滿二叉樹、完全二叉樹，滿二叉樹，二叉樹的遍歷）

樹的儲存結構（樹的二叉連結串列(孩子—兄弟)）

相關推薦