python實現斐波那契數列 用遞迴實現求第N個菲波那切數列
斐波那契數列即著名的兔子數列:1、1、2、3、5、8、13、21、34、……
數列特點:該數列從第三項開始,每個數的值為其前兩個數之和,用python實現起來很簡單:
a=0
b=1
while b < 1000:
print(b)
a, b = b, a+b輸出結果:
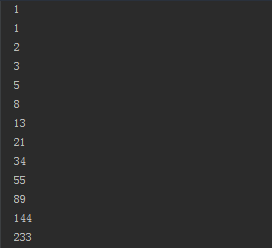
這裡 a, b = b, a+b 右邊的表示式會在賦值變動之前執行,即先執行右邊,比如第一次迴圈得到b-->1,a+b --> 0+1 然後再執行賦值 a,b =1,0+1,所以執行完這條後a=1,b=1
a=0 b=1 while b < 1000: print(b,end=',')#end 可以將print輸出到同一行並以 ,號結尾 a, b = b, a+b
輸出結果:

遞迴方式實現斐波那契數列 前n項:
# 遞迴方式實現 生成前20項
lis =[]
for i in range(20):
if i ==0 or i ==1:#第1,2項 都為1
lis.append(1)
else:
lis.append(lis[i-2]+lis[i-1])#從第3項開始每項值為前兩項值之和
print(lis)或者
def func(n): # 給遞迴一個出口 第一位和第二位都是1 if n == 1 or n == 2: return 1 else: # 從第三位開始 返回上一個數加上上一個數 return func(n-1) + func(n-2) # func(5) + func(4) # func(4)+func(3) + func(3) + func(2) # func(3)+func(2) + func(2)+func(1) + func(2)+func(1) + 1 # func(2)+func(1) + 1 + 1+1 + 1+1 + 1 # 1+1 + 1 + 1+1 +1+1 + 1 = 8 res = func(20) print(res)
執行結果

相關推薦
python實現斐波那契數列 用遞迴實現求第N個菲波那切數列
斐波那契數列即著名的兔子數列:1、1、2、3、5、8、13、21、34、…… 數列特點:該數列從第三項開始,每個數的值為其前兩個數之和,用python實現起來很簡單: a=0 b=1 while b < 1000: print(b) a, b = b, a+b
python實現斐波那契數列 用遞迴實現求第N個菲波那切數列
斐波那契數列即著名的兔子數列:1、1、2、3、5、8、13、21、34、…… 數列特點:該數列從第三項開始,每個數的值為其前兩個數之和,用python實現起來很簡單: a=0 b=1 while b < 1000: print(b) a, b = b
求第n個斐波那契數(用遞迴的形式)
#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> int Fib(int n) { if (n == 1 || n == 2) // |按位或,||邏輯或 { retur
還在用遞迴實現斐波那契數列,面試官一定會鄙視你到死
斐波那契數列指的是這樣一個數列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368...... &nb
斐波那契數列用遞迴還是迴圈好
/** * */ /** * @author jueying: * @version 建立時間:2018-11-15 下午10:21:26 * 類說明 */ /** * @author jueying * */ public class Test12
用遞迴演算法求斐波那契數列的第N項值
#include <stdio.h> long fun(int g) { switch(g) { case 0: return 0; case 1: return 0; case 2: return 1; } return (fun(
實現求第n個斐波那契數
斐波那契數列:指的是這樣一個數列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368..這個數列從第3項開始,每一項都等於前兩項之和 求第n個斐
求第n個斐波那契數(分別用遞迴和非遞迴兩種方法求解)
斐波那契數列指的是這樣一個數列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55……這個數列從第3項開始,每一項都等於前兩項之和。 這裡分別用遞迴和非遞迴的方法實現: 遞迴 #define _CRT_SECURE_NO_WARNINGS 1 #include&l
遞迴和非遞迴分別實現求第n個斐波那契數。
//非遞迴 int main() { int a = 0; int b = 1; int c = 0; int i = 0; int n = 0; printf("請輸入數字n(n>2)求第n個斐波那契數:"); scanf("%d",&n); for(i =
演算法之斐波那契數列如何求第n個值與求前n項和?(Java)
斐波那契數列 指的是這樣一個數列:1、1、2、3、5、8、13、21、34、……在數學上,斐波納契數列以如下被以遞推的方法定義:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*)。 1.題目 1.1.求斐波那契數
1.遞迴和非遞迴分別實現求第n個斐波那契數。 遞迴與非遞迴的典型題型
1.遞迴和非遞迴分別實現求第n個斐波那契數。 2.編寫一個函式實現n^k,使用遞迴實現 寫一個遞迴函式DigitSum(n),輸入一個非負整數,返回組成它的數字之和,例如,呼叫DigitSum(1729),則應該返回1+7+2+9,它的和是19 編寫一個
求第n個斐波那契數(不用遞迴的方法,用迴圈)
#define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<stdlib.h> int Fib(int n) { if (n == 1 || n == 2) // |按位或,||邏輯或 { retur
Python 遞迴求第n個斐波那契數
版本2.7 遞迴求第n個斐波那契數,函式要有個出口,目前我理解遞迴的運算都通過最基礎的運算完成。所有經過的運算都要通過出口的基礎值來累加的。 def fib(n): if n==0 or n==1: return n else:
[c語言]用遞迴和非遞迴求第n個斐波那契數
程式碼 //1.1遞迴求第n個斐波那契數 #include<stdio.h> int fib(int n) { if(n<=2) return 1; else return fib(n-1)+fib(n-2); } int main
非遞歸和遞歸分別實現求第n個斐波那契數。
都是 一個 urn nbsp 非遞歸算法 stdio.h include i++ ren 菲波那切數列為:0 1 1 2 3 5 8 13 21 34... 規律:從第三個數字起後面的每一個數字都是前兩個數字的和。 非遞歸算法: 1 #include<stdio.
用遞迴的方法編寫函式求斐波那契級數,觀察遞迴呼叫的過程
#include<iostream> using namespace std; int fbn(int n){ cout<<"呼叫fbn("<<n<<
裴波那契數列的遞迴實現與非遞迴實現
斐波那契數列是數學家列昂納多·斐波那契(Leonardoda Fibonacci[1] )以兔子繁殖為例子而引入,也稱為“兔子數列”。 指的是這樣一個數列:0、1、1、2、3、5、8、13、21、34、…… 在數學上,斐波納契數列以如下被以遞迴的方法定義:F(0)=0,F
斐波那契,非遞迴形式(python)
隨手寫了寫斐波那契函式,貼上上來。 順便膜拜一下python對大數加法的支援。 #Fibonacci, F(0)=0, F(1)=1 def Fib(n): if n == 0:
C語言遞迴與非遞迴實現求第n個斐波那契數
一、非遞迴實現第N個菲波那切數列: 程式如下: #include <stdio.h> int fib(int n) { int a1 = 1; int a2 = 1; int a3
C# 斐波拉契數列求第n個值
斐波拉契數列,求第n個值是多少 有這樣一個數列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,求出第n 位的值 int num1 = 1, num2 = 1, sum = 0; &
