Python例項淺談之四遞迴求斐波那契、階乘、累加和
一、問題
指令碼遞迴求斐波那契、階乘和、累加和函式的執行。先在單執行緒中執行這三個函式,然後在多執行緒中做同樣的事,以說明多執行緒的好處。以及子類化threading執行緒模組的Thread類,靈活地來自定義執行緒物件。
二、解決
1、程式碼
在這個多執行緒程式中,分別在單執行緒和多執行緒環境中,執行三個遞迴函式。在單執行緒中執行只要簡單地逐個呼叫這些函式,在函式結束後,顯示對應的結果;在多執行緒中,不馬上顯示結果,等到要結束時才會呼叫 getResult()函式,並在最後顯示每個函式的結果。Thread的子類更為通用,把子類單獨放在一個模組中。#!/usr/bin/env python import threading from time import time, ctime, sleep class MyThread(threading.Thread): def __init__(self, func, args, name=''): threading.Thread.__init__(self) self.name = name self.func = func self.args = args def getResult(self): return self.res def run(self): print 'starting', self.name, 'at:', ctime() self.res = apply(self.func, self.args) print self.name, 'finished at:', ctime() def fib(x): sleep(0.005) if x < 2: return 1 return (fib(x-2) + fib(x-1)) def fac(x): sleep(0.1) if x < 2: return 1 return (x * fac(x-1)) def sum(x): sleep(0.1) if x < 2: return 1 return (x + sum(x-1)) funcs = (fib, fac, sum) n = 12 def main(): nfuncs = range(len(funcs)) print '*** SINGLE THREAD' for i in nfuncs: print 'starting', funcs[i].__name__, 'at:', ctime() print funcs[i](n) print funcs[i].__name__, 'finished at:', ctime() print '\n*** MULTIPLE THREADS' threads = [] for i in nfuncs: t = MyThread(funcs[i], (n,), funcs[i].__name__) threads.append(t) for i in nfuncs: threads[i].start() for i in nfuncs: threads[i].join() print threads[i].getResult() print '--all DONE at:', ctime() if __name__ == '__main__': main()
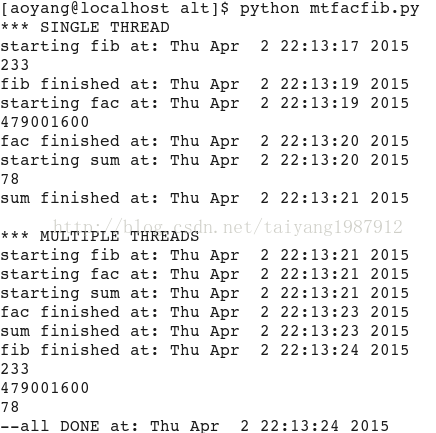
2、執行結果圖
三、總結
(1)在每個函式中加上一個sleep()函式,讓為了讓函式慢下來,以便於能方便地看到多執行緒能在多大程度上加速程式的執行。在實際的開發中應用中可以去掉sleep()函式。(2)執行緒中的臨界資源(臨界區)、鎖機制、條件變數、訊號量、同步佇列等機制在實際開發中還需總結。
(3)若有不足,請留言,在此先感謝!
相關推薦
Python例項淺談之四遞迴求斐波那契、階乘、累加和
一、問題 指令碼遞迴求斐波那契、階乘和、累加和函式的執行。先在單執行緒中執行這三個函式,然後在多執行緒中做同樣的事,以說明多執行緒的好處。以及子類化threading執行緒模組的Thread類,靈活地來自定義執行緒物件。 二、解決 1、程式碼 #!/usr/bin/
Python—用列表和遞迴求斐波那契數列
1.生成前10個斐波那契數(Fibonacci),要求將這些整數存於列表L中,最後打印出這些數[1, 1, 2, 3, 5, 8, 13, 21, 34, 55] (斐波那契數的前兩個是1,1,之後的數是前兩個數的和) 方法1:使用列表 L=[1,1] while len(L)<
用遞迴求斐波那契數
斐波那契數是第一個數和第二個數都為1,從第三個數開始,後面的是是前面相鄰兩個數的和。定義的函式如下所示: int fib(int m) { if (m == 1 || m == 2)
非遞迴求斐波那契數
#define _CRT_SECURE_NO_WARNINGS 1 #include<stdio.h> int fib(int n) { int a = 1; int b = 1; int c = 0; if (n <= 2) re
Java面向物件——用遞迴求斐波那契數列
1.用非遞迴方式求斐波那契數列: package Hello; public class Test { public static void main(String[] args) {
java遞迴求斐波那契數列第n項
public class Fibonacci { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int n = sc.nextInt(); int f
遞迴求斐波那契數列
int f (int n) { if(n==1||n==2) return 1; else return f(n-1)+f(n-2); } #include<stdio.h> int main() {
python 遞迴方法 斐波那契數列—漢諾塔
#普通方法生成 def feibo(n): a,b=0,1 print('0,1',end='') for i in range(n-1): a,b=b,a+b print(',{0}'.format(b),end='') #遞迴方法生成 def
python 迭代法和遞迴 實現斐波那契演算法
題目:古典問題:有一對兔子,從出生後第3個月起每個月都生一對兔子,小兔子長到第三個月後每個月又生一對兔子,假如兔子都不死,問每個月的兔子總數為多少? 1.程式分析: 兔子的規律為數列1,1,2,3,5,8,13,21…. 由規律可知: f(n) = f(n-1)+f(n-2) 符合斐波那契數
Python:遞迴輸出斐波那契數列
今天學習Python的時候做一道練習題,題目是這樣的: 題目 匯入 問題 有一對兔子,從出生後第3個月起每個月都生一對兔子,小兔子長到第三個月後每個月又生一對兔子,假如兔子都不死,問每個月的兔子總對數為多少? 分析 簡單的分析了一下,發現這個問題
如何使用Python的遞迴方法來實現組合數,遞迴實現斐波那契數
組合數公式: C(n,m)=n!/((n-m)!*m!) 傳統演算法 def CombinationNum(n,m): #n>=m n,m都是自然數 #找到一個出口 if m == 0 or n == m: return
C語言經典演算法(八)——遞迴實現斐波那契數列的兩種方法
後繼續整理演算法並寫出自己的理解和備註。 C++實現的:遞迴實現斐波那契數列 1、 遞迴實現斐波那契數列Fib(n) <1> 題目描述:輸入n值,求解第n項的斐波那契數列值 <2> 方法一:概念法 <3> 方法二:遞迴法 斐波那契數列值是值1
用遞迴和非遞迴實現斐波那契數列
斐波那契數列(Fibonacci sequence),又稱黃金分割數列、因數學家列昂納多·斐波那契(Leonardoda Fibonacci)以兔子繁殖為例子而引入,故又稱為“兔子數列”,指的是這樣一個數列:1、1、2、3、5、8、13、21、34、……在數學上,斐波納契數列
用for迴圈\遞迴寫斐波那契數列
for迴圈 public class Test{ public static int fib(int n){ if(n == 1 || n == 2){ return 1; }else{ int a = 1; int b = 1; int s = 0; for
使用遞迴實現斐波那契列數中的20個月有多少隻兔子
package it.casts.homework; //5.使用遞迴實現斐波那契列數中的20個月有多少隻兔子; public class Test05 { public static void main(String[] args) { int method = method(20);
遞迴:斐波那契數列(兔子總數)。
反覆學習反覆學習。 因為自己對遞迴還是不太熟練,於是做POJ1753的時候就很吃力,就是翻棋子直到棋盤上所有棋子的顏色一樣為止,求最少翻多少次,方法是列舉遞迴。然後就打算先做另一道遞迴的題(從陣列中取
java遞迴實現斐波那契數列
/** *create Date:2016-12-23 *modified Date:2016-12-23 *modified by:shark *Description:斐波那契數列 **/ public class Shulie{public static long d
使用JavaScript實現遞迴解決斐波那契數列及優化
遞迴的概念:若一個演算法直接地或間接地呼叫自己本身,則稱這個演算法是遞迴演算法(《資料結構—使用C語言實現;朱戰立;西安交大出版社》); 遞迴的兩個條件:自己呼叫自己和有結束條件(否則是死遞迴) 斐波那契數列 1, 1, 2,3,5,8,13,21….. 使
遞迴算斐波那契數列
#include<stdio.h> long Fib(int n); int count;//計算函式被呼叫的次數 int main() { int n,i,x; printf("Input n:"); scanf("%d",&n); for(i=1;i<=
演算法 遞迴與斐波那契
1 遞迴 把遞迴想成方法棧,後進先出。遞:一層一層深入(依次執行前置程式碼),直到到達遞迴終止條件(一定要有終止條件,不再執行自己),歸:再從底層一層一層返回(依次執行後置程式碼)。 快速排序:典型的遞迴前置思想,先執行取中分邊,再左右向下遞迴 歸併排序:典型的遞迴後置思想