1. 前言

前面九講對神經網路的結構，元件，訓練方法，原理等做了介紹。現在我們回到本系列的核心：計算機視覺，神經網路中的一種特殊版本在計算機視覺中使用最為廣泛，這就是大家都知道的卷積神經網路。卷積神經網路和普通的神經網路一樣，由『神經元』按層級結構組成，其間的權重和偏移量都是可訓練得到的。同樣是輸入的資料和權重做運算，輸出結果輸入激勵神經元，輸出結果。從整體上看來，整個神經網路做的事情，依舊是對於畫素級別輸入的影象資料，用得分函式計算最後各個類別的得分，然後我們通過最小化損失函式來得到最優的權重。之前的博文中介紹的各種技巧和訓練方法，以及注意事項，在這個特殊版本的神經網路上依舊好使。

既然提到卷積神經網路了，我們就來說說它的特殊之處，首先這裡的卷積神經網路一般假定輸入就是圖片資料，也正是因為輸入是圖片資料，我們可以利用它的畫素結構特性，去做一些假設來簡化神經網路的訓練複雜度(減少訓練引數個數)。

2.卷積神經網總體結構一覽

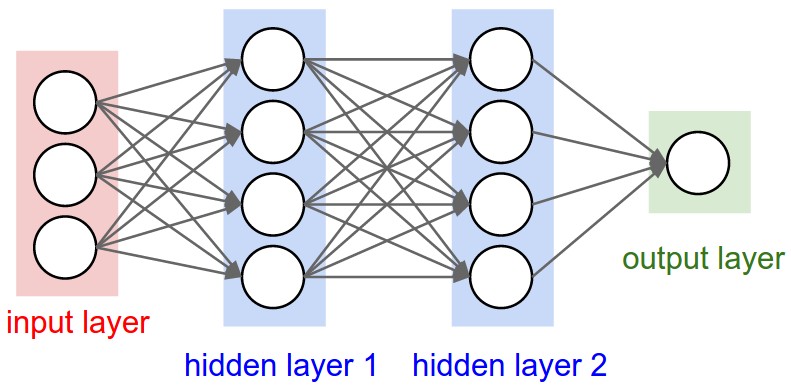
我們前面講過的神經網路結構都比較一致，輸入層和輸出層中間夾著數層隱藏層，每一層都由多個神經元組成，層和層之間是全連線的結構，同一層的神經元之間沒有連線。

卷積神經網路是上述結構的一種特殊化處理，因為對於影象這種資料而言，上面這種結構實際應用起來有較大的困難：就拿CIFAR-10舉例吧，圖片已經很小了，是32*32*3(長寬各32畫素，3個顏色通道)的，那麼在神經網路當中，我們只看隱藏層中的一個神經元，就應該有32*32*3=3072個權重，如果大家覺得這個權重個數的量還行的話，再設想一下，當這是一個包含多個神經元的多層神經網(假設n個)，再比如影象的質量好一點(比如是200*200*3的)，那將有200*200*3*n= 120000n個權重需要訓練，結果是拉著這麼多引數訓練，基本跑不動，跑得起來也是『氣喘吁吁』，當然，最關鍵的是這麼多引數的情況下，分分鐘模型就過擬合了。別急，別急，一會兒我們會提到卷積神經網路的想法和簡化之處。

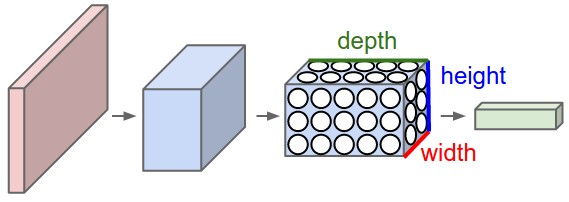
卷積神經網路結構比較固定的原因之一，是圖片資料本身的合理結構，類影象結構(200*200*3)，我們也把卷積神經網路的神經元排布成 width*height*depth的結構，也就是說這一層總共有width*height*depth個神經元，如下圖所示。舉個例子說，CIFAR-10的輸出層就是1*1*10維的。另外我們後面會說到，每一層的神經元，其實只和上一層裡某些小區域進行連線，而不是和上一層每個神經元全連線。

3.卷積神經網路的組成層

在卷積神經網路中，有3種最主要的層：

• 卷積運算層
• pooling層
• 全連線層

一個完整的神經網路就是由這三種層疊加組成的。

結構示例

我們繼續拿CIFAR-10資料集舉例，一個典型的該資料集上的卷積神經網路分類器應該有[INPUT - CONV - RELU - POOL - FC]的結構，具體說來是這樣的：

• INPUT[32*32*3]包含原始圖片資料中的全部畫素，長寬都是32，有RGB 3個顏色通道。
• CONV卷積層中，沒個神經元會和上一層的若干小區域連線，計算權重和小區域畫素的內積，舉個例子可能產出的結果資料是[32*32*12]的。
• RELU層，就是神經元激勵層，主要的計算就是max(0,x)，結果資料依舊是[32*32*12]。
• POOLing層做的事情，可以理解成一個下采樣，可能得到的結果維度就變為[16*16*12]了。
• 全連線層一般用於最後計算類別得分，得到的結果為[1*1*10]的，其中的10對應10個不同的類別。和名字一樣，這一層的所有神經元會和上一層的所有神經元有連線。

這樣，卷積神經網路作為一箇中間的通道，就一步步把原始的影象資料轉成最後的類別得分了。有一個點我們要提一下，剛才說到了有幾種不同的神經網路層，其中有一些層是有待訓練引數的，另外一些沒有。詳細一點說，卷積層和全連線層包含權重和偏移的；而RELU和POOLing層只是一個固定的函式運算，是不包含權重和偏移引數的。不過POOLing層包含了我們手動指定的超引數，這個我們之後會提到。

總結一下：

• 一個卷積神經網路由多種不同型別的層(卷幾層/全連線層/RELU層/POOLing層等)疊加而成。
• 每一層的輸入結構是3維的資料，計算完輸出依舊是3維的資料。
• 卷積層和全連線層包含訓練引數，RELU和POOLing層不包含。
• 卷積層，全連線層和POOLing層包含超引數，RELU層沒有。

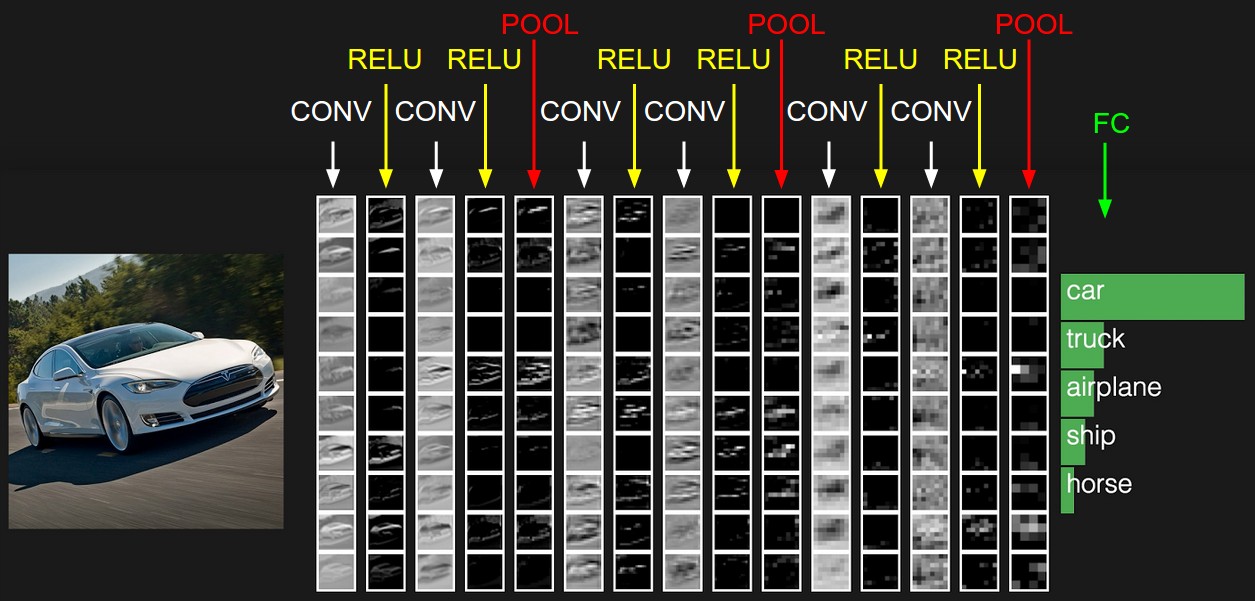
下圖為CIFAR-10資料集構建的一個卷積神經網路結構示意圖：

既然有這麼多不同的層級結構，那我們就展開來講講：

3.1 卷積層

說起來，這是卷積神經網路的核心層(從名字就可以看出來對吧-_-||)。

3.1.1 卷積層綜述

直觀看來，卷積層的引數其實可以看做，一系列的可訓練/學習的過濾器。在前向計算過程中，我們輸入一定區域大小(width*height)的資料，和過濾器點乘後等到新的二維資料，然後滑過一個個濾波器，組成新的3維輸出資料。而我們可以理解成每個過濾器都只關心過濾資料小平面內的部分特徵，當出現它學習到的特徵的時候，就會呈現啟用/activate態。

區域性關聯度。這是卷積神經網路的獨特之處其中之一，我們知道在高維資料(比如圖片)中，用全連線的神經網路，實際工程中基本是不可行的。卷積神經網路中每一層的神經元只會和上一層的一些區域性區域相連，這就是所謂的區域性連線性。你可以想象成，上一層的資料區，有一個滑動的視窗，只有這個視窗內的資料會和下一層神經元有關聯，當然，這個做法就要求我們手動敲定一個超引數:視窗大小。通常情況下，這個視窗的長和寬是相等的，我們把長x寬叫做receptive field。實際的計算中，這個視窗是會『滑動』的，會近似覆蓋圖片的所有小區域。

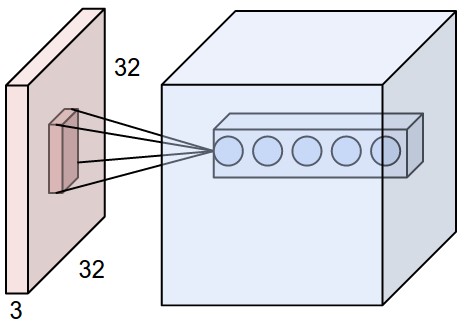
舉個例項，CIFAR-10中的圖片輸入資料為[32*32*3]的，如果我們把receptive field設為5*5，那receptive field的data都會和下一層的神經元關聯，所以共有5*5*3=75個權重，注意到最後的3依舊代表著RGB 3個顏色通道。

如果不是輸入資料層，中間層的data格式可能是[16*16*20]的，假如我們取3*3的receptive field，那單個神經元的權重為3*3*20=180。

區域性關聯細節。我們剛才說到卷積層的區域性關聯問題，這個地方有一個receptive field，也就是我們直觀理解上的『滑動資料視窗』。從輸入的資料到輸出資料，有三個超引數會決定輸出資料的維度，分別是深度/depth，步長/stride 和 填充值/zero-padding：

1. 所謂深度/depth，簡單說來指的就是卷積層中和上一層同一個輸入區域連線的神經元個數。這部分神經元會在遇到輸入中的不同feature時呈現activate狀態，舉個例子，如果這是第一個卷積層，那輸入到它的資料實際上是畫素值，不同的神經元可能對影象的邊緣。輪廓或者顏色會敏感。
2. 所謂步長/stride，是指的視窗從當前位置到下一個位置，『跳過』的中間資料個數。比如從影象資料層輸入到卷積層的情況下，也許視窗初始位置在第1個畫素，第二個位置在第5個畫素，那麼stride=5-1=4.
3. 所謂zero-padding是在原始資料的周邊補上0值的圈數。(下面第2張圖中的樣子)

這麼解釋可能理解起來還是會有困難，我們找兩張圖來對應一下這三個量：

這是解決ImageNet分類問題用到的卷積神經網路的一部分，我們看到卷積層直接和最前面的影象層連線。影象層的維度為[227*227*3]，而receptive field設為11*11，圖上未標明，但是滑動視窗的步長stride設為4，深度depth為48+48=96(這是雙GPU並行設定)，邊緣沒有補0，因此zero-padding為0，因此視窗滑完一行，總共停留次數為(data_len-receptive_field_len+2*zero-padding)/stride+1=(227-11+2*0)/4+1=55，因為影象的長寬相等，因此縱向視窗數也是55，最後得到的輸出資料維度為55*55*96維。

這是一張動態的卷積層計算圖，圖上的zero-padding為1，所以大家可以看到資料左右各補了一行0，視窗的長寬為3，滑動步長stride為2。

關於zero-padding，補0這個操作產生的根本原因是，為了保證視窗的滑動能從頭剛好到尾。舉個例子說，上2圖中的上面一幅圖，因為(data_len-receptive_field_len+2*zero-padding)/stride剛好能夠整除，所以視窗左側貼著資料開始位置，滑到尾部剛好視窗右側能夠貼著資料尾部位置，因此是不需要補0的。而在下面那幅圖中，如果滑動步長設為4，你會發現第一次計算之後，視窗就無法『滑動』了，而尾部的資料，是沒有被視窗『看到過』的，因此補0能夠解決這個問題。

關於視窗滑動步長。大家可以發現一點，視窗滑動步長設定越小，兩次滑動取得的資料，重疊部分越多，但是視窗停留的次數也會越多，運算律大一些；視窗滑動步長設定越長，兩次滑動取得的資料，重疊部分越少，視窗停留次數也越少，運算量小，但是從一定程度上說資料資訊不如上面豐富了。

3.1.2 卷積層的引數共享

首先得說卷積層的引數共享是一個非常讚的處理方式，它使得卷積神經網路的訓練計算複雜度和引數個數降低非常非常多。就拿實際解決ImageNet分類問題的卷積神經網路結構來說，我們知道輸出結果有55*55*96=290400個神經元，而每個神經元因為和視窗內資料的連線，有11*11*3=363個權重和1個偏移量。所以總共有290400*364=105705600個權重。。。然後。。。恩，訓練要累掛了。。。

因此我們做了一個大膽的假設，我們剛才提到了，每一個神經元可以看做一個filter，對圖片中的資料窗區域做『過濾』。那既然是filter，我們乾脆就假設這個神經元用於連線資料窗的權重是固定的，這意味著，對同一個神經元而言，不論上一層資料視窗停留在哪個位置，連線兩者之間的權重都是同一組數。那代表著，上面的例子中的卷積層，我們只需要 神經元個數*資料視窗維度=96*11*11*3=34848個權重。

如果對應每個神經元的權重是固定的，那麼整個計算的過程就可以看做，一組固定的權重和不同的資料視窗資料做內積的過程，這在數學上剛好對應『卷積』操作，這也就是卷積神經網的名字來源。另外，因為每個神經元的權重固定，它可以看做一個恆定的filter，比如上面96個神經元作為filter視覺化之後是如下的樣子：

需要說明的一點是，引數共享這個策略並不是每個場景下都合適的。有一些特定的場合，我們不能把圖片上的這些視窗資料都視作作用等同的。一個很典型的例子就是人臉識別，一般人的面部都集中在影象的中央，因此我們希望，資料視窗滑過這塊區域的時候，權重和其他邊緣區域是不同的。我們有一種特殊的層對應這種功能，叫做區域性連線層/Locally-Connected Layer

3.1.3 卷積層的簡單numpy實現

我們假定輸入到卷積層的資料為X，加入X的維度為X.shape: (11,11,4)。假定我們的zero-padding為0，也就是左右上下不補充0資料，資料視窗大小為5，視窗滑動步長為2。那輸出資料的長寬應該為(11-5)/2+1=4。假定第一個神經元對應的權重和偏移量分別為W0和b0，那我們就能算得，在第一行資料視窗停留的4個位置，得到的結果值分別為：

• V[0,0,0] = np.sum(X[:5,:5,:] * W0) + b0
• V[1,0,0] = np.sum(X[2:7,:5,:] * W0) + b0
• V[2,0,0] = np.sum(X[4:9,:5,:] * W0) + b0
• V[3,0,0] = np.sum(X[6:11,:5,:] * W0) + b0

注意上述計算過程中，*運算子是對兩個向量進行點乘的，因此W0應該維度為(5,5,4)，同樣你可以計算其他位置的計算輸出值：

• V[0,0,1] = np.sum(X[:5,:5,:] * W1) + b1
• V[1,0,1] = np.sum(X[2:7,:5,:] * W1) + b1
• V[2,0,1] = np.sum(X[4:9,:5,:] * W1) + b1
• V[3,0,1] = np.sum(X[6:11,:5,:] * W1) + b1
• …

每一個神經元對應不同的一組W和b，在每個資料視窗停留的位置，得到一個輸出值。

我們之前提到了卷積層在做的事情，是不斷做權重和視窗資料的點乘和求和。因此我們也可以把這個過程整理成一個大的矩陣乘法。

1. 看看資料端，我們可以做一個操作im2col將資料轉成一個可直接供神經元filter計算的大矩陣。舉個例子說，輸入是[227*227*3]的圖片，而神經元權重為[11*11*3]，同時視窗移動步長為4，那我們知道資料視窗滑動過程中總共產生[(227-11)/4+1]*[(227-11)/4+1]=55*55=3025個區域性資料區域，又每個區域包含11*11*3=363個數據值，因此我們想辦法把原始資料重複和擴充成一個[363*3025]的資料矩陣X_col，就可以直接和filter進行運算了。
2. 對於filter端(卷積層)，假如厚度為96(有96個不同權重組的filter)，每個filter的權重為[11*11*3]，因此filter矩陣W_row維度為[96*363]
3. 在得到上述兩個矩陣後，我們的輸出結果即可以通過np.dot(W_row, X_col)計算得到，結果資料為[96*3025]維的。

這個實現的弊端是，因為資料視窗的滑動過程中有重疊，因此我們出現了很多重複資料，佔用記憶體較大。好處是，實際計算過程非常簡單，如果我們用類似BLAS這樣的庫，計算將非常迅速。

另外，在反向傳播過程中，其實卷積對應的操作還是卷積，因此實現起來也很方便。

3.2 Pooling層

簡單說來，在卷積神經網路中，Pooling層是夾在連續的卷積層中間的層。它的作用也非常簡單，就是**逐步地壓縮/減少資料和引數的量，也在一定程度上減小過擬合的現象。**Pooling層做的操作也非常簡單，就是將原資料上的區域壓縮成一個值(區域最大值/MAX或者平均值/AVERAGE)，最常見的Pooling設定是，將原資料切成2*2的小塊，每塊裡面取最大值作為輸出，這樣我們就自然而然減少了75%的資料量。需要提到的是，除掉MAX和AVERAGE的Pooling方式，其實我們也可以設定別的pooling方式，比如L2範數pooling。說起來，歷史上average pooling用的非常多，但是近些年熱度降了不少，工程師們在實踐中發現max pooling的效果相對好一些。

一個對Pooling層和它的操作直觀理解的示意圖為：

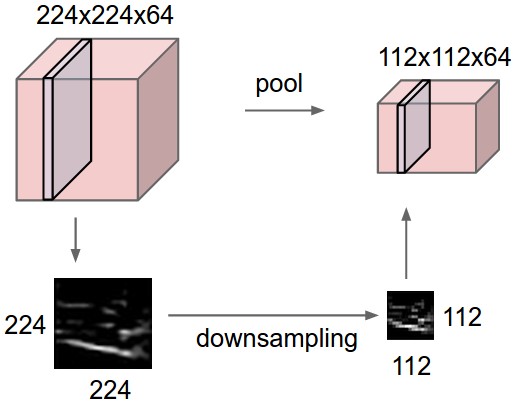
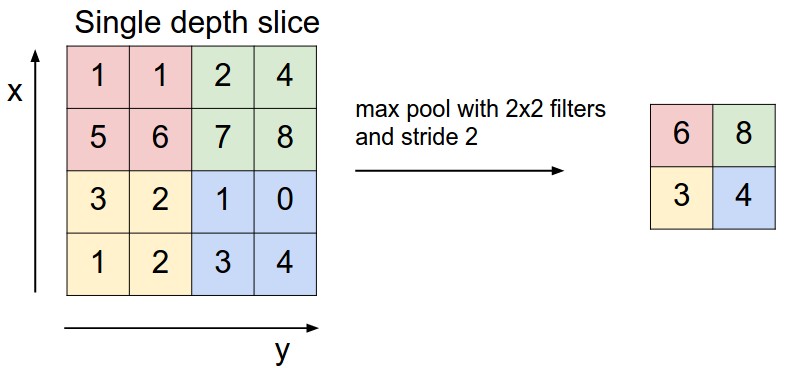
上圖為Pooling層的一個直觀示例，相當於對厚度為64的data，每一個切片做了一個下采樣。下圖為Pooling操作的實際max操作。

Pooling層(假定是MAX-Pooling)在反向傳播中的計算也是很簡單的，大家都知道如何去求max(x,y)函式的偏導（也是分段的）。

3.3 歸一化層(Normalization Layer)

卷積神經網路裡面有時候會用到各種各樣的歸一化層，尤其是早期的研究，經常能見到它們的身影，不過近些年來的研究表明，似乎這個層級對最後結果的幫助非常小，所以後來大多數時候就乾脆拿掉了。

3.4 全連線層

這是我們在介紹神經網路的時候，最標準的形式，任何神經元和上一層的任何神經元之間都有關聯，然後矩陣運算也非常簡單和直接。現在的很多卷積神經網路結構，末層會採用全連線去學習更多的資訊。

4. 搭建卷積神經網結構

從上面的內容我們知道，卷積神經網路一般由3種層搭建而成：卷積層，POOLing層(我們直接指定用MAX-Pooling)和全連線層。然後我們一般選用最常見的神經元ReLU，我們來看看有這些『元件』之後，怎麼『拼』出一個合理的卷積神經網。

4.1 層和層怎麼排

最常見的組合方式是，用ReLU神經元的卷積層組一個神經網路，同時在卷積層和卷積層之間插入Pooling層，經過多次的[卷積層]=>[Pooling層]疊加之後，資料的總體量級就不大了，這個時候我們可以放一層全連線層，然後最後一層和output層之間是一個全連線層。所以總結一下，最常見的卷積神經網結構為：

[輸入層] => [[ReLU卷積層]*N => [Pooling層]?]*M => [ReLU全連線層]*K => [全連線層]

解釋一下，其中\*操作代表可以疊加很多層，而[Pooling層]?表示Pooling層其實是可選的，可有可無。N和M是具體層數。比如說[輸入層] -> [[ReLU卷積層]=>[ReLU卷積層]=>[Pooling層]]*3 -> [ReLU全連線層]*2 -> [全連線層]就是一個合理的深層的卷積神經網。

『在同樣的視野範圍內，選擇多層疊加的卷積層，而不是一個大的卷積層』

這句話非常拗口，但這是實際設計卷積神經網路時候的經驗，我們找個例子來解釋一下這句話：如果你設計的卷積神經網在資料層有3層連續的卷積層，同時每一層滑動資料視窗為3*3，第一層每個神經元可以同時『看到』3*3的原始資料層，那第二層每個神經元可以『間接看到』(1+3+1)*(1+3+1)=5*5的資料層內容，第三層每個神經元可以『間接看到』(1+5+1)*(1+5+1)=7*7的資料層內容。那從最表層看，還不如直接設定滑動資料視窗為7*7的，為啥要這麼設計呢，我們來分析一下優劣：

• 雖然第三層對資料層的『視野』範圍是一致的。但是單層卷積層加7*7的上層滑動資料視窗，結果是這7個位置的資料，都是線性組合後得到最後結果的；而3層卷積層加3*3的滑動資料視窗，得到的結果是原資料上7*7的『視野』內資料多層非線性組合，因此這樣的特徵也會具備更高的表達能力。
• 如果我們假設所有層的『厚度』/channel數是一致的，為C，那7*7的卷積層，會得到C×(7×7×C)=49C2個引數，而3層疊加的3*3卷積層只有3×(C×(3×3×C))=27C2個引數。在計算量上後者顯然是有優勢的。
• 同上一點，我們知道為了反向傳播方便，實際計算過程中，我們會在前向計算時保留很多中間梯度，3層疊加的3*3卷積層需要保持的中間梯度要小於前一種情況，這在工程實現上是很有好處的。

4.2 層大小的設定

話說層級結構確定了，也得知道每一層大概什麼規模啊。現在我們就來聊聊這個。說起來，每一層的大小(神經元個數和排布)並沒有嚴格的數字規則，但是我們有一些通用的工程實踐經驗和係數：

• 對於輸入層(影象層)，我們一般把資料歸一化成2的次方的長寬畫素值。比如CIFAR-10是32*32*3，STL-10資料集是64*64*3，而ImageNet是224*224*3或者512*512*3。
• 卷積層通常會把每個[濾子/filter/神經元]對應的上層滑動資料視窗設為3*3或者5*5，滑動步長stride設為1(工程實踐結果表明stride設為1雖然比較密集，但是效果比較好，步長拉太大容易損失太多資訊)，zero-padding就不用了。
• Pooling層一般採用max-pooling，同時設定取樣視窗為2*2。偶爾會見到設定更大的取樣視窗，但是那意味著損失掉比較多的資訊了。
• 比較重要的是，我們得預估一下記憶體，然後根據記憶體的情況去設定合理的值。我們舉個例子，在ImageNet分類問題中，圖片是224*224*3的，我們跟在資料層後面3個3*3『視野窗』的卷積層，每一層64個filter/神經元,把padding設為1，那麼最後每個卷積層的output都是[224*224*64]，大概需要1000萬次對output的激勵計算(非線性activation)，大概花費72MB記憶體。而工程實踐裡，一般訓練都在GPU上進行，GPU的記憶體比CPU要吃緊的多，所以也許我們要稍微調動一下引數。比如AlexNet用的是11*11的的視野窗，滑動步長為4。

4.3 典型的工業界在用卷積神經網路

幾個有名的卷積神經網路如下：

• LeNet，這是最早用起來的卷積神經網路，Yann LeCun在論文LeNet提到。
• AlexNet，2012 ILSVRC比賽遠超第2名的卷積神經網路，和LeNet的結構比較像，只是更深，同時用多層小卷積層疊加提到大卷積層。
• ZF Net，2013 ILSVRC比賽冠軍，可以參考論文ZF Net
• GoogLeNet，2014 ILSVRC比賽冠軍，Google發表的論文Going Deeper with Convolutions有具體介紹。
• VGGNet，也是2014 ILSVRC比賽中的模型，有意思的是，即使這個模型當時在分類問題上的效果，略差於google的GoogLeNet，但是在很多影象轉化學習問題(比如object detection)上效果奇好，它也證明卷積神經網的『深度』對於最後的效果有至關重要的作用。預訓練好的模型在pretrained model site可以下載。

具體一點說來，VGGNet的層級結構和花費的記憶體如下：

INPUT: [224x224x3]        memory:  224*224*3=150K   weights: 0
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*3)*64 = 1,728
CONV3-64: [224x224x64]  memory:  224*224*64=3.2M   weights: (3*3*64)*64 = 36,864
POOL2: [112x112x64]  memory:  112*112*64=800K   weights: 0
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*64)*128 = 73,728
CONV3-128: [112x112x128]  memory:  112*112*128=1.6M   weights: (3*3*128)*128 = 147,456
POOL2: [56x56x128]  memory:  56*56*128=400K   weights: 0
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*128)*256 = 294,912
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
CONV3-256: [56x56x256]  memory:  56*56*256=800K   weights: (3*3*256)*256 = 589,824
POOL2: [28x28x256]  memory:  28*28*256=200K   weights: 0
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*256)*512 = 1,179,648
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [28x28x512]  memory:  28*28*512=400K   weights: (3*3*512)*512 = 2,359,296
POOL2: [14x14x512]  memory:  14*14*512=100K   weights: 0
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
CONV3-512: [14x14x512]  memory:  14*14*512=100K   weights: (3*3*512)*512 = 2,359,296
POOL2: [7x7x512]  memory:  7*7*512=25K  weights: 0
FC: [1x1x4096]  memory:  4096  weights: 7*7*512*4096 = 102,760,448
FC: [1x1x4096]  memory:  4096  weights: 4096*4096 = 16,777,216
FC: [1x1x1000]  memory:  1000 weights: 4096*1000 = 4,096,000

TOTAL memory: 24M * 4 bytes ~= 93MB / image (only forward! ~*2 for bwd)
TOTAL params: 138M parameters

有意思的是，大家會注意到，在VGGNet這樣一個神經網路裡，大多數的記憶體消耗在前面的卷積層，而大多數需要訓練的引數卻集中在最後的全連線層，比如上上面的例子裡，全連線層有1億權重引數，總共神經網裡也就1.4億權重引數。

4.4 考慮點

組一個實際可用的卷積神經網路最大的瓶頸是GPU的記憶體。畢竟現在很多GPU只有3/4/6GB的記憶體，最大的GPU也就12G記憶體，所以我們應該在設計卷積神經網的時候多加考慮：

• 很大的一部分記憶體開銷來源於卷積層的激勵函式個數和儲存的梯度數量。
• 儲存的權重引數也是記憶體的主要消耗處，包括反向傳播要用到的梯度，以及你用momentum, Adagrad, or RMSProp這些演算法時候的中間儲存值。
• 資料batch以及其他的類似版本資訊或者來源資訊等也會消耗一部分記憶體。

5. 更多的卷積神經網路參考資料

參考資料與原文