利用二叉樹的非遞迴後序遍歷求解最近公共祖先問題
通過上一篇的部落格我們知道,可以利用棧來實現二叉樹的後序遍歷。其實這裡有一個性質,就是當使用非遞迴後序遍歷時,棧中的元素就是當前節點到根節點的路徑。利用這個規律,我們就可以求解最近公共最先問題了。
演算法
- 找出兩個節點各自到根節點的路徑。這裡利用非遞迴後序遍歷二叉樹,既可以找到兩個節點到根節點的路徑。
- 根據路徑找出最近的公共祖先。首先根節點肯定是他們的祖先,可以從跟節點開始查詢,直到最後一個相同的樹節點,就是他們的公共祖先了。
實現
///求兩個節點的最大公共祖先
void BiTree::ancestor(char A,char B){
vector<BiNode *> 測試
#include <iostream>
#include "BiTree.h"
using namespace std;
int main()
{
BiTree a;
string s;
s="ABD##E#F##C##";
a.createBiTree(s);
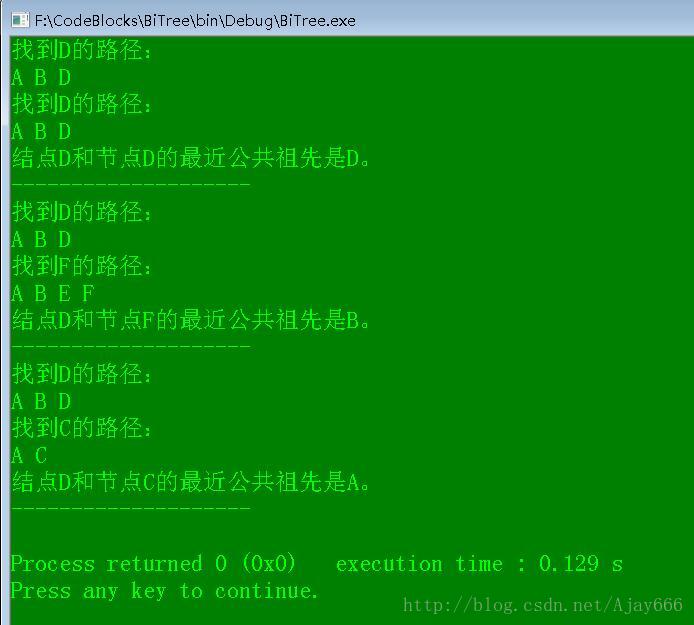
a.ancestor('D','D');
cout<<"--------------------"<<endl;
a.ancestor('D','F');
cout<<"--------------------"<<endl;
a.ancestor('D','C');
cout<<"--------------------"<<endl;
return 0;
}
相關推薦
利用二叉樹的非遞迴後序遍歷求解最近公共祖先問題
通過上一篇的部落格我們知道,可以利用棧來實現二叉樹的後序遍歷。其實這裡有一個性質,就是當使用非遞迴後序遍歷時,棧中的元素就是當前節點到根節點的路徑。利用這個規律,我們就可以求解最近公共最先問題了。 演算法 找出兩個節點各自到根節點的路徑。這裡利
【LeetCode-面試演算法經典-Java實現】【145-Binary Tree Postorder Traversal(二叉樹非遞迴後序遍歷)】
原題 Given a binary tree, return the postorder traversal of its nodes’ values. For exampl
二叉樹非遞迴後序遍歷演算法
與正常的非遞迴中序遍歷演算法不同於兩點: 一 比正常的中序遍歷演算法多了對資料元素的標記。 在壓資料元素入棧(標記記為0,用來表示訪問了其左子樹)時標記, 還有訪問完左子樹利用gettop()獲取雙親通過p=p->rchild進一步訪問右子
【leetcode】145Binary Tree Postorder Traversal(二叉樹非遞迴後序遍歷)
二叉樹後序遍歷非遞迴方法很多書和部落格已經講的很清楚啦,這裡就是記錄一下方便自己日後看 基本思路是: 利用棧來實現 先找到最左節點,過程中的節點都入棧 如果該節點沒有右孩子或前一步訪問了右孩子(根據後序遍歷二叉樹的特點可以知道,如果當前節點有右孩子,則訪問當前節點前一定是
棧實現二叉樹非遞迴先序遍歷
#include "stdio.h" #include "stdlib.h" typedef struct TreeNode *Tree; typedef char ElementType; typedef struct stack *Stack; typedef Tree
java二叉樹非遞迴之中序遍歷
思路:使用輔助棧改寫遞迴程式,中序遍歷沒有前序遍歷好寫,其中之一就在於入棧出棧的順序和限制規則。我們採用「左根右」的訪問順序可知主要由如下四步構成。 步驟: 1.首先需要一直對左子樹迭代並將非空節點入棧 2.節點指標為
二叉樹的前中後序遍歷(遞迴和非遞迴版本)
各位讀者週末愉快呀,今天我想來說說一道很常見的面試題目 —— 關於二叉樹前中後序遍歷的實現。本文將以遞迴和非遞迴方式實現這 3 種遍歷方式,程式碼都比較短,可以放心食用。 先簡單說明一下這 3 種遍歷方式有什麼不同 —— 對於每種遍歷,樹中每個結點都需要經過 3 次(對於葉結點,其左右子樹視為空子樹),但前
每日一題之 非遞迴後序遍歷列印二叉樹所有路徑
描述 給一個二叉樹,列印其所有路徑 思路: 利用後序非遞迴遍歷,因為後序非遞迴遍歷的特性,對於每次訪問的節點,棧裡面存的元素都是當前節點的祖先,所以只要判斷當前節點是不是葉子節點,如果是葉子節點,那麼將棧中元素取出,和當前葉子節點組成一條路徑。 #include <
二叉樹的前中後序遍歷(遞迴+非遞迴)
/** * 二叉樹節點類 * @author wj * */ class TreeNode{ int value; TreeNode left_Node; TreeNode right_Node; public TreeNode(int value) { this.value
二叉樹的前中後序遍歷(遞迴&非遞迴)
中序遞迴: class Solution { public: vector<int> res; vector<int> inorderTraversal(Tre
二叉樹非遞迴前序建立與後序遍歷
建立過程:通過棧來模擬遞迴建立。先將根壓入棧中,然後不斷的加左子樹,遇到空則加右子樹;在開始不斷的加左子樹...一直 重複下去直到讀取到回車。(建立時
二叉樹的前中後序遍歷(遞迴&非遞迴)
中序遞迴: class Solution { public: vector<int> res; vector<int> inorderTraversal(TreeNode * root) { inorder(root);
二叉樹非遞迴前序、中序、後序遍歷
import java.util.Stack; class Solution { private static void doPre(ListNode root) { &n
c語言實現二叉樹(二叉連結串列)非遞迴後序遍歷
演算法思想 因為後序遍歷是先訪問左子樹,再訪問右子樹,最後訪問根節點。當用棧實現遍歷時,必須分清返回根節點時,是從左子樹返回的還是從右子樹返回的。所以使用輔助指標r指向最近已訪問的結點。當然也可以在節點中增加一個標誌域,記錄是否已被訪問。 #include<iost
二叉樹模板 先中後序遍歷,非遞迴演算法,層次遍歷,葉子結點數,深度
#include <iostream> #include<stdio.h> #include<malloc.h> #include<queue> #define MAX 50 using namespace std; type
資料結構--二叉樹的遍歷--求二叉樹的深度(後序遍歷)
二叉樹為空:深度為0; 二叉樹為0:深度為1; 一般的二叉樹:深度=max{左子樹的深度,右子樹的深度} + 1。 int Depth (BiTree T) { if (!T)//如果二叉樹根節點為空,則深度為0 depthval=0; else {
二叉樹的前中後序遍歷
本文介紹二叉樹的前序,中序和後序遍歷,採用遞迴和非遞迴兩種方式實現。除此之外,還介紹了對二叉樹按層遍歷的方法。對樹的前中後序遍歷是深度優先搜尋的策略,因此用棧實現。對樹的按層遍歷是廣度優先搜尋,因此採用佇列實現。 樹的前序,中序和後序遍歷,都是針對父節點而言的。 二叉樹的定
二叉連結串列建立一棵二叉樹並進行前中後序遍歷
原始碼:#include<iostream>using namespace std;typedef char Datatype;struct TNode{ Datatype data; TNode* rchild; TNode* lchild;}
資料結構-----後序遍歷二叉樹非遞迴演算法(利用堆疊實現)
一、非遞迴後序遍歷演算法思想 後序遍歷的非遞迴演算法中節點的進棧次數是兩個,即每個節點都要進棧兩次,第二次退棧的時候才訪問節點。 第一次進棧時,在遍歷左子樹的過程中將"根"節點進棧,待左子樹訪問完後,回溯的節點退棧,即退出這個"根"節點,但不能立即訪問,只能藉助於這個"根"
二叉樹非遞迴版的後序遍歷演算法
你會學到什麼? 樹的遞迴遍歷演算法很容易理解,程式碼也很精簡,但是如果想要從本質上理解二叉樹常用的三種遍歷方法,還得要思考樹的非遞迴遍歷演算法。 讀完後的收穫: 將學到二叉樹的後序遍歷的非遞迴版本 明白棧這種資料結構該怎麼使用 討論的問題是什麼?