1 Dijkstra演算法

問題描述：在一個圖中，給定指定頂點，求該頂點到其它頂點的最短距離。

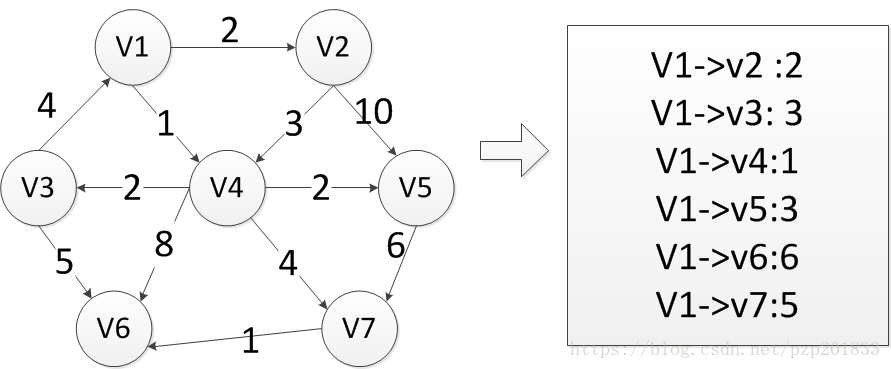
如圖所示：這是一個有向圖，現在要求解從頂點V1到其它頂點的最短距離。以上圖為例，利用Dijkstra演算法求解最短距離。

步驟：

（1）將所有頂點分為兩組，一組是未知的即為S,一組是已知的記為W。開始時，S={V1,V2,V3,V4,V5,V6,V7},W={};

(2)首先選擇頂點V1到其它頂點中距離最短的頂點為已知頂點。顯然V1->v1=0為最小值。這時S={V2,V3,V4,V5,V6,V7},W={V1};

更新距離表格：

（3）接著在已知的距離中，v1->v4的距離最短，將頂點4放入已知的序列中。這時S={V2,V3,V5,V6,V7},W={V1，V4},更新距離表格。

（4） 重複上述過程，在未知頂點中，選擇距離最小的作為已知的，V1->V2=2是最小的，選擇V2作為已知的。此時，S={V3,V5,V6,V7},W={V1，V4，V2},更新距離。

（5）重複上述過程，分別是V5和V3被選為已知的，此時，S={V6,V7},W={V1，V4，V2,V5，V3}。更新距離表格後得到：

（6）比較可知，選擇V7作為已知的，此時，S={V6},W={V1，V4，V2,V5，V3，V7}。更新距離表格後得到：

（7）最後選擇V6,更新距離，演算法結束。最終結果如下圖所示：

具體程式碼如下：

void Dijkstra(const vector<vector<int>>& path, vector<bool>& flag,vector<int>& res,int v)
{
    const int n=flag.size();
    for(int i=0;i<n;++i)
    {
        res[i]=path[v][i];
    }
    flag[v]=true;
    for(int i=0;i<n;++i)
    {
        int tmp=maxint;// const int maxint=INT_MAX
        int u=v;
        for(int j=0;j<n;++j)
        {
            if(!flag[j]&&res[j]<tmp)
            {
               u=j;
               tmp=res[j];
            }
        }
        flag[u]=true;
        for(int j=0;j<n;++j)
        {
            if(!flag[j]&&path[u][j]<maxint)
            {
                res[j]=min(res[j],res[u]+path[u][j]);
            }
        }
    }
}
 

2 prim演算法

計算最小生成樹採用prim演算法。在每一步，將節點當做根並往上加邊，將相關頂點增加到增長的樹上。在演算法的每一個階段都可以通過選擇邊（u,v）,使得（u,v）的值是所有u在樹上但v不在樹上的邊的值的最小者，從而找到一個新的頂點並將它新增到這棵樹中。

程式碼如下：

void prim(const vector<vector<int>>& path, vector<bool>& flag,vector<int>& res,int v)
{
    const int n=flag.size();
    for(int i=0;i<n;++i)
    {
        res[i]=path[v][i];
    }
    flag[v]=true;
    for(int i=0;i<n;++i)
    {
        int u=-1;
        int tmp=maxint;//const int maxint=INT_MAX;
        for(int j=0;j<n;++j)
        {
            if(!flag[j]&&res[j]<tmp)
            {
                u=j;
                tmp=res[j];
            }
        }
        flag[u]=true;
        for(int j=0;j<n;++j)
        {
            if(!flag[j]&&path[u][j]!=maxint)
            {
                res[j]=min(res[j],path[u][j]);
            }
        }
    }
}
 

3 kruskal演算法

和prim演算法類似，每次都是尋找權值最短的一條邊。可以這樣看：開始存在n顆單節點樹，每次找到權值最短的一棵樹將其合併起來，但是注意不要形成環。最後只剩下一棵樹的時候，代表合併完成。

程式碼如下：

bool cmp(pair<pair<int,int>,int> a,pair<pair<int,int>,int> b)
{
    return a.second<=b.second;
}
bool isSame(vector<pair<pair<int,int>,bool>>& flag,pair<int,int> t)
{
    int x=t.first;
    int y=t.second;
    for(int i=x+1;i<y;++i)
    {
        if(flag.find(make_pair<make_pair(x,i),true>)!=flag.end()&&flag.find(make_pair<make_pair(i,y),true>)!=flag.end())
        {
            return true;
        }
    }
    return false;
}
void krustral(const vector<vector<int>>& path,vector<pair<pair<int,int>,bool>>& flag,vector<int>& res)
{
    const int n=flag.size();
    vector<pair<pair<int,int>,int>> m;
    for(int i=0;i<n;++i)
    {
        for(int j=i+1;j<n;++j)
        {
            if(path[i][j]!=maxint)
            {
                m.push_back(make_pair(make_pair(i,j),path[i][j]));
               // flag.push_back(make_pair(make_pair(i,j),false));
            }
        }
    }
    sort(m.begin(),m.end(),cmp);
    int count=0;
    for(int i=0;i<m.size();++i)
    {
        if(!isSame(flag,m[i].first))
        {
            res.push_back(m[i].second);
            flag.push_back(make_pair(m[i].first,true));
            ++count;
            if(count==n)
                return;
        }
    }
    
}