二叉樹,B-樹,B+樹,紅黑樹,LSM樹,AVL樹,堆
二叉樹的概念
在計算機領域,二叉樹是每個節點最多有兩個子樹的結構。通常子樹被稱為左子樹和右子樹。
二叉樹的特例:
滿二叉樹
滿二叉樹是完全二叉樹的特例。
- 所有葉節點必須在同一層上
- 除了葉子節點的所有節點都有兩個子節點
完全二叉樹
完全二叉樹可以看成是滿二叉樹的最後一行右側部分連續缺失。(最大堆和最小堆就是完全二叉樹)
平衡二叉樹
對於任何一個節點,左樹和右樹的絕對值差不超過1
二叉樹遍歷
二叉樹的遍歷主要有深度優先和廣度優先兩種。深度優先又包含前序遍歷,中序遍歷和後序遍歷。個有個的應用場景
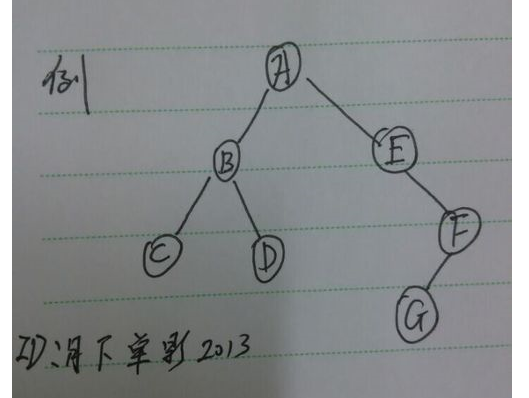
以如下例子說明
前序遍歷
首先遍歷根節點,然後是根節點的左側節點,然後繼續遍歷左側節點的左側節點,…一直到最左邊的葉節點。然後後退一層,訪問右節點,然後繼續後退一層。
簡單來說就是先根節點,然後左節點,最後右節點。
A B C D E F G
除了採用遞迴的辦法,前序遍歷還可以使用棧實現。
- 訪問結點P,並將結點P入棧;
- 判斷結點P的左孩子是否為空,若為空,則取棧頂結點並進行出棧操作,並將棧頂結點的右孩子置為當前的結點P,迴圈至1);若不為空,則將P的左孩子置為當前的結點P;
- 直到P為NULL並且棧為空,則遍歷結束。
中序遍歷
從根節點開始找,如果根節點有左側節點,就將尋找的指標向左側移動。
首先是左節點,然後是根節點,最後是右節點
其實反過來更好理解。如果有下列兩者之一情況,任何一個右節點都不能被遍歷
- 對應父節點沒有被遍歷
- 對應的左節點沒有被遍歷
C B D A E G F
注意,如果有多個節點符合被遍歷的條件,離最後一個遍歷點最近的點先被遍歷。
非遞迴實現方法如下
- 對於節點P,若其左孩子不為空,則將P入棧並將P的左孩子置為當前的P,然後對當前結點P再進行相同的處理;
- 若其左孩子為空,則取棧頂元素並進行出棧操作,訪問該棧頂結點,然後將當前的P置為棧頂結點的右孩子;
- 直到P為NULL並且棧為空則遍歷結束。
二叉查詢樹的中序遍歷就是一個遞增序列
後序遍歷
首先是左節點,然後是右節點,最後是根節點
和上面的道理類似。
C D B G F E A
後續遍歷的非遞迴實現是最複雜的。
對於任一結點P,將其入棧,然後沿其左子樹一直往下搜尋,直到搜尋到沒有左孩子的結點,此時該結點出現在棧頂,但是此時不能將其出棧並訪問, 因此其右孩子還為被訪問。所以接下來按照相同的規則對其右子樹進行相同的處理,當訪問完其右孩子時,該結點又出現在棧頂,此時可以將其出棧並訪問。這樣就 保證了正確的訪問順序。可以看出,在這個過程中,每個結點都兩次出現在棧頂,只有在第二次出現在棧頂時,才能訪問它。因此需要多設定一個變數標識該結點是 否是第一次出現在棧頂。
後序遍歷保證在操作某個節點時,肯定已經操作過其兩個子節點,可以用於二叉樹的節點刪除
廣度優先遍歷
廣度優先遍歷也被成為層次遍歷,使用佇列實現。
- 從佇列頭取出節點P,訪問節點P,如果其有子節點,將左節點和右節點先後入隊。
廣度優先遍歷常被用於序列化二叉樹,優點是不需要讀取完整序列就可以開始重構過程。
B-樹
首先明確一點,B-樹不讀做B減樹。中間的是連字元。這個B代表平衡的意思,但是B-樹不是平衡二叉樹。
B-tree被成為多路查詢樹,相對於二叉樹,B-tree更加矮胖。這樣做的原因是因為物理實現磁碟IO限制,矮胖有助於減少磁碟讀取索引的io次數。
B+樹
B+樹在B-樹的基礎上,限制所有資料必須儲存在葉節點,這樣之後,就可以為葉節點新增一個連結串列。這讓我門按照索引進行快速範圍讀取更加容易。
- mysql InnoDB引擎使用B+樹作為預設索引
B*樹
增加了只想相鄰兄弟節點的指標。
這是為了樹的分裂的需要。當一個節點滿後,B+樹會訪問自己的父節點,然後在父節點上新建一個與自己相鄰子節點,最後將自己的一半資料轉移到新節點上。
B*樹則不會優先創在新節點。利用自己指向兄弟節點的指標,他會首先嚐試將自己的資料轉移到自己的兄弟節點上。於是,他對樹空間利用率較高。
- B*是oracle中最長用到的索引
二叉搜尋樹
(1)若左子樹非空,則左子樹的所有節點小於他的根節點
(2)若右子樹非空,則右子樹的所有節點大於他的根節點
(3)左右子樹也都是二叉排序樹
顯然排序二叉樹可以用作排序,也可以用作快速查詢和插入。一般來講排序演算法的時間複雜度為Nlog2N
查詢演算法的時間複雜度為log2N
最大堆和最小堆
最大堆最小堆是完全二叉樹,所以底層可以採用陣列實現。
最大堆和最小堆常用語實現優先佇列。
最大堆和最小堆用於堆排序。
AVL樹
自平衡二叉查詢樹。查詢、插入和刪除在平均和最壞情況下都是O(logn)。增加和刪除可能需要通過一次或多次樹旋轉來重新平衡這個樹。在AVL樹中任何節點的兩個子樹的高度最大差別為一,所以它也被稱為高度平衡樹。
紅黑樹(RBTree)
紅黑樹是每個節點都帶有顏色屬性的二叉查詢樹,顏色或紅色或黑色。在二叉查詢樹強制一般要求以外,對於任何有效的紅黑樹我們增加了如下的額外要求:
- 節點是紅色或黑色。
- 根節點是黑色。
- 每個葉節點(NIL節點,空節點)是黑色的。
- 每個紅色節點的兩個子節點都是黑色。(從每個葉子到根的所有路徑上不能有兩個連續的紅色節點)
- 從任一節點到其每個葉子的所有路徑都包含相同數目的黑色節點。
適用於資料量小的需要排序的資料集(樹的高度比較高,資料量過大需要頻繁讀取磁碟)
- linux內部epoll的實現
- java中的TreeMap和TreeSet
AVL樹和RBT的比較
-
如果插入一個node引起了樹的不平衡,AVL和RB-Tree都是最多隻需要2次旋轉操作,即兩者都是O(1);但是在刪除node引起樹的不平衡時,最壞情況下,AVL需要維護從被刪node到root這條路徑上所有node的平衡性,因此需要旋轉的量級O(logN),而RB-Tree最多隻需3次旋轉,只需要O(1)的複雜度。
-
其次,AVL的結構相較RB-Tree來說更為平衡,在插入和刪除node更容易引起Tree的unbalance,因此在大量資料需要插入或者刪除時,AVL需要rebalance的頻率會更高。因此,RB-Tree在需要大量插入和刪除node的場景下,效率更高。自然,由於AVL高度平衡,因此AVL的search效率更高。
-
map的實現只是折衷了兩者在search、insert以及delete下的效率。總體來說,RB-tree的統計效能是高於AVL的。
LSM樹
日誌結構的合併樹(LSM-tree)是一種基於硬碟的資料結構,與B-tree相比,能顯著地減少硬碟磁碟臂的開銷,並能在較長的時間提供對檔案的高速插入(刪除)。然而LSM-tree在某些情況下,特別是在查詢需要快速響應時效能不佳。通常LSM-tree適用於索引插入比檢索更頻繁的應用系統。
HBase和RocksDB都採用了這種實際,在犧牲讀效能的前提下增加了寫入效能。

相關推薦
28、輸入兩棵二叉樹A,B,判斷B是不是A的子結構。(ps:我們約定空樹不是任意一個樹的子結構)
eno 技術分享 進行 結構 一個點 left courier mage new 題目描述 輸入兩棵二叉樹A,B,判斷B是不是A的子結構。(ps:我們約定空樹不是任意一個樹的子結構) 思路: 1、當Tree1和Tree2都不為零的時候,才進行比較。否則直接返回fals
整數對A滿足二叉查找樹,B滿足最大堆
構造 net [0 n) str delete enter 大神 code 1 題目 給出一組整數對 { (a[0], b[0]), (a[1], b[1]) ... (a[n-1], b[n-1]) },全部 a 值和 b 值分別不反
二叉樹,平衡二叉樹,紅黑樹,B-樹、B+樹、B*樹的區別
二叉查詢/搜尋/排序樹 BST (binary search/sort tree) 或者是一棵空樹; 或者是具有下列性質的二叉樹: (1)若它的左子樹不空,則左子樹上所有結點的值均小於它的根節點的值; (2)若它的右子樹上所有結點的值均大於它的根節點的值; (3)它的左、右子
假設二叉樹中每個結點的值為單個字元, 設計一個演算法將一棵以二叉鏈方式儲存的二叉樹 b 轉換成對應的順序儲存結構 a。——含具體實現工程
假設二叉樹中每個結點的值為單個字元, 設計一個演算法將一棵以二叉鏈方式儲存的二叉樹 b 轉換成對應的順序儲存結構 a。——李春葆資料結構第五版第七章,P246,第十題 思路解析: 解:設二叉樹的順序儲存結構型別為SqBTree,先將順序儲存結構a中所有元素置為‘#’(表示空結點)。將b轉
資料結構期末複習知識查漏補缺並配(帶詳解的)查漏習題(B樹,雜湊(雜湊),平衡二叉樹,KMP)
一.B樹(也叫B-)與B+樹專題 (1)B樹 重點總結: 1.結點最大的孩子數目稱為B樹的階。所以,2-3樹是3階B樹,2-3-4樹是3階B樹 2.所有葉節點位於同一層次 3. 4.,一般均是升序或降序 5.在B樹上查詢的過程是一個順指標查詢結點和在
整數對A滿足二叉查詢樹,B滿足最大堆
1 題目 給出一組整數對 { (a[0], b[0]), (a[1], b[1]) ... (a[n-1], b[n-1]) },所有 a 值和 b 值分別不重複(任意 i != j 滿足 a[i] != a[j] 且 b[i] != b[j])。構造一棵 n 結點的二叉樹,將這 n 個整數
【資料結構之二叉樹】(一)B樹、B-樹、B+樹、B*樹介紹,和B+樹更適合做檔案索引的原因
今天看資料庫,書中提到:由於索引是採用 B 樹結構儲存的,所以對應的索引項並不會被刪除,經過一段時間的增刪改操作後,資料庫中就會出現大量的儲存碎片,這和磁碟碎片、記憶體碎片產生原理是類似的,這些儲存碎片不僅佔用了儲存空間,而且降低了資料庫執行的速度。如果發現索引
二叉樹,完全二叉樹,滿二叉樹,二叉排序樹,平衡二叉樹,紅黑樹,B數,B-樹,B+樹,B*樹(一)
二叉樹 二叉樹:二叉樹是每個節點最多有兩個子樹的樹結構; 是n(n>=0)個結點的有限集合,它或者是空樹(n=0),或者是由一個根結點及兩顆互不相交的、分別稱為左子樹和右子樹的二叉樹所組成。 完全二叉樹 完全二叉樹:除最後一層外,每一層上的結點數均達到最
二叉樹,完全二叉樹,滿二叉樹,二叉排序樹,平衡二叉樹,紅黑樹,B數,B-樹,B+樹,B*樹(二)
二叉樹,完全二叉樹,滿二叉樹,二叉排序樹,平衡二叉樹,紅黑樹,B數,B-樹,B+樹,B*樹(一): BST樹 即二叉搜尋樹: 1.所有非葉子結點至多擁有兩個兒子(Left和Right); 2.所有結點儲存一個關鍵字;
終於搞懂了什麼是二叉查詢樹,AVL樹,B樹,B+樹,紅黑樹
二叉查詢樹: 二叉查詢樹就是左結點小於根節點,右結點大於根節點的一種排序樹,也叫二叉搜尋樹。也叫BST,英文Binary Sort Tree。 二叉查詢樹比普通樹查詢更快,查詢、插入、刪除的時間複雜度為O(logN)。但是二叉查詢樹有一種極端的情況,就是會變成一種線性連結
二叉查詢樹,紅黑樹,AVL樹,B~/B+樹(B-tree),伸展樹——優缺點及比較
二叉查詢樹(Binary Search Tree) 很顯然,二叉查詢樹的發現完全是因為靜態查詢結構在動態插入,刪除結點所表現出來的無能為力(需要付出極大的代價)。 BST 的操作代價分析: (1) 查詢代價: 任何一個數據的查詢過程都需要從根結點出發,沿
二叉樹之一BST樹,AVL樹詳解及B樹和紅黑樹原理分析
BST樹,AVL樹詳解及B樹和紅黑樹原理分析 網際網路面試中樹尤其是BST,AVL是提問的重點也是難點,甚至B樹乃至高階資料結構紅黑樹都是提問的重點,像阿里雲面試就曾經問過map實現機制(紅黑樹)及其原理,這裡我們要做到對BST/AVL完全熟悉能給出全部程式碼實現,紅黑樹、
哈夫曼編碼(基於哈夫曼樹-最優二叉樹,不唯一)、B樹(b-樹)、B+樹
整合自: http://blog.csdn.net/shuangde800/article/details/7341289 http://www.cnblogs.com/Jezze/archive/2011/12/23/2299884.html http:/
二叉查詢樹(BST),平衡二叉查詢樹(AVL),紅黑樹(RBT),B~/B+樹(B-tree)的比較
http://www.iteye.com/topic/614070 此少俠總結的特棒,直接收藏了。 我們這個專題介紹的動態查詢樹主要有: 二叉查詢樹(BST),平衡二叉查詢樹(AVL),紅黑樹(RBT),B~/B+樹(B-tree)。這四種樹都具備下面幾個優勢: (1) 都
二叉樹,B-樹,B+樹,紅黑樹,LSM樹,AVL樹,堆
二叉樹的概念 在計算機領域,二叉樹是每個節點最多有兩個子樹的結構。通常子樹被稱為左子樹和右子樹。 二叉樹的特例: 滿二叉樹 滿二叉樹是完全二叉樹的特例。 所有葉節點必須在同一層上 除了葉子節點的所有節點都有兩個子節點 完全二叉樹 完全二叉樹可以看成是滿二叉樹
輸入兩棵二叉樹A,B,判斷B是不是A的子結構。
要查詢樹A中是否存在和樹B結構一樣的子樹。我們可以分為兩步: 第一步在樹A中找到和B的根節點一樣的值一樣的結點R,第二步在判斷樹A中以R為根節點的子樹是不是包含和樹B一樣的結構。 樹的結點: struct TreeNode { int val;
淺談樹形結構的特性和應用(上):多叉樹,紅黑樹,堆,Trie樹,B樹,B+樹...
 上篇文章我們主要介紹了線性資料結構,本篇
二叉樹節點個數,葉子個數,第K層個數,最低公共節點
fun ret tco left right amp 最小公共 last turn 1. 節點個數 function getNodeNum(root){ if(root == null){ return 0; } //+1為root
給定有序數組,創建高度最小的二叉查找樹
enter reat 技術 二叉查找樹 treenode ret new t pre 有序數組 TreeNode createMinimalBST(int arr[], int start, int end) { if (end < start) { r
給定一個二叉樹,獲取該二叉樹的寬度深度
prototype %d param unsigned right idt height push signed 題目: Description 給定一個二叉樹,獲取該二叉樹的寬度深度。 Prototype int GetBiNo