寫這篇文章是因為面試時經常會問這個問題，但是工作中也沒用到過，所以一直是一知半解。但是我是屬於比較較真的人，這次下定決心要把它們搞明白。知識在於積累，多點知識對自己總是有好處的。

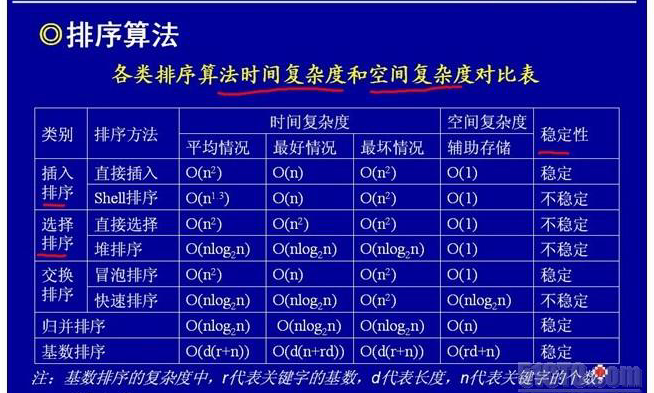
我比較好奇的是，這幾種方法到底哪個最快？我以前只知道氣泡排序，但這種方式可能是最慢的了。在網上搜了搜找到了這麼一張圖，看似蠻有道理的，如下：

從這個圖可以看出貌似堆排序和歸併排序最快因為無論好壞情況都是O（n * log 2 n），但我在實踐中則不然。

隨機不重複的整數

我們選擇10000個隨機不重複整數，可以看出快速排序是最快的，並且是經過多次實驗，名副其實，呵呵，它甚至比系統自帶的Arrays.sot（）都快，所以還是實踐出真知。

有序不重複整數

相反我們可以選擇一萬有個序不重複整數測試，插入排序  的英文最快的，而快速排序就不是最快的了，因為在有序中快速排序效果是很差的但不是最差的。測試結果如下圖：

系統排序Arrays.sort（）

Java Arrays中提供了對所有型別的排序。其中主要分為Primitive（8種基本型別）和Object兩大類。
基本型別：採用調優的快速排序;
物件型別：採用改進的歸併排序。

Java對Primitive（int，float等原型資料）陣列採用快速排序，物件物件陣列採用歸併排序。對這一區別，sun在<< Java教程>>中做出的解釋如下：

      原始碼中的快速排序，主要做了以下幾個方面的優化：
1）當待排序的陣列中的元素個數較少時，原始碼中的閥值為7，採用的是插入排序。儘管插入排序的時間複雜度為0（n ^ 2），但是當陣列元素較少時，插入排序優於快速排序，因為這時快速排序的遞迴操作影響效能
.2）較好的選擇了劃分元（基準元素） 。能夠將陣列分成大致兩個相等的部分，避免出現最壞的情況。例如當陣列有序的的情況下，選擇第一個元素作為劃分元，將使得演算法的時間複雜度達到為O（n ^ 2）。

原始碼中選擇劃分元的方法：
當陣列大小為size = 7時，取陣列中間元素作為劃分元.int n = m >> 1;（此方法值得借鑑）
當陣列大小7 <size <= 40時，取首，中，末三個元素中間大小的元素作為劃分元。
當陣列大小> 40時，從待排陣列中較均勻的選擇9個元素，選出一箇中中做做為分分元。

各種排序演算法並且有對應的舞蹈，太有創意了，哈哈。

舞蹈之快速排序：http：//v.youku.com/v_show/id_XMzMyODk4NTQ4.html？from = s1.8-1-1.2

舞蹈之氣泡排序：http：//v.youku.com/v_show/id_XMzMyOTAyMzQ0.html？from = s1.8-1-1.2

舞蹈之歸併排序：http：//v.youku.com/v_show/id_XMzMyODk5Njg4.html？from = s1.8-1-1.2

舞蹈之希爾排序：http：//v.youku.com/v_show/id_XMzMyODk5MzI4.html？from = s1.8-1-1.2

舞蹈之選擇排序：http：//v.youku.com/v_show/id_XMzMyODk5MDI0.html？from = s1.8-1-1.2

舞蹈之插入排序：http：//v.youku.com/v_show/id_XMzMyODk3NjI4.html？from = s1.8-1-1.2

冒泡排序演算法：

public	BubbleSort(Integer ar[]){
	Integer a[]=ar.clone();
	 long currentTime=System.currentTimeMillis();
	int temp=0;
	for(int i=0;i<a.length-1;i++){
		for(int j=0;j<a.length-1-i;j++){
		if(a[j]>a[j+1]){
			temp=a[j];
			a[j]=a[j+1];
			a[j+1]=temp;
		}
		}
	}
		
	long nowTime=System.currentTimeMillis();
	System.out.println("BubbleSort-----------cost time:"+(nowTime-currentTime));	
//	System.out.println(Arrays.toString( a));
}
}

快速排序演算法：

public class QuickSort {
	public	QuickSort(Integer ar[]){
		Integer a[]=ar.clone();
		long currentTime=System.currentTimeMillis();
		quick(a);
		long nowTime=System.currentTimeMillis();
		System.out.println("QuickSort-----------cost time:"+(nowTime-currentTime));
//		System.out.println(Arrays.toString( a));	
	}
	public int getMiddle(Integer[] list, int low, int high) {   
		        int tmp = list[low];    //陣列的第一個作為中軸   
		        while (low < high) {   
		            while (low < high && list[high] >= tmp) {   

	      high--;   
		            }   
		            list[low] = list[high];   //比中軸小的記錄移到低端   
		            while (low < high && list[low] <= tmp) {   
		                low++;   
		            }   
		            list[high] = list[low];   //比中軸大的記錄移到高階   
		        }   
	           list[low] = tmp;              //中軸記錄到尾   
		        return low;                   //返回中軸的位置   
		    }  
	public void _quickSort(Integer[] list, int low, int high) {   
		        if (low < high) {   
		           int middle = getMiddle(list, low, high);  //將list陣列進行一分為二   
		            _quickSort(list, low, middle - 1);        //對低字表進行遞迴排序   
		           _quickSort(list, middle + 1, high);       //對高字表進行遞迴排序   
		        }   
		    } 
	public void quick(Integer[] a2) {   
		        if (a2.length > 0) {    //檢視陣列是否為空   
		            _quickSort(a2, 0, a2.length - 1);   
	        }   
		   } 
	}

堆排序演算法：

public class HeapSort {
	public  HeapSort(Integer ar[]){
		Integer a[]=ar.clone();
		long currentTime=System.currentTimeMillis();
		heapSort(a);
		long nowTime=System.currentTimeMillis();
		System.out.println("HeapSort-----------cost time:"+(nowTime-currentTime));
//		System.out.println(Arrays.toString( a));
	}
	public  void heapSort(Integer[] a){
        int arrayLength=a.length;
        //迴圈建堆
        for(int i=0;i<arrayLength-1;i++){
            //建堆

      buildMaxHeap(a,arrayLength-1-i);
            //交換堆頂和最後一個元素
            swap(a,0,arrayLength-1-i);
           
        }
    }

    private  void swap(Integer[] data, int i, int j) {
        // TODO Auto-generated method stub
        int tmp=data[i];
        data[i]=data[j];
        data[j]=tmp;
    }
    //對data陣列從0到lastIndex建大頂堆
    private void buildMaxHeap(Integer[] data, int lastIndex) {
        // TODO Auto-generated method stub
        //從lastIndex處節點（最後一個節點）的父節點開始
        for(int i=(lastIndex-1)/2;i>=0;i--){
            //k儲存正在判斷的節點
            int k=i;
            //如果當前k節點的子節點存在
            while(k*2+1<=lastIndex){
                //k節點的左子節點的索引
                int biggerIndex=2*k+1;
                //如果biggerIndex小於lastIndex，即biggerIndex+1代表的k節點的右子節點存在
                if(biggerIndex<lastIndex){
                    //若果右子節點的值較大
                    if(data[biggerIndex]<data[biggerIndex+1]){
                        //biggerIndex總是記錄較大子節點的索引
                        biggerIndex++;
                    }
                }
                //如果k節點的值小於其較大的子節點的值
                if(data[k]<data[biggerIndex]){
                    //交換他們
                    swap(data,k,biggerIndex);
                    //將biggerIndex賦予k，開始while迴圈的下一次迴圈，重新保證k節點的值大於其左右子節點的值
                    k=biggerIndex;
                }else{
                    break;
                }
            }
           }
        }
     }

插入排序演算法：

public class InsertSort {
public InsertSort(Integer ar[]){
	Integer a[]=ar.clone();
	long currentTime=System.currentTimeMillis();
   int temp=0;
   for(int i=1;i<a.length;i++){
      int j=i-1;
      temp=a[i];
      for(;j>=0&&temp<a[j];j--){
      a[j+1]=a[j];                       //將大於temp的值整體後移一個單位
      }
      a[j+1]=temp;
   }
   long nowTime=System.currentTimeMillis();
	System.out.println("InsertSort-----------cost time:"+(nowTime-currentTime));
//	System.out.println(Arrays.toString( a));	
}
}

合併排序演算法：

public class MergeSort {
public	MergeSort(Integer ar[]){
	Integer a[]=ar.clone();
	long currentTime=System.currentTimeMillis();
	sort(a,0,a.length-1);
	long nowTime=System.currentTimeMillis();
	System.out.println("MergeSort-----------cost time:"+(nowTime-currentTime));
//	System.out.println(Arrays.toString( a));	
}
public void sort(Integer[] data, int left, int right) {
    // TODO Auto-generated method stub
    if(left<right){
        //找出中間索引
        int center=(left+right)/2;
        //對左邊陣列進行遞迴
        sort(data,left,center);
        //對右邊陣列進行遞迴
        sort(data,center+1,right);
        //合併
        merge(data,left,center,right);
        
    }
}
public void merge(Integer[] data, int left, int center, int right) {
    // TODO Auto-generated method stub
    int [] tmpArr=new int[data.length];
    int mid=center+1;
    //third記錄中間陣列的索引
    int third=left;
    int tmp=left;
    while(left<=center&&mid<=right){

   //從兩個陣列中取出最小的放入中間陣列
        if(data[left]<=data[mid]){
            tmpArr[third++]=data[left++];
        }else{
            tmpArr[third++]=data[mid++];
        }
    }
    //剩餘部分依次放入中間陣列
    while(mid<=right){
        tmpArr[third++]=data[mid++];
    }
    while(left<=center){
        tmpArr[third++]=data[left++];
    }
    //將中間陣列中的內容複製回原陣列
    while(tmp<=right){
        data[tmp]=tmpArr[tmp++];
    }
}

}

基排序演算法：

public RadixSort(Integer ar[]){
	Integer a[]=ar.clone();
	long currentTime=System.currentTimeMillis();
	sort(a);
	long nowTime=System.currentTimeMillis();
	System.out.println("RadixSort-----------cost time:"+(nowTime-currentTime));
//	System.out.println(Arrays.toString( a));	
}
public  void sort(Integer[] array){   
	           
	        //首先確定排序的趟數;   
        int max=array[0];   
        for(int i=1;i<array.length;i++){   
	           if(array[i]>max){   
               max=array[i];   
	           }   
	        }   

    int time=0;   
	       //判斷位數;   
	        while(max>0){   
	           max/=10;   
	            time++;   
	        }   
	           
        //建立10個佇列;   
	        List<List> queue=new ArrayList<List>();   
	        for(int i=0;i<10;i++){   
	        	ArrayList<Integer> queue1=new ArrayList<Integer>(); 
	            queue.add(queue1);   
        }   
	          
	        //進行time次分配和收集;   
	        for(int i=0;i<time;i++){   
	               
	            //分配陣列元素;   
	           for(int j=0;j<array.length;j++){   
	                //得到數字的第time+1位數; 
	        	   int x=array[j]%(int)Math.pow(10, i+1)/(int)Math.pow(10, i);
	        	   ArrayList<Integer> queue2=(ArrayList<Integer>) queue.get(x);
	        	   queue2.add(array[j]);
	        	   queue.set(x, queue2);
            }   
	            int count=0;//元素計數器;   
            //收集佇列元素;   
	            for(int k=0;k<10;k++){ 
                while(queue.get(k).size()>0){
                	ArrayList<Integer> queue3=(ArrayList<Integer>) queue.get(k);
	                    array[count]=queue3.get(0);   
	                    queue3.remove(0);
                    count++;
              }   
            }   
	}             
   }  

}

選擇排序演算法：

public class SelectSort {
	public SelectSort(Integer ar[]){
		Integer a[]=ar.clone();
		long currentTime=System.currentTimeMillis();
		int position=0;
		for(int i=0;i<a.length;i++){
			
			int j=i+1;
			position=i;
			int temp=a[i];
			for(;j<a.length;j++){
			if(a[j]<temp){
				temp=a[j];
				position=j;
			}
			}
			a[position]=a[i];
			a[i]=temp;
		}
		long nowTime=System.currentTimeMillis();
		System.out.println("SelectSort-----------cost time:"+(nowTime-currentTime));
//		System.out.println(Arrays.toString( a));
	}
}

希爾排序演算法：

public class ShellSort {
public	ShellSort(Integer ar[]){
	Integer a[]=ar.clone();
	long currentTime=System.currentTimeMillis();
	double d1=a.length;
	int temp=0;
	while(true){
		d1= Math.ceil(d1/2);
		int d=(int) d1;
		for(int x=0;x<d;x++){
			for(int i=x+d;i<a.length;i+=d){
				int j=i-d;
				temp=a[i];
				for(;j>=0&&temp<a[j];j-=d){
				a[j+d]=a[j];
				}
				a[j+d]=temp;
			}
		}
		if(d==1)
			break;
	}
	long nowTime=System.currentTimeMillis();
	System.out.println("ShellSort-----------cost time:"+(nowTime-currentTime));
//	System.out.println(Arrays.toString( a));
}
}

下面主要是參考別人的一些文章講講快速排序，其它的大家可以自行搜尋。快速排序由於排序效率在同為O（N * logN）的的幾種排序方法中效率較高，因此經常被採用，再加上快速排序思想----分治法也確實實用，因此很多軟體公司的筆試面試，包括像騰訊，微軟等知名IT公司都喜歡考這個，還有大大小的程式方面的考試如軟考，考研中也常常出現快速排序的身影。

快速排序是CRAHoare於1962年提出的一種劃分交換排序。它採用了一種分治的策略，通常稱其為分治法（分而ConquerMethod）。

該方法的基本思想是：

1.先從數列中取出一個數作為基準數。

2.分割槽過程，將比這個數大的數全放到它的右邊，小於或等於它的數全放到它的左邊。

3.再對左右區間重複第二步，直到各區間只有一個數。

雖然快速排序稱為分治法，但分治法這三個字顯然無法很好的概括快速排序的全部步驟因此我的對快速排序作了進一步的說明：挖坑填數+分治法：

先來看例項吧，定義下面再給出（最好能用自己的話來總結定義，這樣對實現程式碼會有幫助）。

以一個數組作為示例，取區間第一個數為基準數

由於已經將a [0]中的數儲存到X中，可以理解成在陣列a [0]上挖了個坑，可以將其它資料填充到這來。初始時，i = 0; j = 9; X = a [i] = 72

從Ĵ開始向前找一個比X小或等於X的數。當J = 8，符合條件，將一個[8]挖出再填到上一個坑一個[0]中。一個[0] = A [ 8]; 我++; 這樣一個坑一個[0]就被搞定了，但又形成了一個新坑一個[8]，這怎麼辦了？簡單，再找數字來填一個[8]這個坑。這次從我開始向後找一個大於X的數，當I = 3，符合條件，將[3]挖出再填到上一個坑中一個[8] = [3]。j--;

陣列變為：

再重複上面的步驟，先從後向前找，再從前向後找 .i = 3; j = 7; X = 72

從j開始向前找，當j = 5，符合條件，將a [5]挖出填到上一個坑中，a [3] = a [5]; 我++;

從我開始向後找，當I = 5時，由於我==Ĵ退出。

此時，i = j = 5，而a [5]剛好又是上次挖的坑，因此將X填入a [5]。

陣列變為：

挖坑對填數進行總結可以看出一個[5]前面的數字都小於它，一個[5]後面的數字都大於它。因此再對一個[0 ... 4]和A [6 ... 9]這二區間個子重複上述步驟就可以了。

1.i = L; j = R; 將基準數挖出形成第一個坑一個[i]中。

2.j--由後向前找比它小的數，找到後挖出此數填前一個坑A [1]中。

3.I ++由前向後找比它大的數，找到後也挖出此數填到前一個坑一個[J]中。

4.再重複執行2,3-二步，直到我==Ĵ，將基準數填入一個[I]中。

照著這個總結很容易實現挖坑填數的程式碼：

int AdjustArray(int s[], int l, int r) //返回調整後基準數的位置
{
	int i = l, j = r;
	int x = s[l]; //s[l]即s[i]就是第一個坑
	while (i < j)
	{
		// 從右向左找小於x的數來填s[i]
		while(i < j && s[j] >= x) 
			j--;  
		if(i < j) 
		{
			s[i] = s[j]; //將s[j]填到s[i]中，s[j]就形成了一個新的坑
			i++;
		}

		// 從左向右找大於或等於x的數來填s[j]
		while(i < j && s[i] < x)
			i++;  
		if(i < j) 
		{
			s[j] = s[i]; //將s[i]填到s[j]中，s[i]就形成了一個新的坑
			j--;
		}
	}
	//退出時，i等於j。將x填到這個坑中。
	s[i] = x;

	return i;
}

再寫分治法的程式碼：

void quick_sort1(int s[], int l, int r)
{
	if (l < r)
    {
		int i = AdjustArray(s, l, r);//先成挖坑填數法調整s[]
		quick_sort1(s, l, i - 1); // 遞迴呼叫 
		quick_sort1(s, i + 1, r);
	}
}

這樣的程式碼顯然不夠簡潔，對其組合整理下

//快速排序
void quick_sort(int s[], int l, int r)
{
    if (l < r)
    {
		//Swap(s[l], s[(l + r) / 2]); //將中間的這個數和第一個數交換 參見注1
        int i = l, j = r, x = s[l];
        while (i < j)
        {
            while(i < j && s[j] >= x) // 從右向左找第一個小於x的數
				j--;  
            if(i < j) 
				s[i++] = s[j];
			
            while(i < j && s[i] < x) // 從左向右找第一個大於等於x的數
				i++;  
            if(i < j) 
				s[j--] = s[i];
        }
        s[i] = x;
        quick_sort(s, l, i - 1); // 遞迴呼叫 
        quick_sort(s, i + 1, r);
    }
}

下面是八種排序演算法比較實踐程式碼，大家可以下載執行研究一下。