使用Python進行描述性統計
2 使用NumPy和SciPy進行數值分析
2.1 基本概念
1 from numpy import array 2 from numpy.random import normal, randint 3 #使用List來創造一組資料 4 data = [1, 2, 3] 5 #使用ndarray來創造一組資料 6 data = array([1, 2, 3]) 7 #創造一組服從正態分佈的定量資料 8 data = normal(0, 10, size=10) 9 #創造一組服從均勻分佈的定性資料 10 data = randint(0, 10, size=10)
2.2 中心位置(均值、中位數、眾數)
資料的中心位置是我們最容易想到的資料特徵。藉由中心位置,我們可以知道資料的一個平均情況,如果要對新資料進行預測,那麼平均情況是非常直觀地選擇。資料的中心位置可分為均值(Mean),中位數(Median),眾數(Mode)。其中均值和中位數用於定量的資料,眾數用於定性的資料。
對於定量資料(Data)來說,均值是總和除以總量(N),中位數是數值大小位於中間(奇偶總量處理不同)的值:

均值相對中位數來說,包含的資訊量更大,但是容易受異常的影響。使用NumPy計算均值與中位數:
1 from numpy import mean, median2 3 #計算均值 4 mean(data) 5 #計算中位數 6 median(data)
對於定性資料來說,眾數是出現次數最多的值,使用SciPy計算眾數:
1 from scipy.stats import mode 2 3 #計算眾數 4 mode(data)
2.3 發散程度(極差、方差、標準差、變異係數)
對資料的中心位置有所瞭解以後,一般我們會想要知道資料以中心位置為標準有多發散。如果以中心位置來預測新資料,那麼發散程度決定了預測的準確性。資料的發散程度可用極差(PTP)、方差(Variance)、標準差(STD)、變異係數(CV)來衡量,它們的計算方法如下:

極差是隻考慮了最大值和最小值的發散程度指標,相對來說,方差包含了更多的資訊,標準差基於方差但是與原始資料同量級,變異係數基於標準差但是進行了無量綱處理。使用NumPy計算極差、方差、標準差和變異係數:
1 from numpy import mean, ptp, var, std 2 3 #極差 4 ptp(data) 5 #方差 6 var(data) 7 #標準差 8 std(data) 9 #變異係數 10 mean(data) / std(data)
2.4 偏差程度(z-分數)
之前提到均值容易受異常值影響,那麼如何衡量偏差,偏差到多少算異常是兩個必須要解決的問題。定義z-分數(Z-Score)為測量值距均值相差的標準差數目:
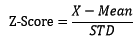
當標準差不為0且不為較接近於0的數時,z-分數是有意義的,使用NumPy計算z-分數:
1 from numpy import mean, std 2 3 #計算第一個值的z-分數 4 (data[0]-mean(data)) / std(data)
通常來說,z-分數的絕對值大於3將視為異常。
2.5 相關程度
有兩組資料時,我們關心這兩組資料是否相關,相關程度有多少。用協方差(COV)和相關係數(CORRCOEF)來衡量相關程度:
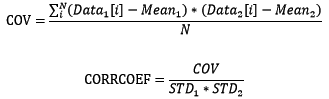
協方差的絕對值越大表示相關程度越大,協方差為正值表示正相關,負值為負相關,0為不相關。相關係數是基於協方差但進行了無量綱處理。使用NumPy計算協方差和相關係數:
1 from numpy import array, cov, corrcoef 2 3 data = array([data1, data2]) 4 5 #計算兩組數的協方差 6 #引數bias=1表示結果需要除以N,否則只計算了分子部分 7 #返回結果為矩陣,第i行第j列的資料表示第i組數與第j組數的協方差。對角線為方差 8 cov(data, bias=1) 9 10 #計算兩組數的相關係數 11 #返回結果為矩陣,第i行第j列的資料表示第i組數與第j組數的相關係數。對角線為1 12 corrcoef(data)
2.6 回顧
| 包 | 方法 | 說明 |
| numpy | array | 創造一組數 |
| numpy.random | normal | 創造一組服從正態分佈的定量數 |
| numpy.random | randint | 創造一組服從均勻分佈的定性數 |
| numpy | mean | 計算均值 |
| numpy | median | 計算中位數 |
| scipy.stats | mode | 計算眾數 |
| numpy | ptp | 計算極差 |
| numpy | var | 計算方差 |
| numpy | std | 計算標準差 |
| numpy | cov | 計算協方差 |
| numpy | corrcoef | 計算相關係數 |
3 使用Matplotlib進行圖分析
3.1 基本概念
使用圖分析可以更加直觀地展示資料的分佈(頻數分析)和關係(關係分析)。柱狀圖和餅形圖是對定性資料進行頻數分析的常用工具,使用前需將每一類的頻數計算出來。直方圖和累積曲線是對定量資料進行頻數分析的常用工具,直方圖對應密度函式而累積曲線對應分佈函式。散點圖可用來對兩組資料的關係進行描述。在沒有分析目標時,需要對資料進行探索性的分析,箱形圖將幫助我們完成這一任務。
在此,我們使用一組容量為10000的男學生身高,體重,成績資料來講解如何使用Matplotlib繪製以上圖形,建立資料的程式碼如下:

1 from numpy import array 2 from numpy.random import normal 3 4 def genData(): 5 heights = [] 6 weights = [] 7 grades = [] 8 N = 10000 9 10 for i in range(N): 11 while True: 12 #身高服從均值172,標準差為6的正態分佈 13 height = normal(172, 6) 14 if 0 < height: break 15 while True: 16 #體重由身高作為自變數的線性迴歸模型產生,誤差服從標準正態分佈 17 weight = (height - 80) * 0.7 + normal(0, 1) 18 if 0 < weight: break 19 while True: 20 #分數服從均值為70,標準差為15的正態分佈 21 score = normal(70, 15) 22 if 0 <= score and score <= 100: 23 grade = 'E' if score < 60 else ('D' if score < 70 else ('C' if score < 80 else ('B' if score < 90 else 'A'))) 24 break 25 heights.append(height) 26 weights.append(weight) 27 grades.append(grade) 28 return array(heights), array(weights), array(grades) 29 30 heights, weights, grades = genData()View Code
3.2 頻數分析
3.2.1 定性分析(柱狀圖、餅形圖)
柱狀圖是以柱的高度來指代某種型別的頻數,使用Matplotlib對成績這一定性變數繪製柱狀圖的程式碼如下:
1 from matplotlib import pyplot 2 3 #繪製柱狀圖 4 def drawBar(grades): 5 xticks = ['A', 'B', 'C', 'D', 'E'] 6 gradeGroup = {} 7 #對每一類成績進行頻數統計 8 for grade in grades: 9 gradeGroup[grade] = gradeGroup.get(grade, 0) + 1 10 #建立柱狀圖 11 #第一個引數為柱的橫座標 12 #第二個引數為柱的高度 13 #引數align為柱的對齊方式,以第一個引數為參考標準 14 pyplot.bar(range(5), [gradeGroup.get(xtick, 0) for xtick in xticks], align='center') 15 16 #設定柱的文字說明 17 #第一個引數為文字說明的橫座標 18 #第二個引數為文字說明的內容 19 pyplot.xticks(range(5), xticks) 20 21 #設定橫座標的文字說明 22 pyplot.xlabel('Grade') 23 #設定縱座標的文字說明 24 pyplot.ylabel('Frequency') 25 #設定標題 26 pyplot.title('Grades Of Male Students') 27 #繪圖 28 pyplot.show() 29 30 drawBar(grades)
繪製出來的柱狀圖的效果如下:
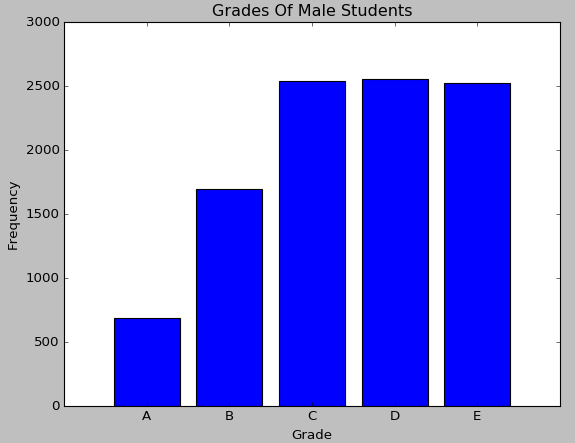
而餅形圖是以扇形的面積來指代某種型別的頻率,使用Matplotlib對成績這一定性變數繪製餅形圖的程式碼如下:
1 from matplotlib import pyplot 2 3 #繪製餅形圖 4 def drawPie(grades): 5 labels = ['A', 'B', 'C', 'D', 'E'] 6 gradeGroup = {} 7 for grade in grades: 8 gradeGroup[grade] = gradeGroup.get(grade, 0) + 1 9 #建立餅形圖 10 #第一個引數為扇形的面積 11 #labels引數為扇形的說明文字 12 #autopct引數為扇形佔比的顯示格式 13 pyplot.pie([gradeGroup.get(label, 0) for label in labels], labels=labels, autopct='%1.1f%%') 14 pyplot.title('Grades Of Male Students') 15 pyplot.show() 16 17 drawPie(grades)
繪製出來的餅形圖效果如下:

3.2.2 定量分析(直方圖、累積曲線)
直方圖類似於柱狀圖,是用柱的高度來指代頻數,不同的是其將定量資料劃分為若干連續的區間,在這些連續的區間上繪製柱。使用Matplotlib對身高這一定量變數繪製直方圖的程式碼如下:
1 from matplotlib import pyplot 2 3 #繪製直方圖 4 def drawHist(heights): 5 #建立直方圖 6 #第一個引數為待繪製的定量資料,不同於定性資料,這裡並沒有事先進行頻數統計 7 #第二個引數為劃分的區間個數 8 pyplot.hist(heights, 100) 9 pyplot.xlabel('Heights') 10 pyplot.ylabel('Frequency') 11 pyplot.title('Heights Of Male Students') 12 pyplot.show() 13 14 drawHist(heights)
直方圖對應資料的密度函式,由於身高變數是屬於服從正態分佈的,從繪製出來的直方圖上也可以直觀地看出來:
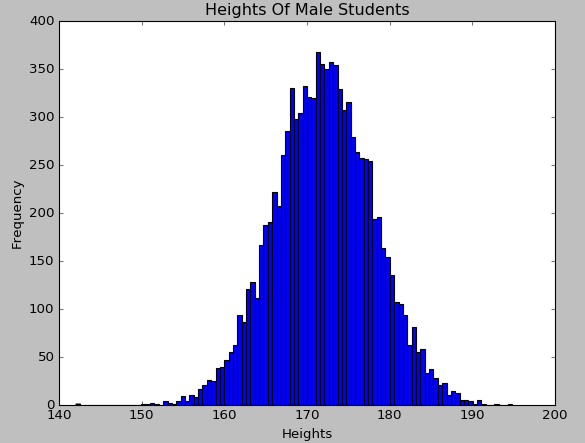
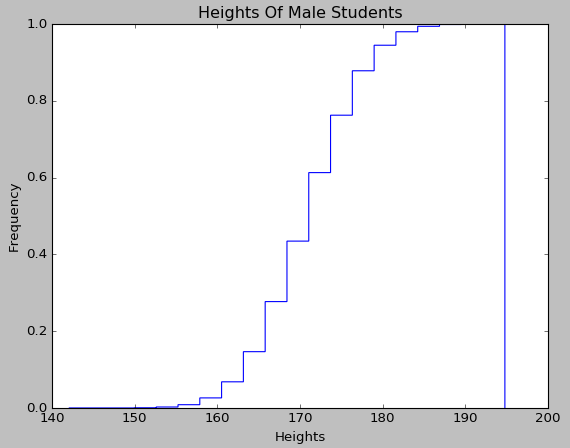
使用Matplotlib對身高這一定量變數繪製累積曲線的程式碼如下:
1 from matplotlib import pyplot 2 3 #繪製累積曲線 4 def drawCumulativeHist(heights): 5 #建立累積曲線 6 #第一個引數為待繪製的定量資料 7 #第二個引數為劃分的區間個數 8 #normed引數為是否無量綱化 9 #histtype引數為'step',繪製階梯狀的曲線 10 #cumulative引數為是否累積 11 pyplot.hist(heights, 20, normed=True, histtype='step', cumulative=True) 12 pyplot.xlabel('Heights') 13 pyplot.ylabel('Frequency') 14 pyplot.title('Heights Of Male Students') 15 pyplot.show() 16 17 drawCumulativeHist(heights)
累積曲線對應資料的分佈函式,由於身高變數是屬於服從正態分佈的,從繪製出來的累積曲線圖上也可以直觀地看出來:
3.3 關係分析(散點圖)
在散點圖中,分別以自變數和因變數作為橫縱座標。當自變數與因變數線性相關時,在散點圖中,點近似分佈在一條直線上。我們以身高作為自變數,體重作為因變數,討論身高對體重的影響。使用Matplotlib繪製散點圖的程式碼如下:
from matplotlib import pyplot #繪製散點圖 def drawScatter(heights, weights): #建立散點圖 #第一個引數為點的橫座標 #第二個引數為點的縱座標 pyplot.scatter(heights, weights) pyplot.xlabel('Heights') pyplot.ylabel('Weights') pyplot.title('Heights & Weights Of Male Students') pyplot.show() drawScatter(heights, weights)
我們在建立資料時,體重這一變數的確是由身高變數通過線性迴歸產生,繪製出來的散點圖如下:

3.4 探索分析(箱形圖)
在不明確資料分析的目標時,我們對資料進行一些探索性的分析,通過我們可以知道資料的中心位置,發散程度以及偏差程度。使用Matplotlib繪製關於身高的箱形圖的程式碼如下:
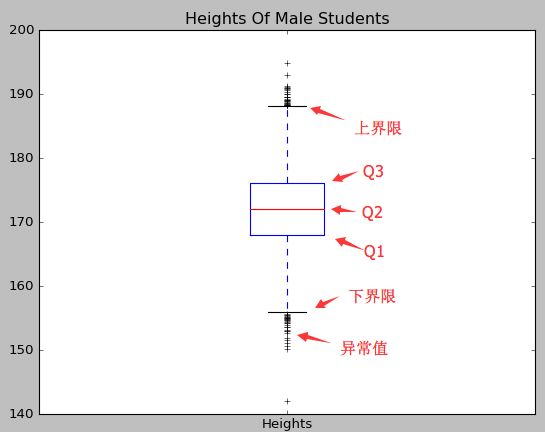
1 from matplotlib import pyplot 2 3 #繪製箱形圖 4 def drawBox(heights): 5 #建立箱形圖 6 #第一個引數為待繪製的定量資料 7 #第二個引數為資料的文字說明 8 pyplot.boxplot([heights], labels=['Heights']) 9 pyplot.title('Heights Of Male Students') 10 pyplot.show() 11 12 drawBox(heights)
繪製出來的箱形圖中,包含3種資訊:
- Q2所指的紅線為中位數
- Q1所指的藍框下側為下四分位數,Q3所指的藍框上側為上四分位數,Q3-Q1為四分為差。四分位差也是衡量資料的發散程度的指標之一。
- 上界線和下界線是距離中位數1.5倍四分位差的線,高於上界線或者低於下界線的資料為異常值。
3.5 回顧
| 方法 | 說明 |
| bar | 柱狀圖 |
| pie | 餅形圖 |
| hist | 直方圖&累積曲線 |
| scatter | 散點圖 |
| boxplot | 箱形圖 |
| xticks | 設定柱的文字說明 |
| xlabel | 橫座標的文字說明 |
| ylabel | 縱座標的文字說明 |
| title | 標題 |
| show | 繪圖 |
4 總結
描述性統計是容易操作,直觀簡潔的資料分析手段。但是由於簡單,對多元變數的關係難以描述。現實生活中,自變數通常是多元的:決定體重不僅有身高,還有飲食習慣,肥胖基因等等因素。通過一些高階的資料處理手段,我們可以對多元變數進行處理,例如特徵工程中,可以使用互資訊方法來選擇多個對因變數有較強相關性的自變數作為特徵,還可以使用主成分分析法來消除一些冗餘的自變數來降低運算複雜度。
5 參考資料
相關推薦
使用Python進行描述性統計
2 使用NumPy和SciPy進行數值分析 2.1 基本概念 1 from numpy import array 2 from numpy.random import normal, randint 3 #使用List來創造一組資料 4 data = [1, 2, 3] 5
利用Python進行數據分析_Pandas_匯總和計算描述統計
描述 行數 OS 進行 weight pytho col font gpo 申明:本系列文章是自己在學習《利用Python進行數據分析》這本書的過程中,為了方便後期自己鞏固知識而整理。利用Python進行數據分析_Pandas_匯總和計算描述統計
統計了一下員工的資訊!並用Python進行了的分析!這結果真尷尬!
從一個公司的在職員工資訊列表中,分析這個公司男女比例,員工的平均年齡,員工在公司的平均在職年限,以及各個年齡階段的人數,各個職級的男女人數。 不同的行業,同一個崗位,男女比例差異比較大。比如銷售,需要跑客戶,經常出差,還要和客戶吃飯喝酒,所以一般男銷售會多一些。但不是所有
24、python對資料框進行分組統計簡單操作
分組分析:是指根據分組欄位,將分析物件劃分成不同的部分,已進行對比分析各組之間的差異性的一種分析方法 常見的統計指標: 計數 求和 平均值 1 函式 01 分組統計函式: groupby(by=[分組列1,分組列2,...])[統計列1,統計列2,。。。] .agg({統計列名1:統計函
使用python進行描述型統計
1 描述性統計是什麼? 2 使用NumPy和SciPy進行數值分析 2.1 基本概念 2.2 中心位置(均值、中位數、眾數) 2.3 發散程度(極差,方差、標準差、變異係數) 2.4 偏差程度(z-分數) 2.5 相關程度(協方差,相關係數) 2.6 回顧 3 使用M
python描述性統計分析
1、 數值分析 from numpy import array from numpy.random import normal, randint list_data = [1, 2, 3] #使用List來創造一組資料 array_data = array([1, 2
用python進行統計分析
模組為我們提供了非常多的描述性統計分析的指標函式,如總和、均值、最小值、最大值等,我們來具體看看這些函式: 1、隨機生成三組資料 import numpy as np import pandas as pd np.random.seed(1234) d1
用Python對微信好友進行簡單統計分析,獲取好友的基本資訊!
早些日子有人問我我的微信裡面有一共多少朋友,我就隨後拉倒了通訊錄最下面就找到了微信一共有多少位好友。然後他又問我,這裡面你認識多少人?這一句話問的我很無語。一千多個好友我真的不知道認識的人有多少。他還緊追著不放了,你知道你微信朋友的男女比例嘛?你知道你微信朋友大部分來自什麼地方嗎? 不知道
用python學概率與統計(第二章)描述性統計:表格法,圖形法
頻數分佈 2.1彙總定性資料 柱狀圖 import numpy as np import pandas as pd from pandas import Series,DataFrame import matplotlib.pyplot as pl
Python進行文字預處理(文字分詞,過濾停用詞,詞頻統計,特徵選擇,文字表示)
系統:win7 32位 分詞軟體:PyNLPIR 整合開發環境(IDE):Pycharm 功能:實現多級文字預處理全過程,包括文字分詞,過濾停用詞,詞頻統計,特徵選擇,文字表示,並將結果匯出為WEKA能夠處理的.arff格式。 直接上程式碼: #!/usr/bin/
通過Python進行MySQL表資訊統計
導讀 在上一篇文章中簡單的介紹了使用python-mysql-replication 來解析 MySQL binlog來完成實時統計的業務,當然,在現實的業務中不可能用的那麼簡單的。 囉哩八說 今天的目的不是介紹真實的業務場景如何使用 python-mysql-replication,而是推出一枚&l
用Python進行網頁抓取
google 神奇 顯示 rss 遍歷 ecb data- 可用 appdata 引言 從網頁中提取信息的需求日益劇增,其重要性也越來越明顯。每隔幾周,我自己就想要到網頁上提取一些信息。比如上周我們考慮建立一個有關各種數據科學在線課程的歡迎程度和意見的索引。我們不僅需要
利用python進行數據分析——histogram
python hist()DataFrame.hist(data, column=None, by=None, grid=True, xlabelsize=None, xrot=None, ylabelsize=None, yrot=None,ax=None, sharex=False, sharey=Fal
Python進行數據分析之一:相關Package的安裝
ans 防止 log matplot 行數據 解釋 原型 簡單 下載 一、為什麽要使用Python進行數據分析? python擁有一個巨大的活躍的科學計算社區,擁有不斷改良的庫,能夠輕松的集成C,C++,Fortran代碼(Cython項目),可以同時用於研究和原型的構建以
python3 簡單實現從csv文件中讀取內容,並對內容進行分類統計
tmp spa writer ict 打開文件 while 類型 spl blog 新手python剛剛上路,在實際工作中遇到如題所示的問題,嘗試使用python3簡單實現如下,歡迎高手前來優化import csv #打開文件,用with打開可以不用去特意關閉file了
PYTHON學習(三)之利用python進行數據分析(1)---準備工作
-- 下載 rip 安裝包 png 要求 eight code 電腦 學習一門語言就是不斷實踐,python是目前用於數據分析最流行的語言,我最近買了本書《利用python進行數據分析》(Wes McKinney著),還去圖書館借了本《Python數據分析基礎教程--N
hive進行詞頻統計
exp 通過 zookeeper oracle bin 文件 create order lec 統計文件信息: $ /opt/cdh-5.3.6/hadoop-2.5.0/bin/hdfs dfs -text /user/hadoop/wordcount/input/wc
針對微信的一篇推送附有的數據鏈接進行MapReduce統計
全球 tco 大數據 cer 推送 xtend .get ati 適用於 原推送引用:https://mp.weixin.qq.com/s/3qQqN6qzQ3a8_Au2qfZnVg 版權歸原作者所有,如有侵權請及時聯系本人,見諒! 原文采用Excel進行統計數據,這
R語言實戰 - 基本統計分析(1)- 描述性統計分析
4.3 summary eas 方法 func -- 4.4 1.0 6.5 > vars <- c("mpg", "hp", "wt") > head(mtcars[vars]) mpg hp wt Maz
【學習】Python進行數據提取的方法總結【轉載】
多個 pandas flow cells nump 特定 blue 和數 index 鏈接:http://www.jb51.net/article/90946.htm 數據提取是分析師日常工作中經常遇到的需求。如某個用戶的貸款金額,某個月或季度的利息總收入,某個特定時間段的

