哈夫曼樹(最優二叉樹)的構造【二叉樹的應用】
對於給定一個長度為m序列,構造一顆以序列值為權的m個外部結點的擴充二叉樹,使得帶權的外部路徑長度WPL最小,就稱這顆擴充二叉樹為 哈夫曼(Huffman)樹(最優二叉樹)。構造Huffman Tree 的演算法也就是哈夫曼演算法。
演算法基本思想:
1)給定m個權值,首先構造m課擴充二叉樹,每顆只有一個外部結點(根結點)。
2)在已經構造的所有擴充二叉樹中,選擇根結點權值最小的和次小的兩顆,將它們作為左、右子樹,構造一顆新的擴充二叉樹,它的根結點的權值為其左右子樹根結點的權值之和。
3)重複2),每次使得擴充二叉樹的數目減一,當只剩下最後一顆擴充二叉樹時,其便是所求的哈夫曼樹。
程式碼實現:
#include <iostream> #define MAXINT 10000 #define N 13 //構建13個結點 using namespace std; struct HtNode{ int var,parent,llink,rlink; }; struct HtTree{ int m,root; //外部結點個數、根結點在ht陣列中的下標 struct HtNode *ht; }; typedef struct HtTree * PHtTree; void print(PHtTree p) { cout<<"index var parent lchild rchild\n"; for(int i=0;i<2*N-1;i++) cout<<i<<"\t"<<p->ht[i].var<<" "<<p->ht[i].parent<<" " <<p->ht[i].llink<<" "<<p->ht[i].rlink<<endl; } PHtTree huffman(int m,int *seq) { PHtTree pht=new struct HtTree; //分配空間 pht->ht=new HtNode[2*m-1]; //外部結點為m,則內部結點為m-1,則總共點數為2m-1 for(int i=0;i<2*m-1;i++){ //置ht陣列初態 pht->ht[i].llink=pht->ht[i].rlink=pht->ht[i].parent=-1; pht->ht[i].var= i<m?seq[i]:-1; } cout<<"陣列ht的初態:\n"; print(pht); for(int i=0;i<m-1;i++){ //每次迴圈構造一個內部結點 int m1=MAXINT,m2=MAXINT; int x1=-1,x2=-1; for(int j=0;j<m+i;j++){ //找最小權的無父節點的結點 if(pht->ht[j].var<m1 && pht->ht[j].parent==-1){ m2=m1;x2=x1; m1=pht->ht[j].var; x1=j; } //找次最小權的無父節點的結點 else if(pht->ht[j].var<m2 && pht->ht[j].parent==-1){ m2=pht->ht[j].var;x2=j; } } //構造內部結點 pht->ht[x1].parent=pht->ht[x2].parent=m+i; pht->ht[m+i].var=m1+m2; pht->ht[m+i].llink=x1; pht->ht[m+i].rlink=x2; } pht->root=2*m-2; return pht; } int main() { int sequence[N]; for(int i=0;i<N;i++) cin>>sequence[i]; PHtTree p=huffman(N,sequence); cout<<"陣列ht的終態:\n"; print(p); return 0; }
時間複雜度為O(n^2)。
Input
2 3 5 7 11 13 17 19 23 29 31 37 41Output
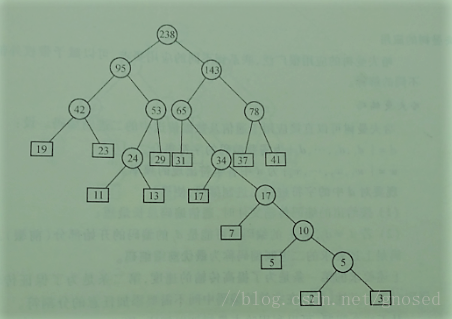
注意,結果中index表示陣列ht的下標,意味著各節點之間的關係,例如(下標為0的)結點2和(下標為1的)結點3的父節點(下標為13)為5,再看下標的13的結點5,它的左孩子是(下標為0的)結點2,右孩子為(下標為1的)結點3。陣列ht的初態: index var parent lchild rchild 0 2 -1 -1 -1 1 3 -1 -1 -1 2 5 -1 -1 -1 3 7 -1 -1 -1 4 11 -1 -1 -1 5 13 -1 -1 -1 6 17 -1 -1 -1 7 19 -1 -1 -1 8 23 -1 -1 -1 9 29 -1 -1 -1 10 31 -1 -1 -1 11 37 -1 -1 -1 12 41 -1 -1 -1 13 -1 -1 -1 -1 14 -1 -1 -1 -1 15 -1 -1 -1 -1 16 -1 -1 -1 -1 17 -1 -1 -1 -1 18 -1 -1 -1 -1 19 -1 -1 -1 -1 20 -1 -1 -1 -1 21 -1 -1 -1 -1 22 -1 -1 -1 -1 23 -1 -1 -1 -1 24 -1 -1 -1 -1 陣列ht的終態: index var parent lchild rchild 0 2 13 -1 -1 1 3 13 -1 -1 2 5 14 -1 -1 3 7 15 -1 -1 4 11 16 -1 -1 5 13 16 -1 -1 6 17 17 -1 -1 7 19 18 -1 -1 8 23 18 -1 -1 9 29 19 -1 -1 10 31 20 -1 -1 11 37 21 -1 -1 12 41 21 -1 -1 13 5 14 0 1 14 10 15 2 13 15 17 17 3 14 16 24 19 4 5 17 34 20 6 15 18 42 22 7 8 19 53 22 16 9 20 65 23 10 17 21 78 23 11 12 22 95 24 18 19 23 143 24 20 21 24 238 -1 22 23
構造的哈夫曼樹如下,
相關推薦
資料結構實驗之二叉樹六:哈夫曼編碼(最優二叉樹)
Problem Description 字元的編碼方式有多種,除了大家熟悉的ASCII編碼,哈夫曼編碼(Huffman Coding)也是一種編碼方式,它是可變字長編碼。該方法完全依據字元出現概率來構造出平均長度最短的編碼,稱之為最優編碼。哈夫曼編碼常被用於資
哈夫曼編碼效果最優的原因
首先了解幾個概念: 1.路徑長度 在樹中從一個結點到另一個結點所經歷的分支構成了這兩個結點間的路徑上的分支數稱為它的路徑長度 2.樹的路徑長度 樹的路徑長度是從樹根到樹中每一結點的路
哈夫曼編碼(基於哈夫曼樹-最優二叉樹,不唯一)、B樹(b-樹)、B+樹
整合自: http://blog.csdn.net/shuangde800/article/details/7341289 http://www.cnblogs.com/Jezze/archive/2011/12/23/2299884.html http:/
資料結構之哈夫曼樹(最優二叉樹)
文字壓縮是一種非常重要的技術,自然涉及到了壓縮編碼。哈夫曼編碼——一種最基本的壓縮編碼方法 幾個術語: 1、路徑:樹中兩個節點之間的分支序列 2、路徑長度:路徑上的分支數目
哈夫曼樹(最優二叉樹)的構造【二叉樹的應用】
對於給定一個長度為m序列,構造一顆以序列值為權的m個外部結點的擴充二叉樹,使得帶權的外部路徑長度WPL最小,就稱這顆擴充二叉樹為 哈夫曼(Huffman)樹(最優二叉樹)。構造Huffman Tree 的演算法也就是哈夫曼演算法。演算法基本思想:1)給定m個權
樹之哈夫曼樹(最優二叉樹)
本文來介紹哈夫曼樹。哈夫曼樹又叫最優二叉樹,是一種特殊的二叉樹。這種二叉樹最重要的特徵就是:樹的帶權路徑長度(Weighted Path Length of Tree,簡記為WPL)最小。本文給出了哈弗曼演算法的實現過程,程式碼部分已經描述的比較詳細,這裡就
哈夫曼樹(最優二叉樹)
最優二叉樹,也稱哈夫曼(Haffman)樹,是指對於一組帶有確定權值的葉結點,構造的具有最小帶權路徑長度的二叉樹。 二叉樹的路徑長度則是指由根結點到所有葉結點的路徑長度之和。如果二叉樹中的葉結點都具有一定的權值,則可將這一概念加以推廣。設二叉樹具有n個帶權值的葉結點,那麼從
完成基於哈夫曼樹(最優二叉樹)的壓縮及解壓小程式的收穫
收穫 1) 更有條理的構造我的程式碼了: 先從main方法下手,將自己想要的實現程式的功能以註釋 的方式寫出來,然後再逐漸細化每一部分的功能,每部分的功能都有非常明確的輸入部分,將這些輸入的內容加工,進行輸出(也就是下一部分功能的實現的輸入部分)就是這部分功能
霍夫曼樹(最優二叉樹)簡介
一、霍夫曼編碼 說到霍夫曼樹,就不得不提霍夫曼編碼(Huffman Coding)。霍夫曼編碼是可變字長編碼(VLC)的一種。David.A.Huffman於1952年提出該編碼方法,即完
資料結構實驗之二叉樹六:哈夫曼編碼(SDUT 3345)
題解:離散中的“最小生成樹(最優樹)”。 #include <bits/stdc++.h> using namespace std; void qusort(int l, int r, int a[]) { int x = a[l]; int i = l, j =
哈夫曼編碼(二叉樹+改寫優先佇列)
二叉樹的建立以及優先佇列,前期先對資料進行處理,將所有的字元進行一個頻率的統計,並且記錄在一個結構體指標數組裡面,來進行後續的構建,優先佇列要進行改寫,將其中的比較函式,改寫成最小堆的形式,只需要加入一個引數即可。然後將所有的結構體至今分配空間放入最小堆中,用一箇中間節點去連
轉載:哈夫曼樹的構造和哈夫曼編碼(C++代碼實現)
作者 pos blank 字符 element start man null == 作者:qiqifanqi 原文:http://blog.csdn.net/qiqifanqi/article/details/6038822 #include<stdio.h>
哈夫曼樹與哈夫曼編碼(C語言程式碼實現)
在一般的資料結構的書中,樹的那章後面,著者一般都會介紹一下哈夫曼(HUFFMAN)樹和哈夫曼編碼。哈夫曼編碼是哈夫曼樹的一個應用。哈夫曼編碼應用廣泛,如 JPEG中就應用了哈夫曼編碼。 首先介紹什麼是哈夫曼樹。哈夫曼樹又稱最優二叉樹,是一種帶權路徑長度最短的二叉樹。所謂
踩過無數坑實現的哈夫曼壓縮(JAVA)
最近可能又是閒著沒事幹了,就想做點東西,想著還沒用JAVA弄過資料結構,之前搞過演算法,就試著寫寫哈夫曼壓縮了。 本以為半天就能寫出來,結果,踩了無數坑,花了整整兩天時間!!orz。。。不過這次踩坑,算是又瞭解了不少東西,更覺得在開發中學習是最快的了。 話不多說,進入正題 首先先來講講哈夫曼樹 哈夫曼
QT實現哈夫曼壓縮(多執行緒)
本人菜雞程式設計師一枚,最近剛剛學習的資料結構中的哈夫曼樹,就用QT寫了一個哈夫曼壓縮,話不多說先上步驟,再上程式碼。(如果有更好的想法,歡迎指點) 1.先寫出建最小堆和建哈夫曼樹程式碼(建最小堆的程式碼可以通過STL中的堆代替) 2.寫出壓縮類的程式碼,類中
哈夫曼編碼(2017東北四省賽A題)
給你一個字串,求ASCII編碼多長?哈夫曼編碼多長?求出他們的比值。 比賽的時候沒模板,硬把哈夫曼樹敲了出來,就是不知道哪又bug,然後比賽結束回來,把程式碼打了出來,回來在電腦上一樣的程式碼就過了。 臥槽啊,真是氣死我了! #include <iostream>
哈夫曼編碼(自底向上的哈夫曼編碼)
Description 本題中,讀入n個字元所對應的權值,生成赫夫曼編碼,並依次輸出計算出的每一個赫夫曼編碼。 Input 輸入的第一行包含一個正整數n,表示共有n個字元需要編碼。其中n不超過100。 第二行中有n個用空格隔開的正整數,分別表示n個字元的權值。 Output
Matlab 影象處理-哈夫曼編碼(huffman)
哈夫曼編碼是一種可變長無損編碼,應用範圍廣。這裡介紹利用matalb實現哈夫曼編碼方法。matalb中帶有相關函,下面一一介紹: ENCO = huffmanenco(SIG, DICT) : 哈夫曼
哈夫曼編碼(java)
public class BinaryTree implements Comparable<BinaryTree>{ int key; char data; //左子樹 &n
貪心演算法之哈夫曼編碼(C語言實現)
如題 問題描述:現有一個文字檔案,其中包含的字元資料出現的次數各不相同,先要求對該文字中包含的字元進行編碼,使文字佔用的位數更小。 問題分析 我們知道檔案的儲存都是以二進位制數表示的,如:字元c可以表示為010101…之類的。因 為不同的作業