馬的最短路徑(有障礙)
Problem E 馬的最短路徑
Description
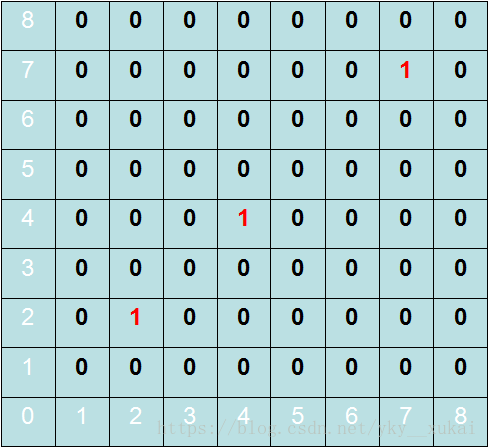
在一個8*8的棋盤上有三個位置馬不能到,它們是(2,2)、(7,7)、(4,4)。棋盤的左下角是(1,1),右上角是(8,8)。給你最初的位置(xs,ys),最終的位置(xe,ye)請程式設計求出馬的最小步數。
Input
有多組測試資料,每組一行,有4個整數,xs,ys,xe,ye。
Ouput
輸出最小步數。
Sample Input
1 1 3 3
Sample Output
5
如圖所示:
實驗程式碼:
#include <iostream> #include <vector> #include <string> #include <algorithm> #include <queue> using namespace std; int direction[8][2] = { { 2, 1 },{ 1, 2 },{ -1, 2 }, { -2, 1 },{ -2, -1 },{ -1, -2 },{ 1, -2 },{ 2, -1 } }; //方向 bool flag[9][9];//標記是否走過 struct Horse { int x; int y; int step; }; int main() { int xs, ys, xe, ye; while (cin >> xs >> ys >> xe >> ye) { struct Horse hs; hs.x = xs; hs.y = ys; hs.step = 0; queue <Horse> lq; lq.push(hs); while (!lq.empty()) { struct Horse hs1; hs1.x = lq.front().x; hs1.y = lq.front().y; hs1.step = lq.front().step; lq.pop(); if (hs1.x == xe && hs1.y == ye) { cout << hs1.step << endl;; } else { for (int z = 0; z < 8; z++) { struct Horse ho; ho.x = hs1.x + direction[z][0]; ho.y = hs1.y + direction[z][1]; ho.step = hs1.step + 1; if (ho.x >= 1 && ho.x <= 8 && ho.y >= 1 && ho.y <= 8 && flag[ho.x][ho.y] == false) { lq.push(ho); flag[ho.x][ho.y] = true; } } } } } return 0; }
相關推薦
馬的最短路徑(有障礙)
Problem E 馬的最短路徑 Description 在一個8*8的棋盤上有三個位置馬不能到,它們是(2,
圖之從一個頂點到其餘各個頂點的最短路徑(有向圖)
目錄 從一個頂點到其餘各個頂點最短路徑的簡介 舉例以及詳細分析 程式碼塊 測試結果 從一個頂點到其餘各個頂點最短路徑的簡介(又名單元最短路徑) 1.定義概覽 Dijkstra(迪傑斯特拉)演算法是典型的單源最短路徑演算法,用於計算一個節點到其他所
有向圖的最短路徑(Floyd演算法)
最近在研究最短路徑演算法,使用java實現。 原始資料是一共有6個點,他們之中任意2個點(i,j)之間的距離v(i,j)的數值如下面二位陣列中所示,整體演算法使用Java語言實現。 class Floyd{ public static void main(S
【ACM】帶權有向圖單源最短路徑(Dijkstra演算法)
最短路徑的第一類問題 求從單個源點到其餘各頂點的最短路徑。這是一種貪心策略,不可以存在負權邊。 演算法簡介 給定帶權有向圖G和源點v0,求從源點v0到G中其餘各頂點的最短路徑。迪傑斯特拉演算法是對
luogu P4779 【模板】單源最短路徑(標準版)
-o2 struct call 哈哈 poi fun fin hole char 線段樹優化dij 哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈 我可能是個智障 // luogu-judger-enable-o2 #pragma GCC diagnostic error "-
[最短路/線段樹大法優化DIJ] 【模板】單源最短路徑(標準版)
洛谷原題 這題我自己看了STL優先佇列後試了試優化DIJ演算法,但我這個菜比只有32分... 還是老老實實用線段樹吧! 自己寫的程式,反正AC了,線段樹大法好! 具體見程式碼 #include<bits/stdc++.h> using namespace std; long lon
最短路徑(鄰接矩陣)(弗洛伊德演算法)
#include<bits/stdc++.h> #define MaxInt 1e8 #define MVNum 100 #define OK 1 #define ERROR 0 using namespace std; typedef int VerTexType; typedef i
單源最短路徑(弱化版)
題目大意: 給出一個有向圖,請輸出從S出發到所有點的最短路徑長度。 解題思路: 看到資料範圍 Spfa 然後int錯了,我就把inf 1099改成了2147483647 一看,dis會炸掉,於是我把dis改成了long long,保險期間,inf
【最短路】洛谷_4779 單源最短路徑(標準版)
題意 給定一個NN個點MM條邊的有向圖,起點是SS,求出起點到每個點的最短路 思路 堆優化過後的dijkstradijkstra演算法。 程式碼 #include<queue&g
#dijkstra+zkw線段樹#洛谷 4779 洛谷 1339 【模板】單源最短路徑(標準版)熱浪
分析 首先為什麼要說這種方法呢,因為根據模板,zkw線段樹優化比STL堆快了一倍,所以說在此推薦我的熱浪題解 程式碼 #include <cstdio> #include <cctype> #include <algorithm> #
題解 P3371 【模板】單源最短路徑(弱化版)
一個story: 2018.10.3,晚上,在與我校是競爭關係的學校的機房(去一起集訓)訓練。 我:(頹) 對方教練:(走過來) 我:(趕快開始假裝研究SPFA) 對方教練:這是?最短路? 我:是啊是啊(瘋狂掩飾尷尬) 對方:這是SPFA? 我:是啊是啊(瘋狂掩
資料結構-基於鄰接矩陣實現圖的遍歷視覺化及使用Floyd、Dijkstra演算法求解最短路徑(JavaScript實現)
使用 JavaScript 基於鄰接矩陣實現了圖的深度、廣度遍歷,以及 Floyd、Dijkstra 演算法求解最短路徑。另外使用 SVG 實現圖的遍歷視覺化。一、輸入首先,輸入資料主要有兩個,一個是存放節點名的陣列,另一個是存放邊物件的陣列。例如://存放圖結點的陣列 va
圖結構練習——最短路徑(Dijkstra演算法)
think: 1注意重複邊的覆蓋 2注意map陣列的初始化 3注意dist陣列的初始化 圖結構練習——最短路徑 Time Limit: 1000MS Memory Limit: 65536KB Problem Description 給定一個
LG4779 【模板】單源最短路徑(標準版)
題意 給定一個 \(N\) 個點,\(M\) 條有向邊的帶非負權圖,請你計算從 \(S\) 出發,到每個點的距離。 資料保證你能從 \(S\) 出發到任意點。 \(1≤N≤100000\); \(1≤M≤200000\); 分析 可以斐波那契堆。 程式碼 #include<iostrea
資料結構-基於鄰接表實現圖的遍歷視覺化及使用Floyd、Dijkstra演算法求解最短路徑(JavaScript實現)
使用 JavaScript 基於鄰接表實現了圖的深度、廣度遍歷,以及 Floyd、Dijkstra 演算法求解最短路徑。另外使用 SVG 實現圖的遍歷視覺化。<!DOCTYPE html> <html lang="en"> <head>
最短路徑(Dijkstra模板)
打一個dj的模板,方便以後查閱 #include <iostream> #include <cstdio> #include <cstring> using na
洛谷 P4779 【模板】單源最短路徑(標準版) 題解
題目來源: 題目描述: 題目背景 狗哥做爛了最短路,突然機智的考了Bosh一道,沒想到把Bosh考住了...你能幫Bosh解決嗎? 他會給你100000000000000000000000000000000000%10金幣w 題目描述 給定n個點的帶權有向
P3371 【模板】單源最短路徑(弱化版)
pre urn mes enable 路徑 gdi name div int // luogu-judger-enable-o2 #include<cstdio> #include<iostream> #include<algorit
拓撲排序+最短路徑(無環加權有向圖最短路徑演算法)
特點: 1、線性時間內解決單點最短路徑問題 2、能夠處理負權邊問題 3、能夠找出最長路徑 不足:因為是基於拓撲排序的,所以不能解決帶環的問題 import java.util.ArrayList; import java.util
資料結構——帶權有向圖(最短路徑演算法Dijkstra演算法)
Dijkstra演算法是由荷蘭電腦科學家艾茲格·迪科斯徹發現的。演算法解決的是有向圖中最短路徑問題。 舉例來說,如果圖中的頂點表示城市,而邊上的權重表示著城市間開車行經的距離。 Dijkstra演算法可以用來找到兩個城市之間的最短路徑。 Dijkstra演算法的輸入包含了一個有權重的有向圖G,以及G中的一個